微尺度效应和壁面滑移对微挤出成型的影响分析

傅志红，罗新桃

（中南大学机电工程学院高性能复杂制造国家重点实验室，湖南 长沙410083）

0 前言

随着现代科学技术的发展，微型产品越来越多。微、小型化成为了当代科技发展的一个重要方向。微机电系统（MEMS）经过十几年的发展，已经成为世界瞩目的重大科技领域之一，并在医疗、信息、汽车工程、自动化等领域得到了应用。

微挤出成型技术［1］作为一种连续成型技术，具有优质、高效、高精度、低成本、适合批量生产等优点，有非常广泛的应用范围，尤其适合长宽比非常大的微器件。塑料异型材挤出是一个复杂的非牛顿黏性流体三维流动过程，型材截面的多样性决定了模具结构也就是挤出口模流道的复杂性，这也使得模具结构对挤出流动影响的分析需要得到更为系统的研究［2］。本文针对微尺度效应、壁面滑移以及口模结构参数，采用挤出数值模拟专用软件Polyflow进行模拟，主要分析这些因素对制品挤出变形的影响。首先，以聚丙烯作为研究对象，确定材料的黏度模型和壁面滑移模型，用Gambit软件分别建立不同压缩段长度下的流道模型并划分网格，用Polyman软件输入所需的材料参数及黏度壁面滑移模型，确定各种边界条件，最后用fluent／post软件得到所需要的结果。

1 微尺度效应

微尺度下，微观组织的形态和变形行为开始对材料的整体行为产生更大的影响，已经超出宏观条件下的连续介质预设，即使在这些简单加载条件下的典型试验中也表现出不同于宏观行为的现象。这种由于材料本身的物理、化学或几何等属性的影响，使得材料在各种微尺度典型性能试验条件下的变形规律表现出不同于宏观典型条件的现象称为材料本征微尺度效应。大量研究［3－5］表明微尺度流动与宏观尺寸流动是有很大区别的。研究发现，水、硅油、酒精和聚合物溶液等在几十微米特征尺寸的微流道中的黏度比正常尺寸下的黏度大50%～80%。这种黏度增大被认为取决于集体分子运动效应或者是固定分子层与固体表面接触。而经典的Navier－Stokes理论与尺寸无关，不能用来解释流动的行为，所以在微挤出成型中，必须要选用合适的黏度模型。常用的黏度模型有Cross模型和Bird－Carreau模型，分别如式（1）和式（2）所示。

式中η0——零剪切黏度，Pa·s

λ——松弛时间，s

n——非牛顿幂律指数

γ——剪切速率，s－1

此外，还有Power模型、Bingham模型以及修正模型等等，对于聚丙烯熔体，黏度低，黏度范围窄，在微尺寸流道中，考虑理想状态剪切率无穷大时，黏度为0后，Bird－Carreau模型更符合材料黏度曲线，因此，本文选用Bird－Carreau模型。

2 壁面滑移

在传统的挤出成型熔体流动分析时，通常假设熔体黏附在通道壁面上，即熔体与通道壁面间的相对速度为0，为无滑移边界条件。然而研究［6］表明，在一定的条件下熔体会沿着壁面滑动，产生壁面滑移。尤其是对于微尺度下聚合物熔体的流动，由于通道的特征尺寸微小，使得熔体流动时的阻力大为增加，成型时需要更大的压力来克服熔体流动时的各种阻力，进而使得熔体在通道壁面处所受剪切应力明显增加，强烈的解缠作用使得大分子之间的相互吸引力减弱，靠近壁面的分子和本体一起移动，壁面滑移对熔体的影响增强。尽管目前对壁面滑移机理的研究还没有形成统一的认识，但人们已对宏观尺度下的壁面滑移模型进行了广泛深入的研究，并建立了广义的Navier滑移模型、极限滑移模型和Uhland管壁滑移模型等多个不同形式的理论模型。Uhland管壁滑移模型通过剪切应力和熔体与管壁之间的摩擦力来求解壁面处的滑移速度，其前提是通道壁面粗糙度对熔体流动的影响是被忽略的［7］。Navier滑移模型、Threshold滑移模型、Asymptotic模型分别如式（3）、（4）、（5）所示。

式中k——滑移系数

e——材料参数

Vr——滑移速度

Vc——临界滑移速度

低黏度的聚丙烯在微挤出成型过程中，熔体速度和壁面滑移速度小、黏度低、壁面阻力小，所以滑移模型本文选用Navier模型。

3 数值模拟

3．1 模型建立

本文以实心椭圆异型材为例，截面尺寸如图1所示，模具结构参数图2所示。由于流道为1／4轴对称图形，所以取其1／4为分析对象。用Pro／E建立模型，保存副本iges文件，然后用gambit导入，划分网格、定义边界条件和区域划分，导出neu文件。其中边界设置如下：入口边界为体积流量Q＝10mm3／s，完全发展流，模型1／4切割面为对称面，即切向应力和法向速度为0，区域1内外侧面为（无）滑移边界，区域2外表面为自由表面，出口边界受力为0。聚丙烯黏度模型采用Bird－Carreau模型［6］：η∞＝0，λ＝0．0032s，n＝0．3292，η0＝99．575Pa·s，滑移模型采用广义的Navier模型：k＝460900，e＝0．5797。

图1 口模尺寸Fig．1 Size of the die

图2 流道结构参数Fig．2 Parameters for the runner

3．2 数值模拟结果及分析

影响异型材微挤出成型的流道参数主要有压缩比、分流角、压缩角、定型段长度等，其他影响因素有挤出速度、挤出温度、冷却水系统、牵引系统等。

本文针对以下两个方面进行模拟：（1）在压缩段长度不变的条件下，壁面滑移边界对熔体流变行为的影响。由于异型材挤出流道复杂而且是非轴对称的，使得压缩段并无固定压缩角，为了便于建模，取压缩段长度为定值（25mm），将主流道过渡到口模短轴的角定义为最大压缩角，过渡到口模长轴的角定义为最小压缩角。异型材挤出流动是一个很复杂的流动过程，尤其是流道的复杂演变过程，而且影响因素的众多性也给分析带来了麻烦，由于只研究固定压缩段长度对熔体流变行为的影响，所以其他参数都设为定值。（2）分析压缩段长度从20～30mm变化时，对制品挤出胀大比的影响，以及不同压缩段长度对应的最大和最小压缩角对制品短轴和长轴最大变形的影响。

以压缩段长度取25mm为例，不考虑壁面滑移与考虑壁面滑移时，流道内沿挤出方向（y方向）的速度场分别如图3（a）和3（b）所示；不考虑壁面滑移与考虑壁面滑移时，流道内的压力场分别如图4（a）和4（b）所示。从图4可知，在通道尺寸和入口流量相同的情况下，有滑移边界条件下的压力小于无滑移边界条件下的压力，无滑移边界的入口压力为3372025Pa，压缩段出口压力为1339421Pa，有壁面滑移边界的入口压力为3371095Pa，压缩段出口压力约1339065Pa，由于尺寸大小相等，可以看出有壁面滑移边界时的压力梯度比无壁面滑移边界的压力梯度小，这可以理解为当变形或应力值达到一定程度时，弹性能释放，导致熔体发生壁面滑移，使壁面处的熔体速度增大，流动阻力减小，通道压力差也随之减小，这说明壁面滑移对流动起到促进作用。

图3 压缩段长度为25mm时的流道速度场Fig．3 Velocity fields in runner with compressive section length of 25mm

图4 压缩段长度为25mm时的流道压力场Fig．4 Pressure fields in runner with compressive section length of 25mm

同样以压缩段长度取25mm为例，不同条件下口模出口处长轴方向（x方向）的速度分布如图5所示，短轴方向（z方向）的速度分布图6所示。由图5和图6可以看出，壁面滑移对法向速度的分布均匀性也是有影响的。

图5 口模出口处x方向速度分布图Fig．5 Velocity distribution along x－axis at outlet of die

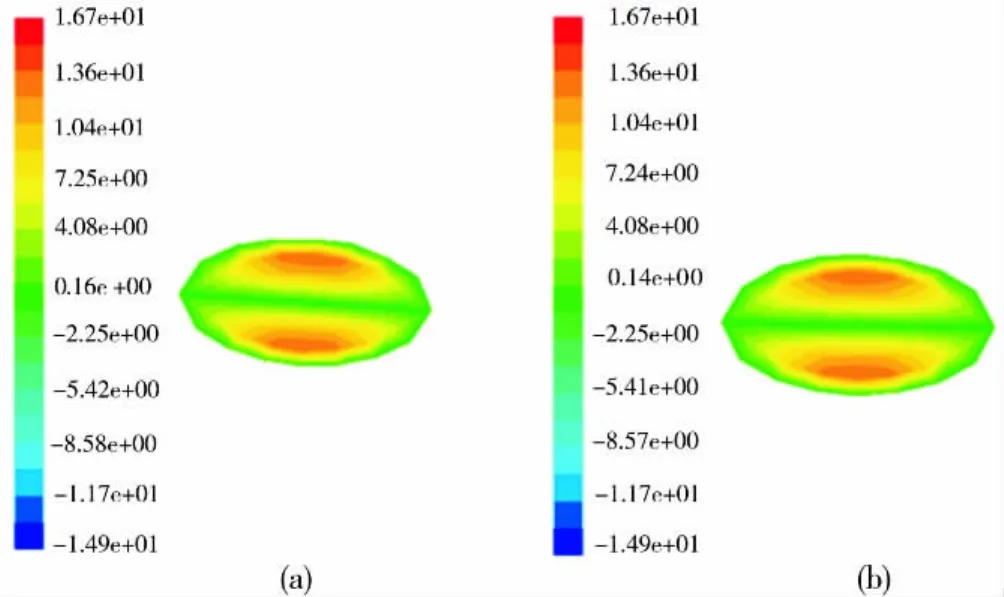
图6 口模出口处z方向速度分布图Fig．6 Velocity distribution along z－axis at outlet of die

图7和图8为fluent／post里面输出最大速度值。由图可知，不考虑壁面滑移时，口模出口处x方向的最大速度Vxmax1＝11．503981mm／s，z方向的最大速度Vzmax1＝13．418581mm／s，考虑壁面滑移条件下口模出口处x方向的最大速度为Vxmax2＝11．496246mm／s，z方向上的最大速度为Vzmax2＝13．405548mm／s。可以看出口模出口处的速度分布很不均匀，Vz主要分布在左右对称区域，Vx主要分布在上下对称区域，而且Vzmax大于Vxmax，尤其是Vz随坐标的变化很大。经过初步计算，Vz随z轴坐标变化的最大变化率约每毫米134mm／s，Vx随x轴坐标变化的最大变化率约每毫米57．5mm／s。从有无壁面滑移条件下x、z轴方向的最大速度对比可知，虽然壁面滑移速度较小，但是也使最大速度减小，速度变化减小，对速度分布均匀性起着促进作用。

图7 不考虑壁面滑移时Vz随短轴坐标变化曲线Fig．7 Changes of Vzalong z－axis without wall slipping

图8 不考虑壁面滑移时Vx随长轴坐标变化曲线Fig．8 Changes of Vxalong x－axis without wall slipping

由图9可大致看出制品截面的变形情况。再根据不同压缩段长度下由matlab统计数据得出图10。由图10可知，对于同尺寸下比较有无壁面滑移边界得到的数据可知，壁面滑移条件下变形稍小，这也说明壁面滑移对流动起到促进作用，流动均匀性稍有改善，变形减小，而且压缩段长度在20～30mm之间时，挤出胀大比随压缩段长度的增加而减小，即随压缩角的减小而减小。

由压缩角的定义可知：最大压缩角αmax＝2×（2．4－0．3）／L，最小压缩角αmin＝2×（2．4－0．6）／L，L为压缩段长度，于是可计算得出压缩段长度与对应压缩角关系如表1所示。

由图11和12可知，在压缩比、定型段长度等相同的条件下，最大变形随着压缩角的变大而变大，而且在有壁面滑移边界条件下的变形小于无壁面滑移边界条件下的变形。

图9 节点位置变化图Fig．9 The node positions

图10 挤出胀大比随压缩段长度变化曲线Fig．10 Dependence of die swell ratio on length of compressive section

表1 压缩段长度与对应的压缩角Tab．1 The length of compressive section and corresponding compressive angles

图11 短轴最大变形随最大压缩角变化曲线Fig．11 Dependence of maximumdeformation along z－axis onαmax

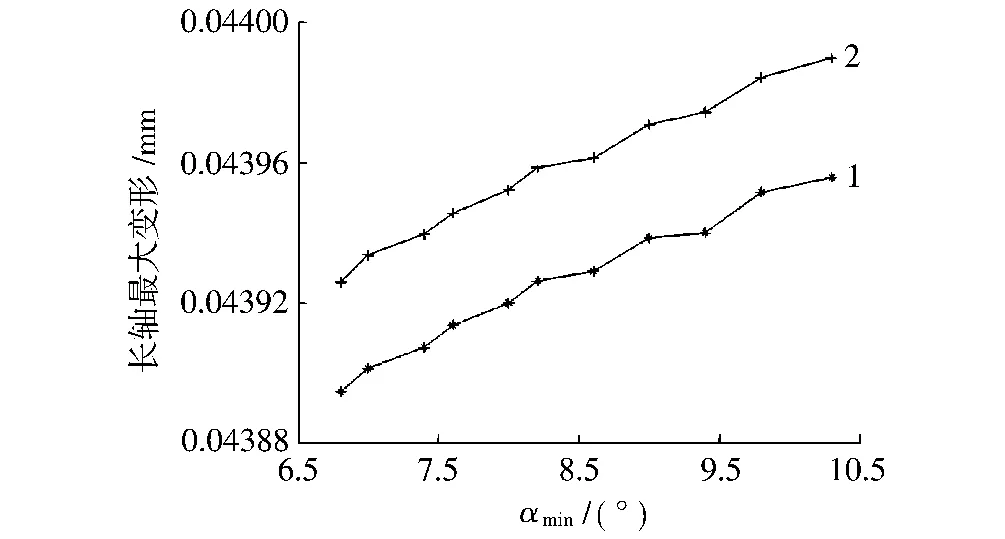
图12 长轴最大变形随最小压缩角变化曲线Fig．12 Dependence of maximumdeformation along x－axis onαmin

4 结论

（1）有壁面滑移条件下流道入口压力和出口压力均比无壁面滑移条件下小，且壁面滑移条件下入出口压力梯度比无壁面滑移条件下小，表明壁面滑移使熔体流动阻力减小，起到促进流动的作用；

（2）通过分析口模出口处长轴和短轴方向速度场可知，出口处速度极不均匀，有壁面滑移条件下速度最大值和速度随坐标变化率均比无壁面滑移条件下小，表明壁面滑移对速度分布均匀性起促进作用；

（3）在其他参数均为定值的情况下，通过对压缩段长度为20～30mm区间离散数值模拟结果表明，制品变形随压缩角变小而变小，同时有壁面滑移条件下变形比无壁面滑移条件下小；

（4）通过数值模拟壁面滑移对流动过程中的压力、速度和变形的影响发现，速度均匀性是影响变形的主要因素，口模出口处短轴方向速度随坐标变化大，变形大。

［1］ 徐 斌．微尺度效应对聚合物熔体壁面滑移影响的研究［J］．材料工程，2008，（10）：16－20．Xu Bin．Study on Micro－scale Effect on Impact of Polymer Melt Wall Slip［J］．Materials Engineering，2008，（10）：16－20．

［2］ 刘 斌．流道结构对塑料挤出流动影响数值分析［J］．大连理工大学学报，2003，43（4）：442－446．Liu Bin．Numerical Analysis of Effect of Channel Structure on Plastic Extrusion Flow［J］．Journal of Dalian University of Technology，2003，43（4）：442－446．

［3］ Yao Donggang，Byung Kim．Simulation of the Filling Process in Micro Channels for Polymeric Materials［J］．Journal of Micromechanics and Microengineering，2002，（12）：604－610．

［4］ Israelachvili J N．Measurement of the Viscosity of Liquids in Very Thin Films［J］．J Colloid Interface Sci，1986，110：263－271．

［5］ Eringen A C，Okada K．A Lubrication The ory for Fluids with Microstructure［J］．Int J Eng Sci，1995，33：2297－2308．

［6］ 邹 健．压缩角对双腔微管挤出流动均匀性的数值模拟与分析［J］．模具制造，2010，（4）：1－5．Zou Jian．Numerical Simulation and Analysis of the Effects of Compression Angle on FlowUniformity of Double－chamber Micro－tube［J］． Mold Manufacturing，2010，（4）：1－5．

［7］ 唐 俊．考虑熔体弹性的壁面滑移对微尺度流动的影响［J］．中国机械工程，2009，20（11）：1361－1364．Tang Jun．Study on the Effect of Wall Slip on the Microscale FlowConsidering Melt Elasticity［J］．Chinese Journal of Mechanical Engineering，2009，20（11）：1361－1364．