电力流向及规模优化研究模型和研究方法

2012-02-08孙珂张琳宋福龙孙英云肖笋

电力建设 2012年8期

孙珂，张琳，宋福龙，孙英云，肖笋

(1.国网北京经济技术研究院，北京市 100052;2.华北电力大学电气与电子工程学院，北京市 102206)

0 引言

电力流向与能源资源分布、能源流向、国家能源政策、区域经济发展、地区电价水平等因素密切相关。美国、欧盟地区能源资源的分布与负荷分布较为匹配，电力流向主要呈就地平衡模式，目前未出现大规模的电力流动。与之不同的是，我国能源资源与负荷需求呈逆向分布，导致我国电力出现“西电东送”、“南电北送”大规模电力流向。

在以往的电力流向及规模的确定中，常用的方法是在确定电源基地送电能力和受端市场空间的基础上，依据送电通道的输电能力，参考专家经验，确定各电源基地的送出规模和送电方向［1-3］。这种判断方式具有一定的合理性，能够保证电力流向及规模的结果是一个可行解，但无法回答是否为最优解问题。因此，需要建立明确的目标函数，对电力流向及规模进行数学优化。本文考虑影响电力流向及规模的因素，围绕优化目标的确定、目标函数的建立、限制条件的选取、优化问题的数学解析及结果分析为主线，对未来我国电力流向及规模进行优化。

1 基于电力流向及规模优化的电力传输模型

1.1 模型描述

电力流向问题的实质是研究如何把电力从能源基地送往负荷中心，并满足技术、经济上的要求。其模型可抽象为:假设在电力网络内具有M个送端，N个受端，每个送端均可向不同受端输送电力。为简化模型，考虑送端与受端之间的电力传送，不考虑各受端之间的电力中转。电力传输网络的简化模型如图1所示。图中:B1～BM为M个能源基地，作为送端;D1～DN为N个负荷中心，作为受端;Qi为能源基地Bi的发电装机容量，i=1，2，…，M;Sj为负荷中心Dj的市场空间，j=1，2，…，N;Lij为能源基地Bi到负荷中心Dj的距离;Pij为由能源基地Bi送往负荷中心Dj的电力。

图1 电力传输网络的简化模型Fig.1Simplified model of power transmission network

1.2 模型约束条件

在实际电网中，各能源基地的出力不可能大于其装机总容量，从相同能源基地出发的所有线路传输功率总和不能多于该能源基地的装机容量，送往相同负荷中心的所有线路输送功率总和不能高于该负荷中心的受电空间。此外，由于负荷中心不得向能源基地反送电力，因此所有线路的输送功率均为正值;考虑我国电力“北电南送”、“西电东送”的实际电力流向，依据能源基地与负荷中心的相对位置，违背整体电力流向的送电模式不存在。例如西南水电不向华北送电，即Pef=0。所以，各参数需满足以下约束条件

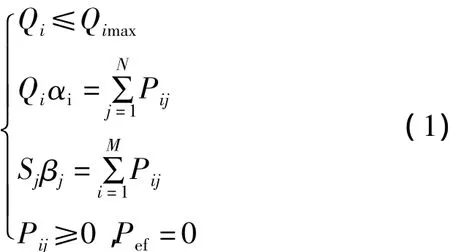
式中:Qimax为能源基地Bi的最大装机能力;αi为能源基地Bi的装机出力系数;βj为负荷中心Dj的外受电系数。

各参数的计算方法为:

(1)根据能源资源可支撑最大装机水平和装机规划情况，确定能源基地Bi的装机规模Qi。

(2)αi与装机类型有关。一般，火电的αi为0.92，水电的αi为0.67［4-6］，风电的αi为0.5［7-9］。

(3)通过各负荷中心电力需求预测结果和本地已核准装机情况，进行电力电量平衡计算，得到负荷中心Dj的市场空间Sj。

(4)考虑负荷中心通过本地建电源满足25%～30%的用电需要，βj一般为70%～75%［10-11］。

2 电力流向及规模优化目标函数

2.1 电力传输成本最小

从电网规划的技术经济评价角度来看，电力流向优化作为电网规划的一部分，其最终目标也应为经济性最好。在经济评价中，常用的方法为年费用最小法，即以整个输电网络每年产生的费用最小为目标。

电力传输成本最小法是以总输电年费用最小为目标的电力流向优化方法，即从能源基地Bi向负荷中心Dj的输电总费用为

式中:Cbase，ij为从能源基地Bi向负荷中心Dj送电的投资年值;Cwast，ij为从能源基地Bi向负荷中心Dj送电的年损耗费用;Coperate，ij为从能源基地Bi向负荷中心Dj送电的年运行费用;Cother，ij为从能源基地Bi向负荷中心Dj送电的其他费用。且有

式中:cij为初投资，cij=ηijPijLij，ηij为输电工程的单位容量、单位距离投资;γ为折现率;T为运营期;δij为运行维护费率;λ为环保系数。

因直流输电的损耗包括线路损耗和换流站损耗，而交流输电的损耗仅为线路损耗，则有

式中:vi为能源基地Bi的标杆上网电价;τij为利用小时数;μij为交流线路损耗系数(线损);μx-ij为直流线路线路损耗系数(线损)，μh-ij为直流线路换流站损耗系数(换损)。

因此，基于电力传输成本最小的电力流向及规模优化目标函数为

2.2 电价竞争力最大

将能源基地电力送至受端负荷中心的电价与本地建厂发电的上网电价之差是较为明确的，且容易被大众接受的评价标准。电价差越大，代表该输电方式电价竞争力越大，有利于抑制电价上涨，具有更好的社会效益。因此，可以考虑以电价竞争力最大为目标，进行电力流向优化。

电价竞争力最大法是以受端上网电价与到网电价差的总和最大为目标的电力优化方法，其目标函数为

式中:Fj为负荷中心Dj的火电标杆上网电价;Ei为能源基地Bi的标杆上网电价;Mij为将容量Pij的电力从能源基地Bi送至负荷中心Dj的输电价(含损耗电价)，主要影响因素有工程造价、输电量、输电损耗等。

电力从能源基地Bi送至负荷中心Dj往往具有多种输电方式和多个工程，其输电价是各项工程输电价的和，不能用统一的公式和几个固定参数计算。但工程造价、输电损耗、输电量等因素对于输电价的影响趋势是一致的，因此，考虑简化输电价模型，用以代表输电价的相对大小。考虑各参数之间的关系，输电价简化为

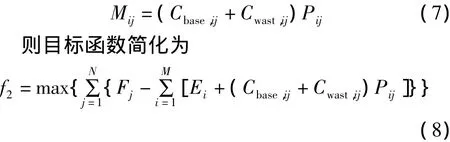
2.3 综合目标函数

综合电力传输成本最小及电价竞争力最大目标函数，得到电力流向及规模优化的综合目标函数为

3 我国电力流向及规模优化计算分析

3.1 优化计算经济指标及参数

(1)输电距离。通过初步估算，各大型水、火、风电基地到华北、华中、华东负荷中心的距离及送电方式选择如表1所示。

表1 大型能源基地至负荷中心送电距离及送电方式Tab.1Transmission mode and distance from power base to load center

(2)交直流送电模型及参数。交流输电采用“点对网”送电模型，在双回线路送电9 GW·h，考虑送端电厂通过1 000 kV线路直接接入，送端设开关站;受端设变电站，加装3×3 GW主变;每300 km建设1个变电站，加装3×3 GW主变。具体的投资参数为:①送端开关站投资7.57亿元;②中间变电站规模3×3 GW，投资22亿元;③受端变电站规模3× 3 GW，投资17.39亿元［12-16］。

(3)直流输电参数如表2所示。

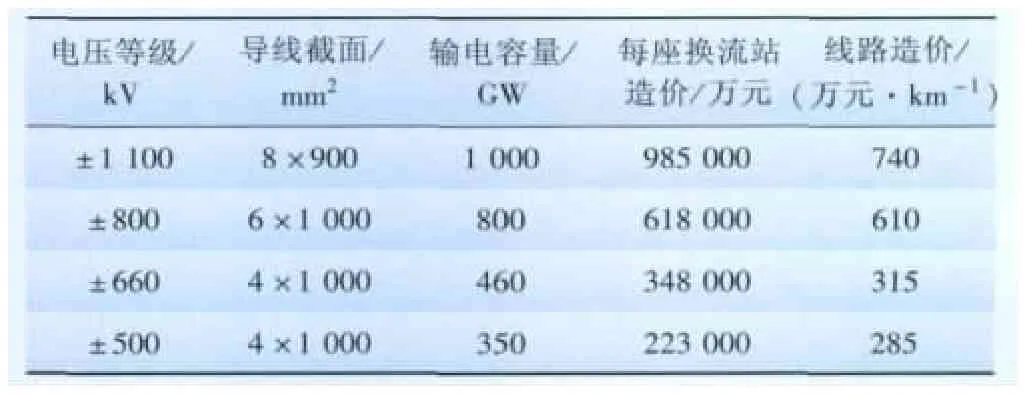
表2 直流输电投资参数Tab.2Investment parameters of DC transmission

(4)年费用计算参数如表3所示。

表3 年费用计算基本参数Tab.3Calculation parameters of annual fee

3.2 电力流向优化结果分析

3.2.1 2020年电力流向优化结果

采用上述电力流向及规模优化方法，得到2020年我国电力流向优化结果如图2。

华北电网负荷中心距离北部的煤电、风电基地距离较近，其外受电力主要考虑来自距离其较近的能源基地，包括锡盟、蒙西、呼盟、宁东、陕北、山西能源基地。此外，宝清能源基地距离华北电网相对于华中、华东电网更近，按照就近消纳的原则，同样考虑送入华北电网。

图2 2020年我国电力流向Fig.2China power flow in 2020

华中电网位于华北、华中、华东(“三华”)电网的枢纽位置，一方面其与西北部煤电基地的距离远远小于与华东电网的距离，另一方面，华中电网的湖北等省份水电装机较多。考虑水火互济原则，新疆的哈密、伊犁、准东及西北陇东、彬长等能源基地的火电、风电送入华中电网，提高电网运行经济性。此外，为满足华中负荷中心的用电需要，结合我国“西电东送”的整体电力流向，部分四川水电和金沙江水电也考虑送至华中东四省消纳，部分通过山西等附近的能源基地补充。

华东电网通过直流线路接受来自金沙江、酒泉、锡盟、蒙西、赤峰能源基地电力，充分发挥直流线路远距离送电的经济优势。锡盟、宁东、陕西、山西部分电力通过交流通道接递送至华东。

3.2.2 2015年电力流向优化结果

2015年我国电力流向如图3所示。与2020年优化结果相对照，2015年电力流向优化结果基本可以实现网架的合理过渡。

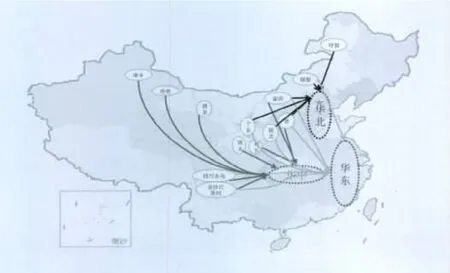
图3 2015年我国电力流向计算结果Fig.3Calculation results of China power flow in 2015

4 结论

本文综合考虑影响电力流向及规模的各个因素，从电力建设成本最小化以及电价竞争力最大化的角度探讨了电力流向及规模。确定了优化目标、建立了目标函数、设定了限制条件，同时介绍了求解优化问题的数学解析方法并对结果进行了深入的分析，以此对未来我国电力流向及规模进行了优化研究。结果表明未来我国电力将由西北流向华中，西南水电流向华中和华东，北方煤电就近送往华北，部分富余电力送往华东，整体呈现“西电东送”、“北电南送”的格局。

［1］潘雄.电网优化规划方法研究［D］.重庆:重庆大学，2002:11-13.

［2］苏建设，陈陈.电网灵活规划研究综述［J］.华东电力，2001，29 (1):7-9.

［3］谭忠富.电力成本综合优化的系统学方法研究:优化规划［J］.现代电力，2001，18(2):90-97.

［4］孟祥萍，谭万禹，杨秀霞.影响发电机组等效可用系数的因素分析［J］.吉林电力技术，1998(2):1-4.

［5］刘雄.发电设备可靠性指标分析及预测［D］.北京:华北电力大学，2010:26-45.

［6］郭永基.电力系统及电力设备的可靠性［J］.电力系统自动化，2001，25(17):53-56.

［7］孙永全，郭建英，陈洪科，等.兆瓦级直驱风力发电机组可靠性增长预测［J］.中国电机工程学报，2010，30(18):67-71.

［8］栗文义，张保会，巴根.风能大规模利用对电力系统可靠性的影响［J］.中国电机工程学报，2008，28(1):100-105.

［9］吴义纯，丁明.基于蒙特卡罗仿真的风力发电系统可靠性评价［J］.电力自动化设备，2004，24(12):70-73.

［10］鞠平.电力系统负荷建模理论与实践［J］.电力系统自动化，1999，23(19):1-6.

［11］鞠平，戴琦，黄永皓，等.我国电力负荷建模工作的若干建议［J］.电力系统自动化，2004，28(16):8-11.

［12］刘万东，郑晓广，李君章.特高压线路施工新技术的应用［J］.电网技术，2009，32(10):68-73.