A Modified Differential Evolution for Uniform Parallel Machines Scheduling Problem with Minimizing Makespan

NIU Qun(牛 群)，ZENG Ting-ting(曾婷婷)，ZHOU Zhuo(周 卓)

Shanghai Key Laboratory of Power Station，School of Mechatronic Engineering and Automation，Shanghai University，Shanghai 200072，China

Introduction

The problem of scheduling n jobs on m uniform parallel machines with the objective ofminimizing makespan is considered，which is denoted as Qm‖Cmax［1］.The uniform parallel machine scheduling problem(UPMSP)is known to be non-deterministic polynomial-time(N)hard even for m=2［2，3］.In the modern manufacturing environment，the UPMSPs are fundamental to various complex real-life applications.Although a number of researches have been devoted to the UPMSP，such as the semiconductor manufacturing［4］and the flexible resource filed［5］，which has received a great deal of attention in the academic and engineering circle［6］，there have been few reports on uniform parallel machines.

Owing to the challenge of the UPMSP，some traditional heuristic algorithms，such as largest processing time(LPT)and EDD(earliest due date first)［7-9］，have been developed to solve this problem. Koulamas et al.［10］showed that an extension of the SPT and LPT rule for UPMSP with minimizing makespan.Burkard et al.［11］considered minimization makespan for UPMSP with MULTIFIT algorithm.However，it is difficult to achieve an optimal solution since these methods are suitable only for small scale problems and no single dispatching rule guarantees good result in various problems［12］.

In recent years， computational intelligence-based techniques such asgeneticalgorithms(GA)，simulated annealing(SA)，and particle swarm optimization(PSO)have been successfully used to solve the scheduling problems.Liu et al.［13］combined GA with SA for minimizing the makespan in identical parallel machine scheduling problems.Damodaran et al.［14］used GA to minimize the makespan of identical parallel machines.Lee et al.［15］addressed a makespan minimization scheduling problem on identical parallel machines using SA.Sivasankaran et al.［16］presented design and comparison of SA and greedy randomized adaptive search procedure to minimize the makespan on unrelated parallel machines.Wang et al.［17］employed PSO to minimize the makespan for parallel machines with non-identical job sizes. In the literatures，researchers mainly focus on the identical parallel machine scheduling problem，however，the uniform parallel machines obtain few attention.Balin［18］proposed a new crossover operator and a new optimality criterion so as to adapt GA to non-identical parallelmachine scheduling problem.The meta-heuristic algorithms above outperform the traditional heuristic algorithms in terms of quality and execution time for a large number of jobs.

Differential evolution(DE)，proposed by Storn and Price［19］，is a simple yet powerful evolutionary algorithm for solving nonlinear， non-differentiable， and multi-modal optimization problems.Since DE is simple to implement and needs little tuning on its parameters，it has been successfully employed to solve various optimization problems such as electrical power distribution［20］，environmental science［21］，and medical science［22］.

In this paper，we propose a modified differential evolution(MDE)，which takes out the mutation operation and introduces roulette wheel selection strategy intoDE.Roulette wheel selection strategy is used to avoid the loss of effective gene，and it willprovide higherprobability to higherperformance individuals to survive.The improvement can enhance global convergence and calculation accuracy.To test the performance of MDE，162 randomly generated instances are conducted using several popular methods，including DE，GA，and SA.

The rest of the paper is organized as follows.Firstly，the UPMSP is mathematically formulated.Secondly，it deliberates the MDE method.To demonstrate the performance of the optimization algorithm，the experiment conducted on a random set of instances is presented in the following section，the computation resultsand comparisons are also described.Finally，the conclusion is presented.

1 Problem Description

Consider a makespan minimization problem on m uniform parallel machines(Mi，i=1，2，… ，m)，where Mihas a speed viand can process only one job at a time.There are n jobs(Jj，j=1，2，… ，n)，ready to be processed without interruption at time zero.If Jjwhich has a processing requirement of pjon Miis processed，it will require pj/vitime units to complete.Without loss ofgenerality，it is assumed that the job processing requirements are integers.Notations are given as follows.

n is the total number of jobs waiting to be processed.

m is the total number of machines available to process the jobs above.

i is the index of machine，i=1，2，… ，m.

j is the index of job，j=1，2，… ，n.

viis the speed of each machine.

p(i，j)is the processing time of job j，j∈n at machine i，i∈m.

Processing time of a job j on different machines can be expressed by the following equation:

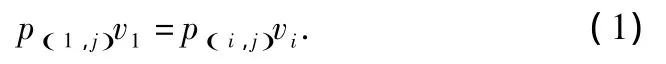
The maximum completion time(makespan)is equal to:

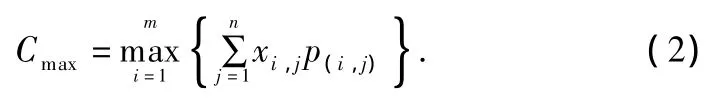
Thus，the objective function can be formulated as follows:

2 The Proposed MDE

2.1 Brief overview to classical DE algorithm

DE is a population-based stochastic parallel direct search method that utilizes concepts borrowed from the broad class of evolution algorithms.This technique combines simple arithmetic operators with classical events of crossover，mutation，and selection to evolve from randomly generated initial population to final individual solution.The key idea behind DE is a scheme for generating trial parameter vectors.The main procedures of the classical DE include:(1)initialization;(2)mutation and crossover operation，used to generate new vectors(trial vectors);(3)selection operation，determines which of the vectors will survive the next generation;(4)repeat steps(2)and(3).

2.2 MDE

The effect of mutation operation in DE algorithm is to overcome the premature convergence and increase diversity of the population.In the update processing of DE，the huge changes of population have an undesirable effect on the results，therefore，we propose a modified DE，namely MDE，which cancels the mutation operation and introduces the roulette wheel selection strategy.Roulette wheel selection strategy is used to avoid the loss of effective gene and provide more probability for potential individuals to survive.Meanwhile it removes the control factor，which can simplify the conventional DE.The MDE can enhance global convergence and calculation accuracy.Figure 1 shows the procedure of the MDE.

Fig.1 Flowchart of the MDE algorithm

2.3 Procedure of MDE

2.3.1 Encoding

There are several types of solution representation for UPMSP.AsDE issuitable forcontinuousoptimization problems，the real number encoding method is adopted in this paper［23］.For a UPMSP with n jobs and m uniform parallel machines，n real numbers are randomly generated from a uniform distribution between［1，m+1).In terms of the value in the solution，the integer part of the real number represents the machine that the job is assigned，and the fractional part stands for the processing order of jobs on each machine.Figure 2 illustrates the solution representation of nine jobs on four uniform parallel machines.

Fig.2 Solution representation

2.3.2 Initial population

The initial populations are created randomly and attempt to cover the entire parameter space uniformly.Uniform probability distribution for all random variables is assumed，that is:

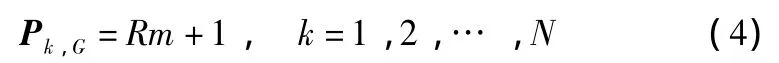
where R is a random number between 0 and 1.Several initial vectors can be obtained by repeating the same operation.Members of the initial vectors are the parents of the next generations and the efficiency ofthe algorithm is highly dependent on their“quality”.

2.3.3 Roulette wheel selection strategy

In this paper，the solution obtained from makespan value determined the fitness of each individual.To get the better solution，makespan value should be as small as possible.The roulette wheel selection strategy is widely used in GA to select a relative better solution based on their fitness value.Selection probability(ps)of the kth individual is calculated as follows:

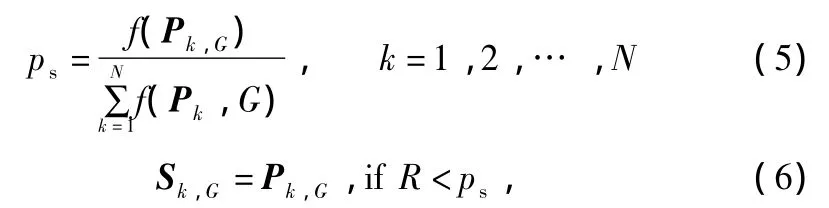
where f(Pk，G)denotes fitness of Pk，G，Sk，Gis a selection vector of the kth individual，and N is the population size.

Selection vectors with higher fitness value will have a higher probability to be selected toembed intothe next generation.The main purpose of this roulette wheel selection strategy is to preserve the good ones and eliminate the bad individuals from parent generation to offspring.

2.3.4 Crossover operation

To increase the diversity ofthe perturbed parameter vectors，crossover is introduced.The target vector is mixed with the selection vector，using the following scheme，to yield the trial vector Uk，G+1=(uk，1，G+1，uk，2，G+1，… ，uk，D，G+1)，that is:

where R(j)is the jth evaluation of a uniform random number generator between 0 and 1.C is the crossover constant between 0 and 1，which has to be determined by the user.r(k)is a randomly chosen index from 1，2，… ，D which ensures that Uk，G+1gets at least one parameter from Sk，G+1.Otherwise，no new parent vector would be produced and the population would not alter.

2.3.5 Greedy selection

To decide whether or not it should become a member of the next generation(G+1)，the trial vector Uk，G+1is compared with the target vector Pk，Gusing the greedy criterion.Assume that the following objective function is to be minimized.

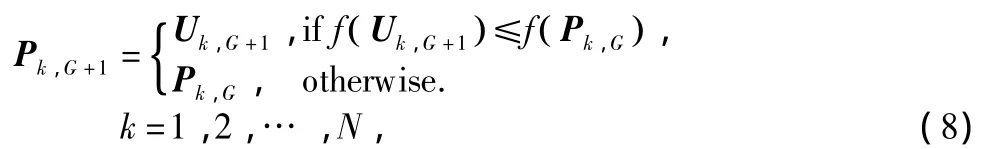
Once the current population is updated，it evolves again through Roulette wheel selection strategy，crossover，and greedy selection until the optimum is located，or a predefined termination criterion is reached.

3 Computational Results

In this section，162 sets ofrandom instances are generated［7，8］to evaluate the performance of the proposed MDE.The computational results are compared with other four approaches including LPT dispatching rule，DE，GA，and SA.All the procedures in this paper are implemented by using the Matlab software and running on a PC with a Pentium(R)Dual 1.6 GHz processor with 2 GB of RAM.

3.1 Data generation

In the experiments，the following fourfactors are considered:number of machines m，number of jobs n，machine speeds vi，and job processing requirements p(i，j).Nine values of n tested are 10，15，20，25，30，50，100，500，and 1 000，and two values of m tested are 3 and 5.The machine speeds are randomly generated from a uniform distribution T(1，v)with v=3，5，7，and the values are rounded off to three decimal places.The job processing requirements are randomly generated from a discrete uniform distribution d(1，b)with b=25，50，100.For instance，the notation of j10m3p25v3 means 10 jobs，3 machines，25 processing time，and 3 machines speeds.The combinations of the four factors give a total of 162 sets of problems.

3.2 Parameter setting

Selecting the appropriate values for the parameter set in DE plays an important role in obtaining better solutions for the optimization problems.In conventional DE，there are two parameters，F controls the speed of the search and C controls the crossover operation.Since MDE introduces the roulette wheel selection operator instead of mutation operator，only one parameter C needs to be investigated.Five randomly generated instances are tested by varying C∈［0.1，1.0］with a step size of 0.1 for each.

In each experiment，the population size is set to 20，and the number of generations(G)is set to 400.Thirty independent runs are performed on each instance.Table 1 shows the comparison of MDE in terms of different values of C，and the value denotes the best result among thirty runs.

Table 1 Comparison of MDE in terms of different values of C

From Table 1，the results obtained by MDE are different under different values of C.When C=0.2，the results are better than other values.Therefore，C in MDE is determined with C=0.2 in the following experiments.

3.3 Implementation and simulation results on 162 instances

To verify the effectiveness of MDE，experiments are conducted to make a comparison with conventional DE，GA，and SA.All the algorithms run thirty times on each instance，with the following settings:PS=20，G=400，where PSdenotes population size. ForGA，single-pointcrossover operation and swap mutation operation are adopted.The crossover rate and the mutation rate are set to 0.8 and 0.1.For SA，initial temperature T0=0.6 and cooling rate P0=0.95.In Tables 2 and 3，“Best”denotes the best makespan found over thirty runs，“Average”expresses the average makespan，and“Time”means CPU average time.Tables 2 and 3 summarize the comparison results obtained by LPT，MDE，DE，GA，and SA.Each table consists of 81 instances.It is clear that，as to small scale instances，MDE has similar results with DE in terms of best makespan while it outperforms DE in average makespan.The results also show that the best and average makespans obtained from MDE are betterthan othermeta-heuristic algorithms，such as DE，GA，and SA.Furthermore，MDE approach shows great performance in terms of large scale instances.Note that in all instances，the computational time reported here using MDE is comparatively less than other four algorithms.

Table 2 Comparison of the five algorithms with different jobs on three uniform parallel machines

(Table 2 continued)

Table 3 Comparison of the five algorithms with different jobs on five uniform parallel machines

(Table 3 continued)

(Table 3 continued)

In Table 4，the detailed comparison among the four algorithms is given.For all problems，MDE can get better values on 80 instances compared with DE while there are 82 instances equal with DE.However，GA and SA cannot obtain this superior trend when compared with DE.In particular，there are 17 instances for GA and 31 instances for SA worse than DE.Therefore，MDE appears more effective than DE，GA，and SA.

Table 4 The performances of MDE，GA，SA，and DE

4 Conclusions

A modified DE is proposed to solve the UPMSP.Due to the reasonable combination of the DE search and roulette wheel selection strategy，MDE can produce satisfactory solutions compared with the conventional DE.Computational simulations demonstrate the effectiveness and efficiency of MDE.The performance of MDE is evaluated in comparison with DE，GA，and SA on 162 random instances.The results clearly confirm that MDE substantially outperforms DE，GA，and SA for all the instances. MDE outperforms most ofthe LPT solutions.Therefore，MDE is an effective and competitive method for the UPMSP.

In the scope of future work，a further interesting issue is extending MDE to more complex scheduling problems such as hybrid flow shop scheduling.

［1］Graham R L，Lawler E L，Lenstra J K，et al.Optimization and Approximation in Deterministic Sequencing and Scheduling:a Survey［J］.Annals of Discrete Mathematics，1979，5(2):287-326.

［2］Lenstra J K，Rinnooy K A H G.Complexity of Scheduling under Precedence Constraints［J］.Operations Research，1978，26(1):22-35.

［3］Sethi R.On the Complexity of Mean Flow Time Scheduling［J］.Mathematics of Operations Research，1977，2(4):320-330.

［4］Dessouky M M.Scheduling Identical Jobs with Unequal Ready Times on Uniform Parallel Machines to Minimize the Maximum Lateness［J］.Computers and Industrial Engineering，1998，34(4):793-806.

［5］Ruiz-Torres A J，López F J，Ho J C. Scheduling Uniform Parallel Machines Subject to a Secondary Resource to Minimize the Number of Tardy Jobs［J］.European Journal of Operational Research，2007，179(2):302-315.

［6］Liu M，Wu C.Scheduling Algorithm Based on Evolutionary Computing in Identical Parallel Machine Production Line［J］.Robotics and Computer-Integrated Manufacturing，2003，19(5):401-407.

［7］Liao C J，Liao C H.Makespan Minimization for Two Uniform Parallel Machines［J］.International Journal of Production Economics，2003，84(2):205-213.

［8］Lin C H，Liao C J.Makespan Minimization for Multiple Uniform Machines［J］.Computers ＆ Industrial Engineering，2008，54(4):983-992.

［9］Wu C C，Lee W C，Chen T.Heuristic Algorithms for Solving theMaximum LatenessScheduling Problem with Learning Considerations［J］.Computers ＆ Industrial Engineering，2007，52(1):124-132.

［10］Koulamas C，Kyparisis G J.A Modified LPT Algorithm for the Two Parallel Machine Makespan Minimization Problem［J］.European Journal of Operational Research，2009，196(1):61-68.

［11］Burkard R E，He Y.A Note on MULTIFIT Scheduling for Uniform Machines［J］.Computing，1998，61(3):277-283.

［12］Liu M，Wu C. A Genetic Algorithm forMinimizing the Makespan in the Case of Scheduling Identical Parallel Machines［J］.Artificial Intelligence in Engineering，1999，13(4):399-403.

［13］Liu M，Wu C.Identical Parallel Machine Scheduling Problem for Minimizing the Makespan Using Genetic Algorithm Combined with Simulated Annealing［J］.Chinese Journal of Electronics，1998，7(4):317-321.

［14］Damodaran P，Hirani N S，Velez-Gallego M C.Scheduling IdenticalParallelBatch Processing Machines to Minimise Makespan Using Genetic Algorithms［J］.European Journal of Industrial Engineering，2009，3(2):187-206.

［15］Lee W C，Wu C C，Chen P.A Simulated Annealing Approach to Makespan Minimization on Identical Parallel Machines［J］.The International Journal of Advanced Manufacturing Technology，2006，31(3/4):328-334.

［16］Sivasankaran P，Sornakumar T，Panneerselvam R.Design and Comparison of Simulated Annealing Algorithm and GRASP to Minimize Makespan in Single Machine Scheduling with Unrelated Parallel Machines［J］. Intelligent Information Management，2010，2(7):406-416.

［17］Wang Y，Chen H P，Shao H.Minimizing Makespan for Parallel Batch Processing Machines with Non-identical Job Sizes Using Quantum-Behaved Particle Swarm Optimization［C］.The 4th International Conference on Intelligent System and Knowledge Engineering，Hasselt，Belgium，2009:32-39.

［18］Balin S.Non-identical Parallel Machine Scheduling Using Genetic Algorithm［J］.Expert Systems with Applications，2011，38(6):6814-6821.

［19］Storn R，Price K V.Differential Evolution:a Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces［J］.Journal of Global Optimization，1997，11(4):341-359.

［20］Chang T T，Chang H C.An Efficient Approach for Reducing Harmonic Voltage Distortion in Distribution Systems with Active Power Line Conditioners［J］.IEEE Transactions on Power Delivery，2000，15(3):990-995.

［21］Booty W G，Lam D C L，Wong I W S，et al.Design and Implementation of an Environmental Decision Support System［J］.Environmental Modelling and Software，2000，16(5):453-458.

［22］Abbass H A. An Evolutionary Artificial Neural Networks Approach for Breast Cancer Diagnosis［J］.Artificial Intelligence in Medicine，2002，25(3):265-281.

［23］Niu Q，Zhou T J，Wang L.A Hybrid Particle Swarm Optimization for ParallelMachine TotalTardiness Scheduling ［J］. The International Journal of Advanced Manufacturing Technology，2010，49(5/6/7/8):723-739.