基于改进的角度偏差法的采空区点云数据精简

方源敏，夏永华，陈 杰，宋炜炜，杨永明，左小清

（昆明理工大学国土资源工程学院，云南昆明 650093）

0 引 言

地下采矿的采空区是一次整体爆破后形成的，是形状极不规则的复杂空间实体，出于安全考虑，人员不准许进入其内进行测量［1－3］。空区探测系统（CMS）可解决采空区的自动化测量，所获取的采空区三维激光点云数据虽然很精细，但是数据量大。如果设置成水平和垂直扫描间隔均为1°，扫描一个空区得到的三维坐标数据点接近50 000个，数据量超过2MB，一个中等矿山的采空区可能超过100个，仅空区数据量就会超过200MB。整个矿区三维地理信息系统的建立还需要很多其他空间数据，诸如矿体、井巷等，巨大的数据量将使存储、运算和传输效率低下，生成三维曲面模型的速度较慢，并且过于密集的点云会影响重构曲面的光顺性。因此，在采空区点云数据预处理中，必须在保证被测物体几何特征的前提下，根据物体的特征点对点云数据进行精简，提高曲面模型重构的效率。

很多学者对数据精简的研究已有一系列成果。Schroeder等提出了基于顶点删除的网格删减方法［4］；Turk给出了基于重新划分的模型简化方法［5］；Eck等将小波技术用于模型简化［6］；Filip等应用包围盒法来简化点云［7］；Lee等通过点云法矢量估算，运用八叉树数据结构，实现点云数据的空间精简［8］；刘德平等研究了自适应最小距离精简算法［9］；吴杭彬等总结激光扫描数据的特点，并基于其线扫描的特点，提出以扫描线斜率变化为准则实施数据压缩［10］；Yu等提出了一种自适应的三维点云数据精简算法［11］。这些方法只对某一种数据形式精简效果好，并且有些方法实现难度较大；因此，笔者提出了一种适合于采空区点云数据的精简算法——改进的角度偏差法。

1 点云数据精简算法评价体系

一个最佳的精简算法应该是利用最少的离散点就能达到全面表示空间复杂实体原有信息，并在此基础上追求更快的建模速度。点云数据精简算法的效果可以从以下3方面来衡量［11－13］。

（1）精度，即用精简后的点云数据构建的三维模型与原始三维模型之间的误差要小。数据精简后，不但要保证误差值在允许范围内，还要尽可能地保留原始点云特征。具体指标有长度、表面积、截面面积、体积、饱满度等。

（2）简度，即在保证精度的基础上尽量精简点云数据。需要指出的是，有时数据点数过少会给后续建模（例如三角网格化）带来困难，因此应根据实际需要选择合适的精简率。

（3）速度，即精简过程的时间耗费要尽可能少。即使满足精度和简度，但如果耗费时间太多，也难以在实际应用中推广。

实际上，要同时实现以上3个目标是不可能的，很多算法往往只能在一个或两个方面有优势。数据精简的最佳效果是使精简后的点云数据量较少、能保持细节特征且速度较快［14］。数据点在精简后的疏密应该随着曲面曲率的变化而变化，即曲率变化越大，数据点越多；曲率变化越小，数据点就越少。因此，在数据精简过程中，必须在保证被扫描实体几何特征的前提下，根据物体曲面的曲率变化对点云数据进行非均匀精简，以提高曲面重构的效率和精度。

2 CMS扫测采空区点云数据的方式

为了对点云数据进行精简，许多学者提出了很多点云数据精简算法。虽然点云数据精简算法很多，但是对于不同类型的点云数据需要采取不同的精简算法，才能达到理想效果［15－16］。

CMS是沿着事先设置好水平和竖直间隔角度形成线状扫描的系统［17］（图1）。根据CMS扫描获得的观测数据，笔者分析其本身的特点，并考虑扫描结构特征的影响，对数据进行精简处理，并用采空区扫描数据实例加以说明。在引入CMS之前，在安全条件允许的条件下，采用全站仪按一定间隔测量常规采空区断面，然后根据断面数据进行后续建模。假设密集的点云数据构成的点云包裹体是一个“真实”的采空区，在“真实”的采空区进行采样，可以采用某一条水平扫描线来进行分析，减少数据量的同时，还可将新的点集拟合成轮廓曲线，最后根据这些轮廓信息以及方向矢量信息重建曲面。

图1 空区探测系统扫测原理Fig.1 Scanning Principle of CMS

3 CMS扫描线特征点常规提取方法

CMS扫描线点云数据特征点的提取可以采用最小距离法、平均距离法、角度偏差法、弦高偏差法等［18－19］。以一条水平扫描线为例，分析这些方法对采空区扫描线点云数据进行精简处理的优缺点。

3.1 最小距离法

以扫描线为单位，事先设定一个最小距离dmin，然后沿扫描线方向，顺序比较相邻两点之间的距离d。若d＜dmin，则两点中的一个点将被删除，依次判断所有的扫描点。其中，最小距离应根据具体数据精简处理的精度要求来确定。这里取dmin＝0.5m，结果见图2。当采用最小距离法进行数据精简时，为了保证精度，只能采用较小的最小距离，这样数据的精简效率会明显减弱；为了保证效率，选用较大的最小距离，则不能更好地保持细节特征。

图2 最小距离法精简的扫描线结果Fig.2 Result of Scan Line Simplified by Minimum Distance Method

3.2 平均距离法

在每一条扫描线上，依次计算点与点之间的距离，平均距离为

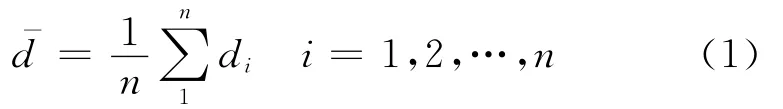
式中：d－为平均距离；di为点Pi与相邻点的距离；n为数据点个数。若di≤d－，则对应点Pi将被删除，反之则保留，精简结果见图3。这种方法原理很简单，但是无法保证扫描线的细节特征，不适合数据密集以及精度要求高的情况。

3.3 角度偏差法

引入角度αi来判断点Pi是否应该保留，事先设定一个角度阈值α（图4），如果αi≥α，则点Pi保留，否则删除，结果见图5。角度偏差法能够保持扫描线的细节特征，但在局部区域会出现点间距较大的情况。

3.4 弦高偏差法

图3 平均距离法精简的扫描线结果Fig.3 Result of Scan Line Simplified by Average Distance Method

图4 角度偏差法与弦高偏差法原理Fig.4 Principles of Angular Deviation Method and Chord Height Deviation Method

图5 角度偏差法精简的扫描线结果Fig.5 Result of Scan Line Simplified by Angular Deviation Method

对于n个数据点，通过计算每一个输入点和基线距离来判断某一测点是否应该删去（图4），精简结果见图6。弦高偏差法能够保持扫描线的细节特征，但在较平缓区域会出现点间距过大的现象。

4 CMS扫描线特征点的新提取方法

在对比最小距离法、平均距离法、角度偏差法、弦高偏差法等采空区点云数据精简方法的基础上，笔者提出了保留采空区几何特征更为有效的点云数据精简方法——改进的角度偏差法。

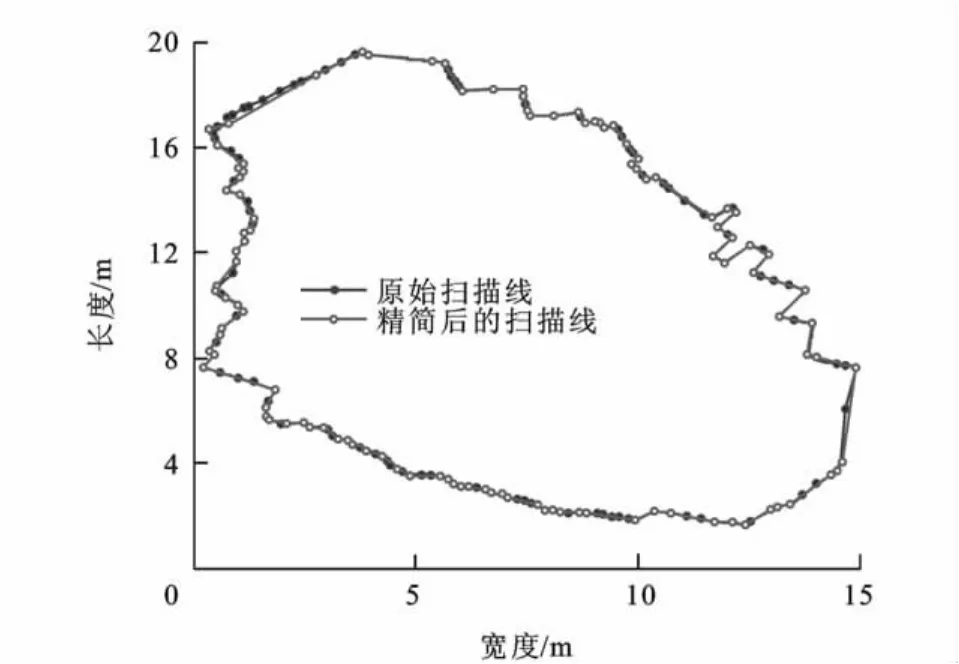
图6 弦高偏差法精简的扫描线结果Fig.6 Result of Scan Line Simplified by Chord Height Deviation Method

在图4中，Pi－1、Pi、Pi＋1为相邻3个点。αi为线段Li－1，i、Li，i＋1的夹角，a、b、c分别为点Pi与点Pi－1、点Pi与点Pi＋1以及点Pi－1与点Pi＋1的距离。它们存在如下关系

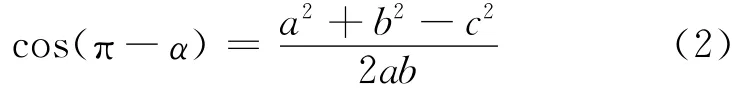
首先将一条扫描线（截面线）上的点云数据按顺序放到一个数组A中，根据式（2）顺序取3点Pi－1、Pi、Pi＋1，可求得点Pi的偏角。遍历这条截面线上所有点，即可求出该截面线上所有点的偏角，进而求出平均偏角值。将偏角值大于平均值的数据点提取出来，记录它在数组A中的编号，然后放到数组B中。这时，数组B中的数据点可能不是均匀分布的。改进的方法是：计算数组B相邻点的间距，将其与事先设定的阈值比较，如果间距大于阈值，以数组B中的这两点为端点，向数组B中插入两端点中点附近的数据点，所插入的数据点从数组A中提取，插入完毕后将数据存入数组C中，重复以上步骤，直到数组B中每两点之间的距离都小于阈值为止，这时，数组C中的点数据基本是均匀分布的。

图7显示了角度偏差法和改进的角度偏差法精简后的扫描线对比。显然，改进的角度偏差法精简后的数据不但保持了截面线的细节特征，还弥补了部分区域间距过大的问题，其各项指标见表1。

笔者提出的点云数据精简算法——改进的角度偏差法，原理简单，运算速度快，容易编程实现，虽然精简率相对于角度偏差法有所降低，但其他各项指标均优于角度偏差法。对每一条扫描线，利用上述算法进行处理，即完成了整个采空区的数据精简。

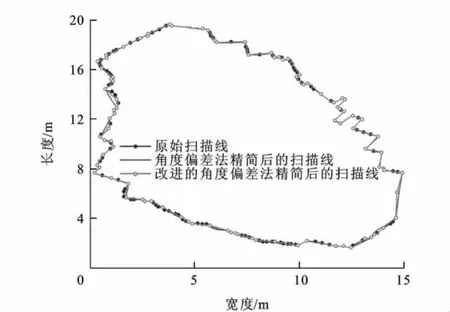
图7 角度偏差法与改进的角度偏差法精简的扫描线对比Fig.7 Comparison of Scan Lines Simplified by Angular Deviation Method and Improved Angular Deviation Method

表1 角度偏差法与改进的角度偏差法精简后的扫描线指标对比Tab.1 Comparison of Indicators of Scan Lines Simplified by Angular Deviation Method and Improved Angular Deviation Method

5 结 语

（1）CMS获取的采空区三维激光点云数据虽然很精细，但是数据量大，在运算和存储上都不方便，特别是在构建矿山三维地理信息系统时，大量采空区扫描数据会影响系统的运行速度。因此，有必要对采空区三维激光扫描点云数据进行有效精简。

（2）从CMS采集数据的特点入手，在分析了已有数据精简算法的基础上，提出了改进的角度偏差法，并运用该方法对采空区点云数据进行精简。

（3）改进的角度偏差法虽然耗时稍长，但精简效果理想，不但保持了扫描线上的细节，而且使精简后的点云数据较为均匀，为后续三维建模及应用打下良好基础。

References：

［1］ 来兴平.路基下大采空区动力灾害监测预报［J］.长安大学学报：自然科学版，2003，23（5）：28－31.LAI Xing－ping.Dynamical and Unstable Monitoring Signal of Large Scale Subsiding Area Under Roadbed［J］.Journal of Chang'an University：Natural Science Edition，2003，23（5）：28－31.

［2］ 计 宏，余学义，高志兴，等.彬长生产服务区下采空区稳定性评价研究［J］.西安科技大学学报，2011，31（5）：544－548.JI Hong，YU Xue－yi，GAO Zhi－xing，et al.Assessment on Stability of Mine Goaf in Binchang Production Service Area［J］.Journal of Xi'an University of Science and Technology，2011，31（5）：544－548.

［3］ 汤伏全，原 涛，汪桂生.渭北矿区厚黄土层采动变形数值模拟研究［J］.西安科技大学学报，2011，31（1）：53－58.TANG Fu－quan，YUAN Tao，WANG Gui－sheng.Mining Deformation Numerical Simulation of Thick Loess Layer in Weibei Mining Area［J］.Journal of Xi'an University of Science and Technology，2011，31（1）：53－58.

［4］ SCHROEDER W J，ZARGE J A，LORENSEN W E.Decimation of Triangle Meshes［J］.Computer Graphics，1992，26（2）：65－70.

［5］ TURK G.Re－tiling Polygonal Surfaces［J］.Computer Graphics，1992，26（2）：55－64.

［6］ ECK M，DEROSE T，DUCHAMP T，et al.Multiresolution Analysis of Arbitrary Meshes［J］.Computer Graphics，1995，29（2）：173－182.

［7］ FILIP D，MAGEDSON R，MARKOT R.Surface Algorithms Using Bounds on Derivatives［J］.Computer Aided Geometric Design，1986，3（4）：295－311.

［8］ LEE K H，WOO H，SUK T.Point Data Reduction Using 3DGrids［J］.The International Journal of Advanced Manufacturing Technology，2001，18（3）：201－210.

［9］ 刘德平，陈建军.逆向工程中数据精简技术的研究［J］.西安电子科技大学学报：自然科学版，2008，35（2）：334－339.LIU De－ping，CHEN Jian－jun.Point Data Reduction Technique in Reverse Engineering［J］.Journal of Xidian University：Natural Science Edition，2008，35（2）：334－339.

［10］ 吴杭彬，刘 春.三维激光扫描点云数据的空间压缩［J］.遥感信息，2006（2）：22－24.WU Hang－bin，LIU Chun.Spatial Compression of Point Cloud Data from Three Dimension Laser Scanning［J］.Remote Sensing Information，2006（2）：22－24.

［11］ YU Z W，WONG H S.ASM：an Adaptive Simplifica－tion Method for 3DPoint－based Models［J］.Computeraided Design，2010，42（7）：598－612.

［12］ 徐 尚.三维点云数据拼接与精简技术的研究［D］.青岛：中国海洋大学，2009.XU Shang.Study on Data Registration and Reduction for 3DPoint Clouds［D］.Qingdao：Ocean University of China，2009.

［13］ 温银放.数据点云预处理及特征角点检测算法研究［D］.哈尔滨：哈尔滨工程大学，2007.WEN Yin－fang.Research on the Algorithms of Point Cloud Pre－processing and Feature Corner Detection［D］.Harbin：Harbin Engineering University，2007.

［14］ WAND M，BERNER A，BOKELOH M，et al.Processing and Interactive Editing of Huge Point Clouds from 3DScanners［J］.Computers and Graphics，2008，32（2）：204－220.

［15］ 夏永华，方源敏，孙宏生，等.三维激光探测技术在采空区测量中的应用与实践［J］.金属矿山，2009（2）：112－113.XIA Yong－hua，FANG Yuan－min，SUN Hong－sheng，et al.Application Practice of 3DLaser Monitoring Technology in Finished Stope Survey［J］.Metal Mine，2009（2）：112－113.

［16］ 夏永华，方源敏，陈 杰，等.采空区点云数据的小波平滑方法［J］.湖南科技大学学报：自然科学版，2012，27（1）：84－87.XIA Yong－hua，FANG Yuan－min，CHEN Jie，et al.A Wavelet Smoothing Algorithm for Cloudy Data of Goaf［J］.Journal of Hunan University of Science and Technology：Natural Science Edition，2012，27（1）：84－87.

［17］ 赵 柳，马 礼，杨银刚，等.逆向工程中散乱点云数据精简研究［J］.光电技术应用，2010，25（1）：60－63.ZHAO Liu，MA Li，YANG Yin－gang，et al.Scattered Cloud Data Reduction Technique in Reverse Engineering［J］.Electro－optic Technology Application，2010，25（1）：60－63.

［18］ HUANG M C，TAI C C.The Pre－processing of Data Points for Curve Fitting in Reverse Engineering［J］.The International Journal of Advanced Manufacturing Technology，2000，16（9）：635－642.

［19］ 惠文华，郭新成.3D－GIS中空间曲线绘制方法研究［J］.地球科学与环境学报，2005，27（2）：63－65.HUI Wen－hua，GUO Xin－cheng.Method of Drawing Spatial Curves in 3D－GIS［J］.Journal of Earth Sciences and Environment，2005，27（2）：63－65.