动中找定 巧妙解题

●冯菊英 (金坛市第一中学 江苏常州 213200)

动中找定 巧妙解题

●冯菊英 (金坛市第一中学 江苏常州 213200)

动点问题、任意性问题能较好地考查学生的阅读、转化、化归、探索等能力，因此备受命题者的青睐．动点问题、任意性问题又与定点、定值、临界位置等相对不变量有关，因此在数学解题中应适时实现动与定的相互转化，充分挖掘题目中的隐含条件，巧妙解题．利用动定关系进行解题大体可分3类:(1)动中找定;(2)以静制动;(3)动静互化．本文对动中找定问题的常见类型进行归纳总结．

探索动点问题、任意性问题，常需研究曲线上的动点、函数中的变量等，解决的策略一般是:把握点运动的全过程，用运动与变化的眼光去观察研究，抓住其中的等量关系和变量关系．另外还应特别关注一些不变量、不变关系和特殊关系，抓住动态变化中暂时静止的某一瞬间，将其锁定在某一位置，化动为静，由特殊情形(特殊值、特殊点、特殊位置、特殊图形等)过渡到一般情形，问题的实质就容易显现出来，从而解决问题．

1 直接找到特殊位置

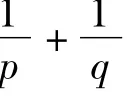
(3)极限法．将直线运动到与y轴重合的位置，此时弦的2个端点，一个在原点，一个在无穷远处，与的值一个是4a，一个是0，很快得出要求的结果．

注极端化策略在进行某些数学过程的分析时，具有独特作用，恰当应用极端原则能提高解题效率，使问题化难为易、化繁为简．极端化方法是特殊值法的延伸，着眼极端，把握过程，以静制动，用来解选择题、填空题往往思维深刻，过程简单明快，颇有举重若轻之感．

例2如图1所示，在正方体ABCD-A1B1C1D1中，点M是DD1的中点，点O是底面ABCD的中心，点P是棱A1B1上任一点，则直线OP与直线AM 所成角为 ＿＿．

分析因为点P是A1B1上任一点，所以OP是一条动直线，而要求的直线OP与直线AM所成角为定值，这实际上也是研究运动中不变量的问题．让直线OP运动起来，找到极端位置A1O，易知A1N是OP在面ADD1A1的射影，由正

方形的性质知A1N与AM垂直，再由三垂线定理得OP与直线AM所成角为90°．进一步，OP扫过的面A1B1O与AM垂直，从而得到更一般的结论．

对于此类在运动中探讨定值的问题，通常从运动中推测出事物将会达到的相对静止的局面，用静的方法来处理动的数量和形态，即直接找到特殊位置，再采用特殊法、极限法巧妙解决．由一般到特殊到极限是思维层次的提高，既省时又省力．

2 假定特殊位置、特殊值

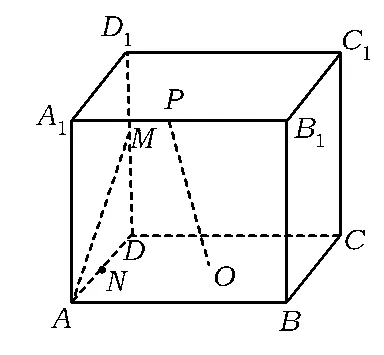
图1

例3如图2所示，已知2条直线 l1:2x－3y+2=0，l2:3x－2y+3=0，有一动圆(圆心和半径都在变动)与 l1，l2相交，且l1，l2被截在圆内的2条线段的长度分别是26和24，求圆心M的轨迹方程．

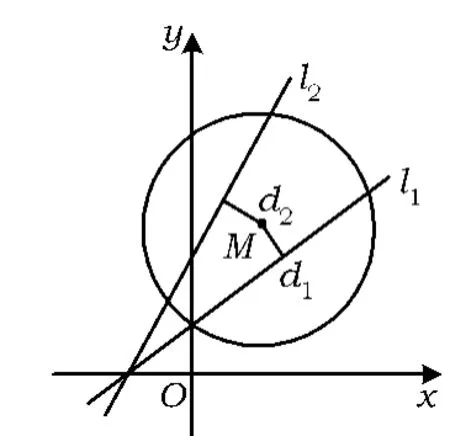
图2

分析该题中的圆是一个动圆，故可设定某个特殊位置，根据直线与圆的位置关系，再利用半径、半弦长、弦心距构成直角三角形，轻松解决问题!

注 求轨迹问题难在动点之“动”，如果能先让轨迹上的动点先“静止”(假定特殊位置)，继而寻找该点所满足的相关条件，用坐标列出其关系，再激活“静点”使其动起来，即得到所求的轨迹方程．注意学会从本质上认识问题，强化转化意识．

注假定变量为定值，是放缩法常采取的技巧．在用放缩法解题时，常因放缩过度而苦恼，采用极值放缩能达到放缩有度、顺应目标之效．

3 整合条件找定量

例5已知实数a，b，c成等差数列，点P(－1，0)在动直线ax+by+c=0上的射影为点M，点N的坐标为(2，1)，则线段 MN 长度的取值范围是＿．

分析由a，b，c成等差数列及ax+by+c=0为动直线可知，直线ax+by+c=0恒过定点，这样就将直线限制在绕定点旋转的区域内．在直线绕定点旋转的过程中结合射影这一条件再次寻找运动中的定量，从而解决问题．

解由a，b，c成等差数列知2b=a+c，代入直线方程得

在运动变化中探索问题，要善于在运动中抓住不变量，可以先取定特殊值或假定特殊位置，再考虑变量或点的运动，也可在点的运动过程中找到特殊位置或极限位置，还可整合条件找到条件中蕴藏的定量．由一般到特殊再到一般，是思维层次不断提升的过程，对培养学生数学思维能力、优化学生思维品质大有裨益．