表面等离子体环形共振器的滤波性质
2012-02-01陆文强
陈 靖,陆文强,孙 骞
(南开大学物理科学学院实验中心,天津300071)
1 引 言
近代物理实验是一门具有很强的综合性和技术性的实验课程,其内容涉及广泛:包含原子物理、核探测技术、激光、X射线、磁共振、微波技术、低温物理、半导体物理等.在课程的选题上,多数来源于在物理学发展史上起到了重大作用的经典实验.然而,随着近几十年来科技日新月异的发展,教师需要将与物理学密切相关的新内容、新技术、新方法及时充实到近代物理实验教学中,与时俱进,构成新的近代物理实验课程体系.因此,在经典的近代物理实验的基础上,我们需要将当代的研究成果转化为实验教学,增设新的研究型实验内容.
表面等离子体环形共振器滤波特性的研究就是研究型实验的代表之一.本文利用时域有限差分法(Finite-difference time-domain,FDTD)对基于金属-绝缘体-金属(Metal-insulator-metal,MIM)结构的表面等离子体环形共振器的滤波特性进行研究.分析了共振器各结构参量对其滤波性质的影响.本实验作为研究型实验是将目前的热门研究方向转化为实验教学内容,有利于本科生了解当今科学研究的前沿领域,学习逐步细化问题的科研方法,培养学生的创新能力、科研技能等综合实验素质.
2 基本原理
表面等离子体(Surface plasmons,SPs)是由外部电磁场(如光波)诱导金属表面自由电子集体振荡的一种特殊电磁模式.也就是说,表面等离子体是局域在金属表面的一种自由电子和光子相互作用形成的混合激发态[1-2].在这种相互作用下,自由电子在与其共振频率相同的光波照射下发生集体振荡.这种表面电荷振荡与光波电磁场之间的相互作用就构成了具有独特性质的SPs,光能被束缚在空间尺寸远远小于其自由空间波长的区域.在适当的金属-介质构成的光波导结构中,SPs不再受到衍射极限的限制,而可以被约束在纳米尺度内.基于SPs的这种特性设计高集成度的纳米光子器件,可以实现纳米尺度的光子集成.利用表面等离子体对光波在亚波长尺度上进行控制与操纵已经成为当今科研的热门领域,在纳米控光[3-4]、光传感[5]、超分辨率成像[6]、纳米光刻[7]等研究领域有着广泛的应用前景.基于SPs的MIM波导在理论和实验上已经被证明具有很强的亚波长光局域能力[8-9].因此,由MIM波导构成的金属共振器不但具有传统谐振器功能多样、波长选择性好等诸多优点,更以其尺寸小、结构紧凑等特点成为新一代纳米集成光路的基本元器件[10].
本文采用FDTD方法模拟了环形共振腔的滤波特性.FDTD是一个常用的模拟技术[11],其方法主要是将时间与空间网格化,在格点间距很小的极限情况下,将函数的微分运算转换成差分运算.在运用在麦克斯韦方程时,给定一初始场,模拟电磁波与材料的相互作用,与此电磁波随时间的演化行为.FDTD方法是直接对麦克斯韦方程组求解,并且除了在时间和空间上的数值离散处理以外,没有采用任何物理上的近似,这表明了FDTD方法在理论上是较精确的方法.现今,FDTD法作为基本的模拟方法已经被研究工作者广泛使用.
3 结构及模拟分析
本文中环形谐振器由2个MIM波导和1个环形波导组成,如图1所示.
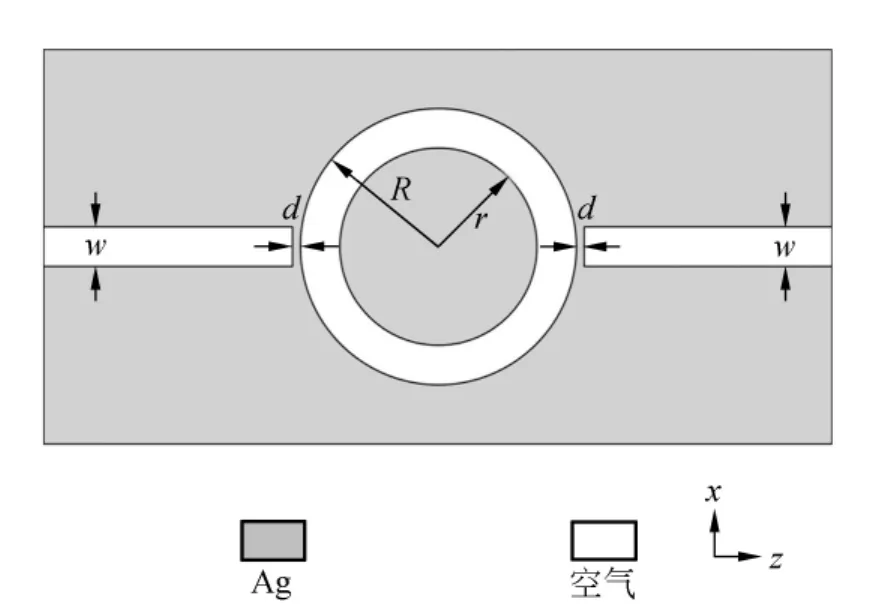
图1 环形谐振器结构示意图
2个MIM波导的宽度均为w=50nm;环形波导的外径为R=200nm,内径为r;MIM波导和环形波导的耦合距离为d.空气的折射率为n=1,Ag的电容率εm可以由Lorentz-Drude模型给出[12]:
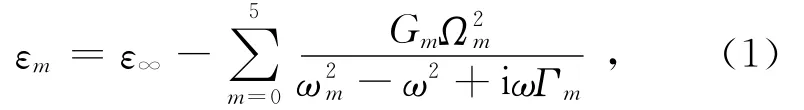
其中:ε∞为频率无限大时对应的相对电容率,Gm为振子强度,Ωm为等离子体频率,ωm为谐振腔共振频率,Γm为阻尼因数,ω为入射光角频率.上述所有参量的选取均来源于文献[12].环形共振腔中的共振波长可以写为
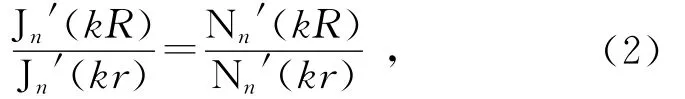
其中:k为环形腔中的波矢,Jn为n阶第一类Bessel函数,Nn为n阶第二类Bessel函数.由式(2)可以得知,Bessel函数的不同阶数n对应了不同波长的共振模式,并且共振波长受环形波导半径调制.
3.1 利用FDTD方法模拟MIM环形波导的滤波特性
根据计算经验,FDTD模拟计算中使用的元胞大小dx=dz=2nm.这样的元胞不但可以达到所需的计算精度,同时在数值模拟所需要的时间也是可以接受的.
入射光从MIM波导左端沿z轴方向以TM模式入射,入射光电场量的振幅为1V/m,其半高全宽为(FWHM)与MIM波导的宽度相等.图2为r=150nm,d=10nm时环形共振腔的透射情况.只有满足式(2)的入射光才能被有效地传输,其他波长被损耗截止.由图2环形共振器的透射谱可以看出共存在3个共振模式,对应的共振波长分别为1 618nm,822nm和568nm.它们的场强分布如图3(a)~(c)所示.在模式Ⅰ下,环形波导中存在2个波节;在模式Ⅱ下,环形波导中存在4个波节;在模式Ⅲ下,环形波导中存在6个波节.
根据式(2)可知,共振波长受环形波导半径调制.本文研究环形波导内径r对共振器透射光谱的调制.选取MIM波导宽度w=50nm,耦合距离d=10nm,透射谱随环形波导内径r的变化曲线如图4所示.随着波导内径r的增加,共振波长将发生红移.透射率随内径的增大而减小,这是由于随着波导内径的增大,光在MIM共振腔中的传播长度增加,欧姆损耗也会随之增强,因此透射光强将会降低.
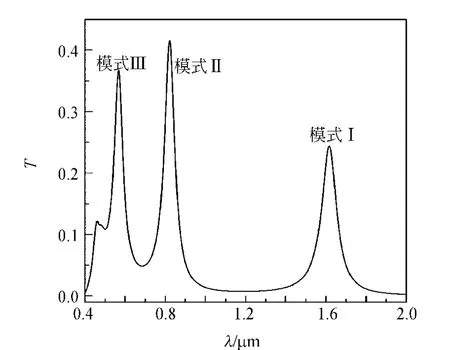
图2 环形共振腔的透射谱
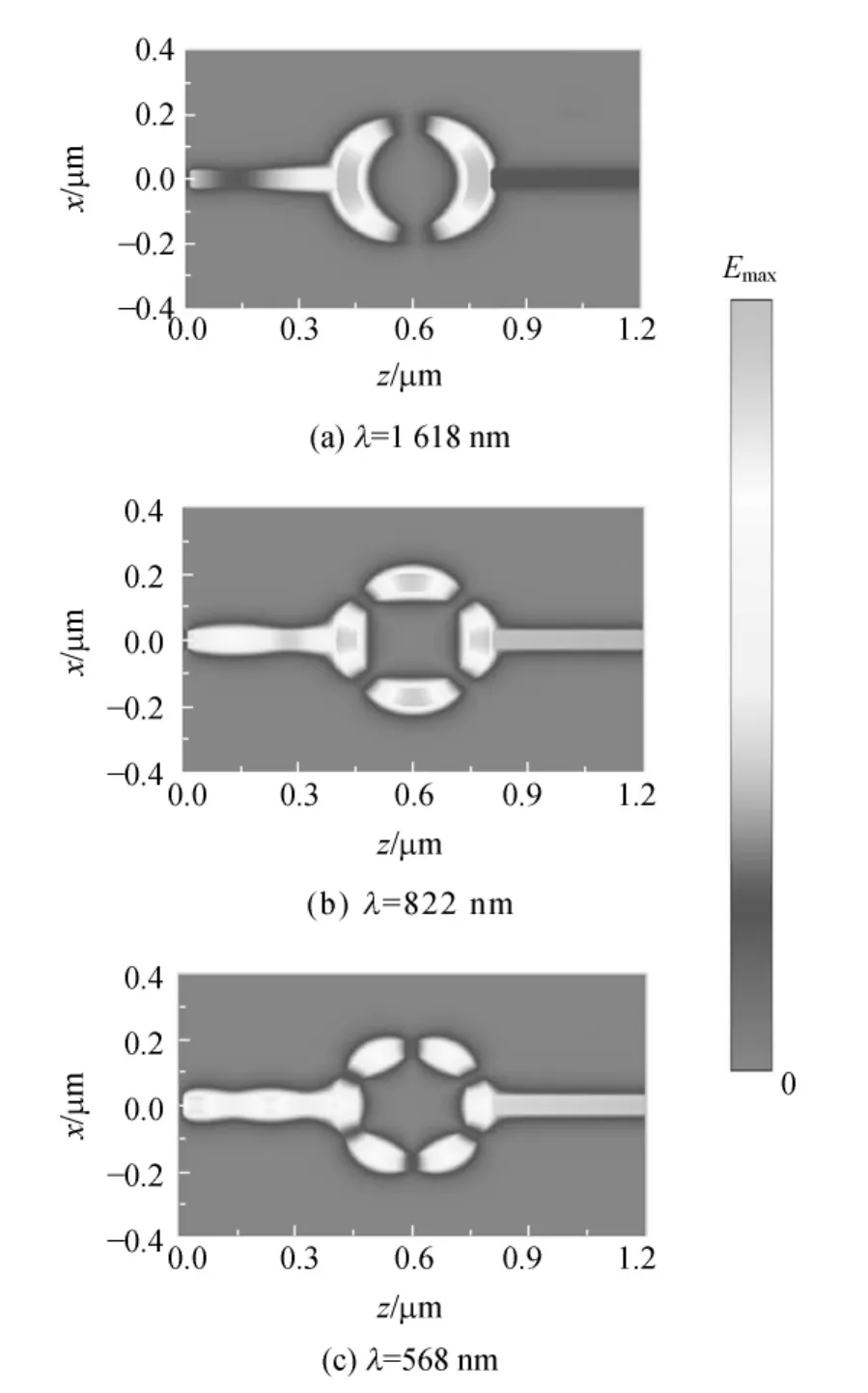
图3 磁场Hy分布图
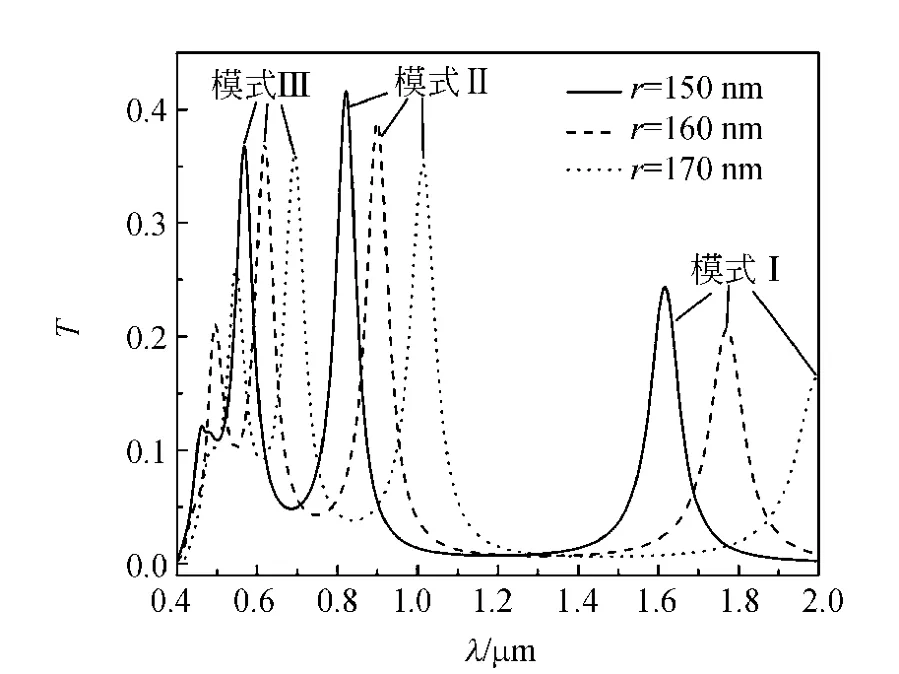
图4 共振腔透射谱线随环形波导内径r变化曲线
3.2 MIM共振腔的耦合距离d对透射谱的影响
选取环形波导内径r=150nm,MIM波导宽度w=50nm,模拟结果如图5所示.模拟结果表明,随着耦合距离d的增加,共振波长有微小的蓝移,透射率也随之下降.但是随着d的增加,3个模式下的共振峰带宽都显著地减小,当耦合距离d=20nm时,模式Ⅱ和模式Ⅲ的带宽分别降至24nm和21nm.共振峰带宽随耦合距离d的变化曲线如图6所示.
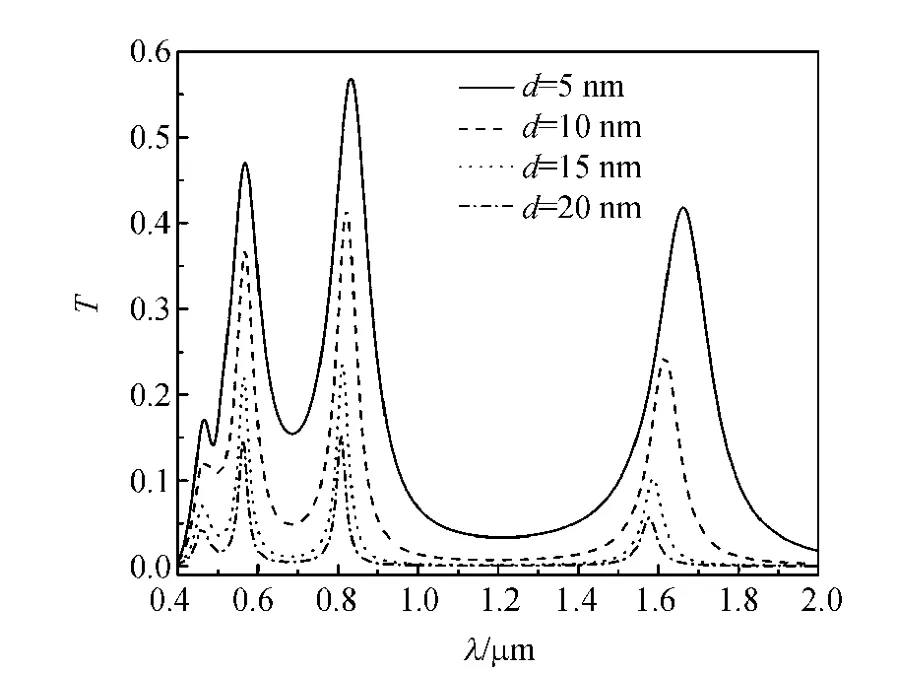
图5 共振腔透射谱随耦合距离d变化曲线
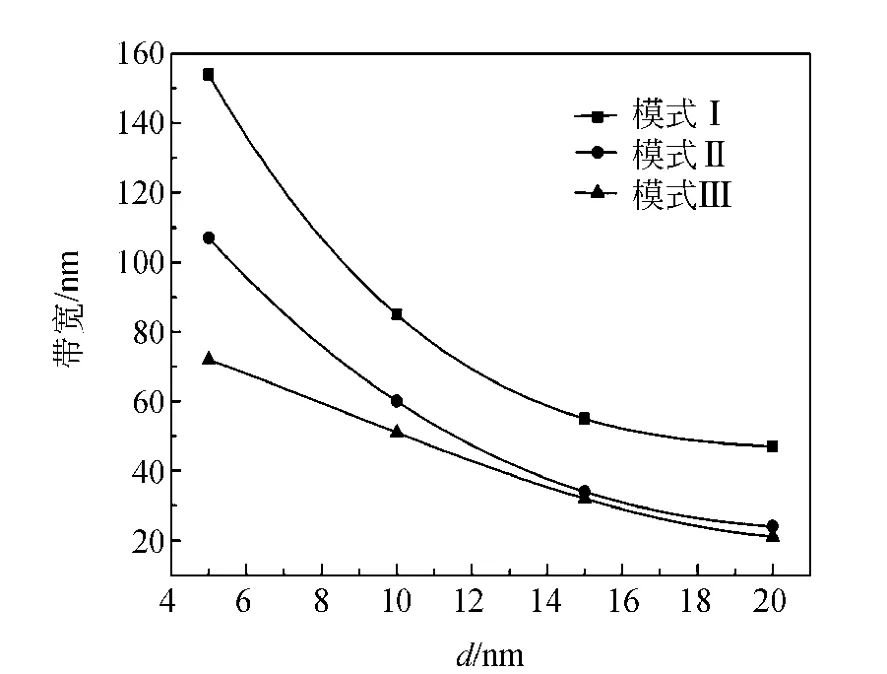
图6 耦合距离d与共振峰带宽的关系
3.3 MIM波导宽度w对共振腔滤波特性的影响
选取环形波导内径r=150nm,耦合距离d=10nm,透射谱随w的变化曲线如图7所示.
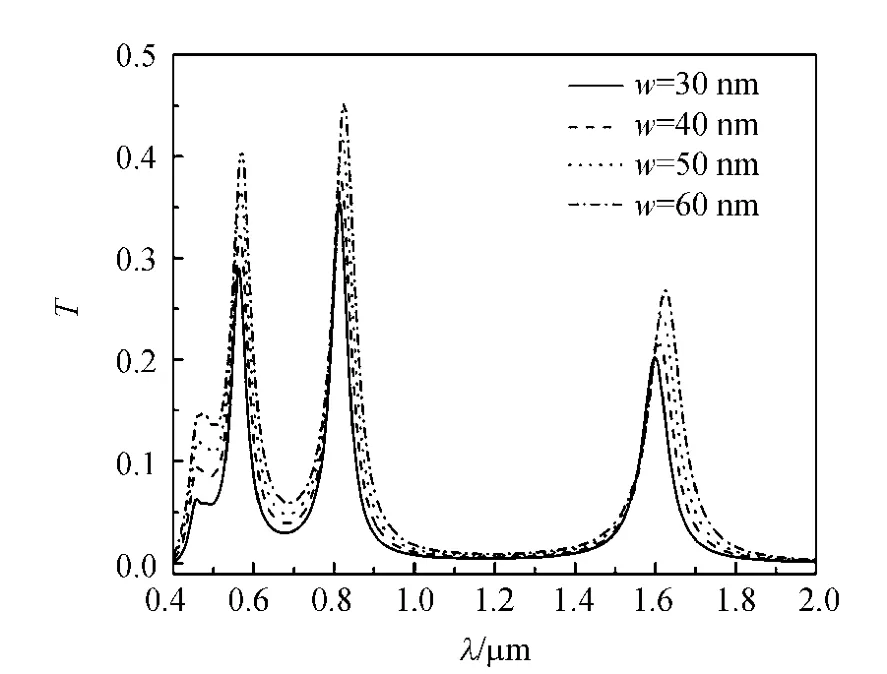
图7 共振腔透射谱随MIM波导宽度w变化曲线
结果表明,随着MIM波导宽度w的增加,共振峰会发生微小的红移,透射率也有微小的增强.根据所得结果,可以认为波导宽度对环形共振腔透射谱的影响极小.
4 结束语
基于MIM结构的环形共振器的滤波特性显示了其在纳米光子集成中应用的巨大潜力.学生通过本实验的学习,了解当今科研的前沿领域,理解基于SPs的MIM环形共振器的基本原理.通过对结构各个参量的细化分析研究,使学生学习科研的基本思维方式,掌握分析实验数据和推断实验结果的方法,培养学生的创新能力、科研技能等综合实验素质[13].
[1] Barnes W L,Dereux A,Ebbesen T W.Surface plasmon subwavelength optics[J].Nature,2003,424(6950):824-830.
[2] Lezec H J,Degiron A,Devaux E,et al.Beaming light from a subwavelength aperture[J].Science,2002,297(5582):820-822.
[3] Veronis G,Fan S.Bends and splitters in metal-dielectric-metal subwavelength plasmonic waveguides[J].Appl.Phys.Lett.,2005,87(13):131102-1-3.
[4] Gramotnev D K,Nielsen M G,Tan S J,et al.Gap surface plasmon waveguides with enhanced integration and functionality[J].Nano.Lett.,2012,12(1):359-363.
[5] Liu Q,Chiang K S.Refractive-index sensor based on long-range surface plasmon mode excitation with longperiod waveguide grating[J].Opt.Express,2009,17(10):7933-7942.
[6] Fang N,Lee H,Sun C,et al.Sub-diffraction-limited optical imaging with a silver superlens[J].Science,2005,308(5721):534-537.
[7] Luo X G,Ishihara T.Surface plasmon resonant interference nanolithography technique[J].Appl.Phys.Lett.,2004,84(23):4780-4782.
[8] Shin H,Yanik M E,Fan S,et a1.Omnidirectional resonance in a metal-dielectric-metal geometry[J].Appl.Phys.Lett.,2004,84(22):4421-4423.
[9] Abad J B,Moreno L M,Vidal F J G.Transmission properties of a single metallic silt:From the subwavelength regime to the geometric-optics limit[J].Phys.Rev.E,2004,69(2):026601-1-6.
[10] Wang T B,Wen X W,Yin C D,et al.The transmission characteristics of surface plasmon polaritons in ring resonator[J].Opt.Express,2009,17(26):24096-24101.
[11] Yee K.Numerical solution of initial boundary value problems involving maxwell’s equations in isotropic media[J].IEEE Transactions on,1966,14(3):302-307.
[12] Rakic A D,Djurisic A B,Elazar J M,et al.Optical properties of metallic films for vertica-cavitiy optoelectric devices[J].Appl.Opt.,1998,37(22):5271-5283.
[13] 陈靖,陆文强,孙骞.利用时域有限差分法模拟介质纳米波导的波导特性[J].物理实验,2010,30(9):7-10.
