利用井下孤点进行测量的方法

2012-02-01王银锋李赟瑜

科技传播 2012年1期

王银锋,李赟瑜

陕西陕煤韩城矿业有限公司,陕西西安 710014

0 引言

所谓孤点，顾名思义就是点是孤立的，它们之间没有任何联系。在煤矿由于开采等原因使得敷设在巷道内的一些导线点遭到破坏，其残存的导线点可能成为孤点，它们互不通视，无法直接使用。现要在某个孤点附近施工需要进行测量放线工作，如果从距离该孤点较远的永久导线点重新测量，不仅占用巷道时间较长影响矿井生产，而且由于测站过多给本来测量人员就少的地测部门带来很多困难，加之距离长测量精度亦无法保证。那么怎样才能做到既不影响生产又使测量工作量最小，就成为我们测量人员急需解决的问题。笔者认为，完全可以利用该孤点和其它孤点来进行测量。

1 施测方法

首先在孤点之间布设支导线，进行常规导线测量，再根据测量结果，进行施工所需的测量或引测放线工作。

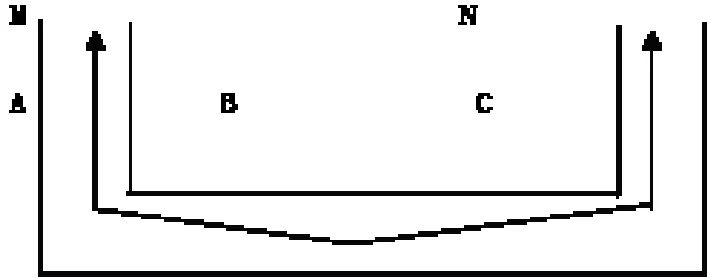
下面以两个孤点为例，来说明其施测方法。如下图所示，在某矿井下有孤点M（XM,YM）.N（XN,YN）,在MN之间敷设支导线，A、B、C为新设支导线点。

施测时，严格按照《煤矿测量规程》关于井下控制测量的技术要求及经纬仪导线测量的外业观测程序进行。测得∠A、∠B、∠C及边SMA、SAB、SBC、SCN（为了叙述方便，假设这些边长已经换算为水平长），并保证观测结果在允许限差范围内。

2 导线计算

2.1 三角形计算

连接MB、MC、MN,分别构成△MAB、△MBC、△MCN。

在△MAB中，SMA、SAB、∠A已知，由余弦定理可以求得：

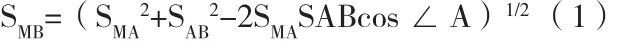
根据式（1）求出SMB，结合SMA、SAB、∠MAB,由正弦定理可得出：

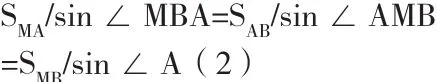
从而求得：

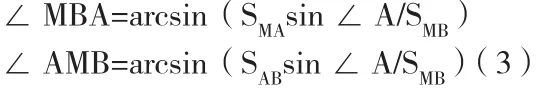
在△MBC中，根据导线实测资料及式（3）的计算结果可以求得：

结合式（1），同样的办法可以求得SMC以及∠MCB、∠BMC。

按照上面的办法，同样可以在△MCN中，求出SMN、∠CMN和∠MNC，这里就不在赘述了。

2.2 导线计算

2.2.1 方位角计算

首先我们根据两个孤点的已知坐标进行反算，可求出MN的边长和方位角，即

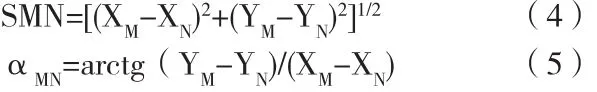
然后根据3.1中所求得的这些角度，可以很容易地推导出第一条导线边的方位角。再由第一条边的方位角和所测导线的夹角可以推算出其它各边的方位角。下面我们以M点位起始点，推导如下：

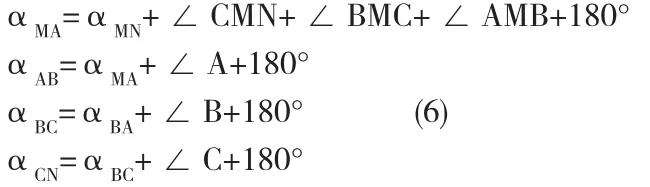
2.2.2 坐标计算

由于各导线边的方位角已经求出，边长已经测出，所以各个导线的坐标就可以计算出来。

3 检核

3.1 角度检核

由于工作环境、仪器本身、测量人员等因素影响，测量工作不可避免的存在误差，以及计算过程中的凑整，可能使得△MAB、△MBC、△MCN的内角和不等于180°，多边形MABCN的内角不等于（n-2）180°，其差值符合要求时，说明导线测量和三角形计算结果是正确的，可按规定予以分配。若差值超过规定，应检查导线测量的外业资料及计算资料，必要时应重测。

3.2 边长检核

根据MN的边长进行检核，具体方法是：比较由M、N点坐标反算的MN边的长度和由解算△所得到的MN边的长度。如果其长度的差值符合要求，说明测量过程和计算结果均正确，否则说明测量过程和计算结果有问题，必须对其重测重算。

3.3 坐标检核

我们从M点的坐标推算出N点的坐标应该与已知值相等，但由于测量误差和计算凑整，可能使N点的坐标推算值与已知值不符，即存在闭合差。当相对闭合差满足《煤矿测量规程》的精度要求时，可以认为导线测量的外业和内业计算结果是正确的。其闭合差应与坐标增量成正比进行分配。如果相对闭合差超限，首先要检查外业资料和内业计算资料，确认没有问题时，必须重测。

另外，将所计算的ABC等点的坐标及时上平面图，也可以起到检核的作用。如果这些点不在图上巷道内而跑到了巷道的外面，一般情况下孤点用错所致。同时可以根据这些点在巷道的位置以及到巷道特征点的距离等进行检核。