城市表层土壤重金属污染分析

李彩霞，何胜男，田雷霞

河南省新乡市河南师范大学，河南新乡 453007

1 问题重述

随着城市经济的快速发展和城市人口的不断增加,人类活动对城市环境质量的影响日显突出.对城市土壤地质环境异常的查证,以及如何应用查证获得的海量数据资料开展城市环境质量评价,研究人类活动影响下城市地质环境的演变模式,日益成为人们关注的焦点。

按照功能划分,城区一般可分为生活区、工业区、山区、主干道路区及公园绿地区等,分别记为1类区、2类区、……、5类区,不同的区域环境受人类活动影响的程度不同。

现对某城市城区土壤地质环境进行调查.为此,将所考察的城区划分为间距1km左右的网格子区域,按照每平方公里1个采样点对表层土（0cm～10cm深度）进行取样、编号,并用GPS记录采样点的位置.应用专门仪器测试分析,获得了每个样本所含的多种化学元素的浓度数据.另一方面,按照2km的间距在那些远离人群及工业活动的自然区取样,将其作为该城区表层土壤中元素的背景值。

附件1列出了采样点的位置、海拔高度及其所属功能区等信息,附件2列出了8种主要重金属元素在采样点处的浓度,附件3列出了8种主要重金属元素的背景值。

现要求你们通过数学建模来完成以下任务：

1）分析该城区内不同区域重金属的污染程度；

2）通过数据分析,说明重金属污染的主要原因；

3）分析重金属污染物的传播特征,由此建立模型,确定污染源的位置。

2 模型假设

1）假设各元素浓度的测量准确无误；

2）假设重金属元素是从高浓度到低浓度扩散；

3）假设重金属元素向3个方向上的扩散系数相同,且不受降雨等外部因素影响。

3 模型的建立和求解

3.1 问题一：模糊数学模型[1]

传统评价方法仅仅考虑了重金属污染物浓度超标的情况,未考虑重金属本身的毒性作用,这就有可能掩盖有些浓度低但毒性大的有毒物的污染作用,因此,采用基于双权重因子的模糊数学模型综合考虑重金属浓度和毒性作用进行评价更为全面合理.根据模糊评价的原理、步骤及查得的土壤重金属污染程度分级标准及生物毒性指数（如表1）进行求解。

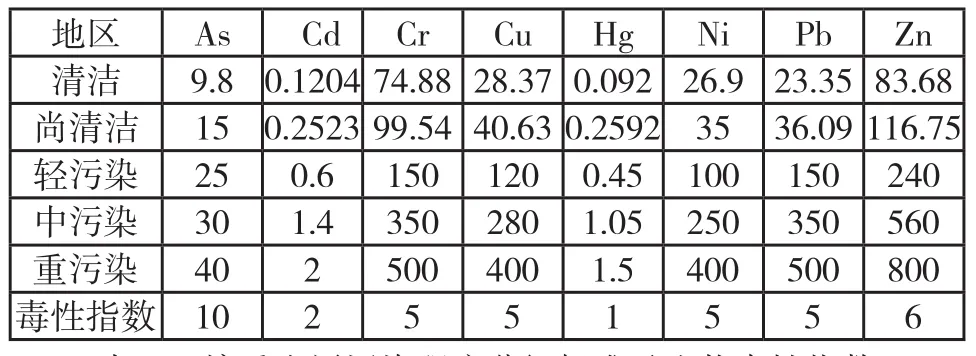
表1 土壤重金属污染程度分级标准及生物毒性指数

模型的求解过程具体如下：根据附表一实测数据各区各重金属元素求得的平均值和表2的数据,计算各重金属元素对应于各土壤重金属环境质量等级的隶属度函数,得到关系模糊矩阵。如功能区一经计算后得到的关系模糊矩阵为：

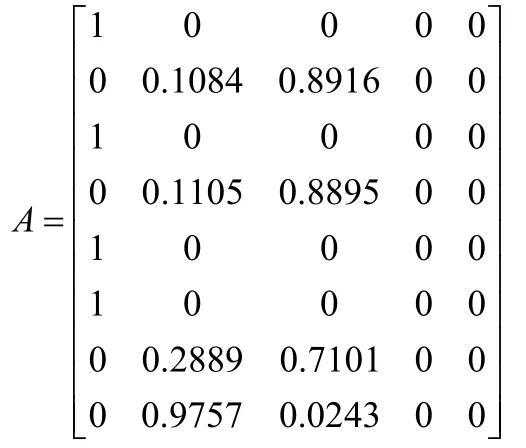
由附表1实测数据和表2数据得到功能区一各个重金属参评因子的权重

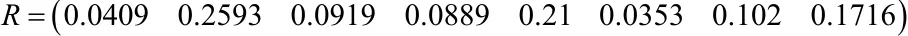
根据功能区一的模糊关系矩阵和对应的权重系数可得出功能区一对评价等级的隶属度,再根据最大隶属度原则,确定各样品的污染程度,此即为土壤环境质量分级。

其他四区的具体做法和功能区一样,在这里不再赘述,结果见下表。

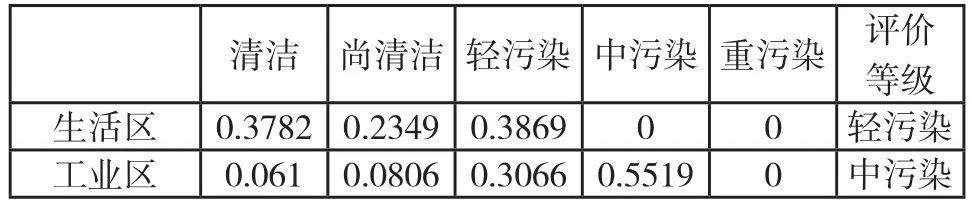
表2 模糊综合评价结果

山区 0.6664 0.2201 0.1135 0 0 清洁主干道路区 0.0781 0.6324 0.1979 0.0916 0 尚清洁公园绿地区 0.1842 0.3912 0.4246 0 0 轻污染

3.2 问题二：主成分分析数学模型

八种重金属元素在五个功能区的分布不同,对区内重金属污染的影响也不同,故该模型采用主成分分析法建立,通过SPSS软件分别得到五个功能区的主成分值，进而得到各功能区污染的主要因素.

3.2.1 主成分值

表3 城区主成分值

1）主成分一中各因子的载荷值比较大的是Cu、Pb分别为75.6%、76.4%；

2）主成分二中各因子的载荷值都较小。

因为工业生产原料和工业污染里含有大量Cu、Pb元素,因此可认为对整个城区而言重金属污染的主要原因是工业废物。

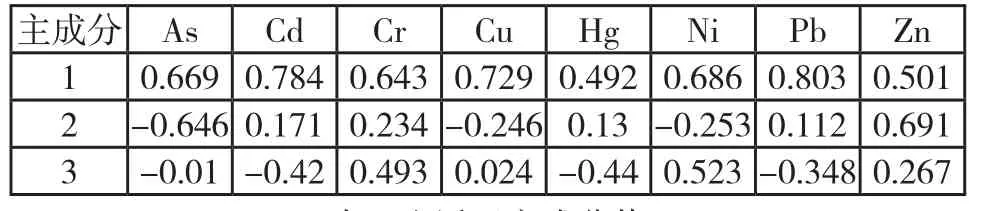
表4 生活区主成分值

1）主成分一中各因子的载荷值比较大的是Cd、Cu、Pb分别为78.4%、72.9%、80.3%；

2）主成分二和三中各因子的载荷值都较小。

因子变量在Cd、Cu、Pb上有较高的载荷,是因为城市垃圾中含有的Cd、Cu、Pb、Zn平均含量分别为9、350、330和780（mg/kg）,主成分因子在Zn上的载荷不高,可能是因为Zn的毒性系数较低的缘故,另外Cu、Pb还可能来自于工业污染,Pb可能来自于尾气排放。

表5 工业区主成分值

1）主成分一中各因子的载荷值比较大的是Cr、Cu、Pb、Zn分别为91.6%、86.8%、85.8%、85.9%；

2）主成分二中各因子的载荷值都较小。

因子变量在Cr、Cu、Pb、Zn上有较高的载荷,表明主要受工业污染排放的影响.

表6 主干道路区主成分值

1）主成分一中各因子的载荷值比较大的是Cr、Cu、Ni分别为87.4%、90.6%、88.8%；

2）主成分二中各因子的载荷值都较小。

因子变量在Cr、Cu、Ni上有较高的载荷。Ni来自于汽车车体的磨损、车胎的老化以及冶金工业等,反映了交通污染本身产生的影响。Cr、Cu载荷较高说明该地区受到工业污染的影响。

表7 公园区主成分值

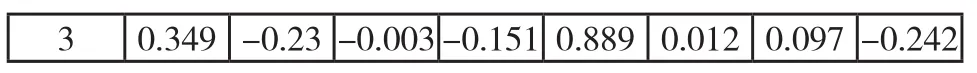
3 0.349-0.23-0.003-0.151 0.889 0.012 0.097-0.242

1）主成分一中各因子的载荷值比较大的是Cd、Cr、Pb、Zn分别为81.1%、80.9%、78.2%、79.2%；

2）主成分二中各因子的载荷值都较小；

3）主成分三中Hg的载荷值比较大为88.9%。

公园不可能产生重金属污染,考虑到公园一般位于市中心,所以不可避免的受到生活污染、工业污染、交通污染的影响,Cd、Pb、Zn可能来自生活垃圾,Cr来自工业污染,Pb来源比较广泛。

3.3 问题三：基于扩散过程和质量守恒的微分模型[2]

由前两问的数据分析了解到交通区Cr、Cu有较高的载荷,说明该地区受到工业污染的影响较大,而公园区则受到生活污染、工业污染、交通污染等多方面的影响.据此,说明重金属是由浓度高的地区扩散到浓度低的地区,传播的媒介是大气和水,此外重金属一个很重要的特征是难降解,即在传播中保持质量守恒.重金属的传播过程可近似于物理中的扩散过程,基于此建立微积分模型。

以u( x, y, z)表示空间某点( x, y, z)在t时刻污染物的浓度,任取空间一闭曲面S,其所围区域为Ω。由于扩散,通过S,t到t+∆t时间内扩散入的重金属质量为

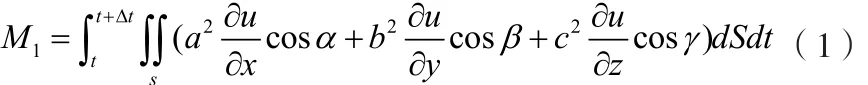
其中,,α β γ分别为曲面S上(,,) x y z处外法向量的方向角.

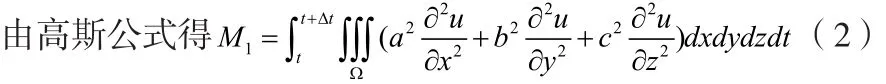
其中 a2, b2, c2为三个方向上的扩散系数。由于吸收衰减,在t到t +∆t时间内,Ω 内重金属的减少为

其中k为吸收衰减系数.

设Q(,,) x y z为(,,) x y z点上t时刻单位体积单位时间内的重金属排放量,S内t到t t+∆时间内共排放的重金属量为

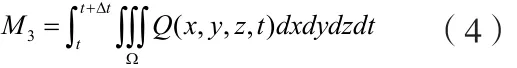
同时,由于浓度变化引起S内重金属质量增加量为

当k=0与Ω＞0同时成立时,该点位污染源,否则该点不是污染源.

经MATLAB求解和具体分析[3],结合上题,剔除点22,最终确定的污染源在样本点9,182,8,257,41,232,93,29,145,49点处或附近。

[1]窦磊，周永刚，王旭，等.针对土壤重金属污染评价的模糊数学模型的改进与应用.土壤通报，2007,38(1)：101-104.

[2]蔡锁章.数学建模原理与方法.北京：海洋出版社，2000.

[3]汪哓银，邹庭荣.数学软件与数学实验.北京：科学出版社，2008.