试用Excel函数实现检测数据的修约
2012-01-29寸松梅杨一云杨国先杨军慧
寸松梅,杨一云,杨国先,杨军慧
(云南省烟草公司保山市公司,云南 保山 678000)
在检测工作中,检测结果是符合精密度要求的两次测定结果的平均值,并按照数据修约规则进行修约后报出。而Excel提供的ROUND函数遵循的是四舍五入的原则,修约规则遵循的是四舍六入五考虑的原则,即用Excel现成的函数无法实现检测数据的修约,一般情况下只能采取人工修约。当检测样品数量在20个以上,要对每个样品的各检测项目的检测平均值进行人工修约时,每个数据都要使用一遍修约规则,一是费时,二是容易疏漏,三是疏漏后不容易检查,给检测人员带来了很大的麻烦。为了解决这一问题,笔者应用 Excel中的 IF、AND、INT、EVEN、FIXED、ROUND函数编写命令,使Excel应用软件在数据处理时能按数据修约规则进行修约。
1 修约规定及检测数据的报出要求
当拟舍弃数据的最左一位数字为5,且其后无数字或皆为0时,若所保留的末位数字为奇数(1,3,5,7,9)则进一;若所保留的末位数字为偶数 (0,2,4,6,8),则舍去[1]。检测数据的报出以两次测定的平均值作为测定结果,测得的项目含量≥10.0%,结果精确至 0.1%[2]; <10.0%,结果精确至 0.01%[2~6]。
2 数据的分解
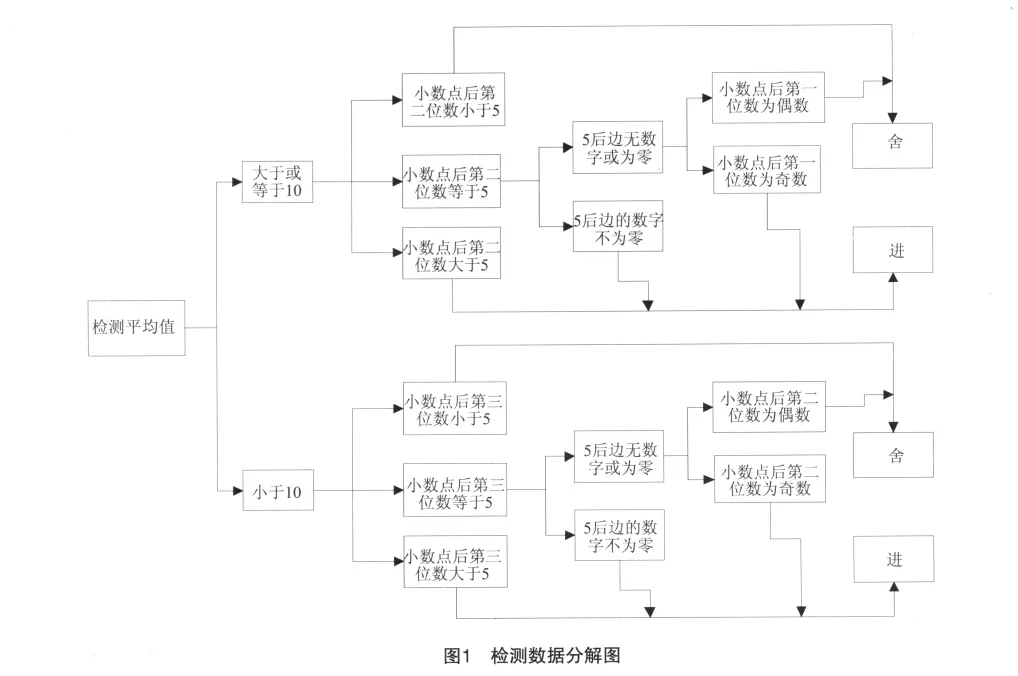
按检测数据的报出要求,将检测数据分解为≥10.0%与<10.0%两部分,然后又分别对每一部分进行分解。
如图1所示,这两部分数据的分解是相同的,所不同之处仅在于小数位数的不同,≥10%的考虑的是小数点后第二位数的进舍,<10%的考虑的是小数点后第三位数的进舍。
按欲舍弃数字的最左一位<5、=5、>5将检测数据分成三个部分,其中欲舍弃数字的最左一位<5、>5的这两部分数据按四舍五入原则进行修约;欲舍弃数字的最左一位=5的这一部分数据,又分成5右边的数字为零或不为零两部分,其中5右边的数字不为零的数据按四舍五入原则进行修约,5右边无数字或为零的又可分成保留的末位数为偶数或奇数两个部分,其中保留的末位数为奇数时5就要进,保留末位数为偶数时5就要舍。
3 数据的处理及命令的编写
3.1 数据的筛选处理
按照数据分解的思路,先考虑≥10这一部分,将数据分成10~20、20~30、30~40等几个段,这几个段的数据都是小数点后两位数从00逐渐逼近99,我们主要看每一段中小数点后第二位数是5并且5后边没有数字的数据,也就是说发生进或舍的是小数点后第二位的数字,小数点前面的数字不存在进舍也就不存在变化,因此我们只要找出其中一段的处理方法,就可以解决其他段。推而广之,<10的检测数据同样可以这样分段,只不过考虑的是小数点后第三位的数字。
以10.00~10.99的数据为例来进行筛选。如表1所示,先将小数点后第二位数是5,并且它后边的数全部为零或没有数字的这一类数据筛选出来。因为保留位数为小数点后一位,考虑的是小数点后两位的数字。
通过观察,当数据扩大10倍并且再乘以2时,只有小数点后一位数是0或5并且0或5后边无数字或数字全为零的结果是整数,其它的数据 (包括小数点后第二位是5但其后边有数字的)乘以2以后的结果均不成整数,因此对结果进行取整,看取整与不取整的结果是否相等,将小数点后第二位数是0或5并且0或5后边没有数字的数据筛选出来,即 10.00、10.05、10.10、10.15、10.20、10.25、10.30、10.35、10.40、10.45、10.50、10.55、10.60、10.65、10.70、10.75、10.80、10.85、10.90、10.95。再观察筛选出来的数据,发现小数点后第二位是5的数乘以10的结果不是整数,而小数点后第二位数是0的数乘以10以后是整数,因此对结果进行取整,令检测结果乘以10取整后的结果小于检测结果乘以10,就将小数点后第二位是5并且5后边无数字或全为零的数据筛选出来,即10.05、10.15、 10.25、 10.35、 10.45、 10.55、 10.65、10.75、10.85、10.95。
3.2 数据的分析处理
3.2.1 ≥10的处理
数据筛选完成后,考虑的就是筛选出来的数据的处理。按照规则要求,小数点后一位是奇数的使5向前进一,小数点后一位是偶数的将5舍去。
再如表1所示,来看筛选出来的数据乘以10以后的结果,即 100.5、101.5、102.5、103.5、104.5、105.5、106.5、107.5、108.5、109.5,数据乘以10以后就全部变成小数点后一位数为5。将结果取整,这时小数点后第二位的5就全部被舍去,变成整数100~109。若再将结果向上取偶数,由于取的是向上最接近的偶数,因此取整后的结果是:偶数的仍然不变 (如100取整为100、102取整为102、104取整为104、106取整为106、108取整为108),取整是奇数的则被向上进一成为偶数 (如101取整为102、103取整为104、105取整为106、107取整为108、109取整为110),这时将取整结果再除以10,将检测数据还原为10.0、10.2、10.4、10.6、10.8、11.0,实现了小数点后第一位是偶数的其小数点后第二位的5被舍去,而小数点后第一位是奇数的其小数点后第二位的5被向前进一。
除筛选出来以外的数据,按四舍五入原则进行修约,保留一位小数。
为了使数据中的整数返回结果为小数点后两位,将结果全部按规定的位数取整。
3.2.2 <10的数据的处理
<10的数据的筛选和处理方法与≥10的相同,不同之处在于因数据保留小数点后两位小数,因此将条件中的乘以20改为乘以200,乘以10改为乘以100后,同样实现小数点后第三位数为5并且5后边无数字或全为零,小数点后第二位是偶数时5
被舍去,小数点后第二位是奇数时5向前进一,其他数据执行四舍五入原则,保留小数点后两位。为了使数据中的整数返回结果为小数点后为两位数,将结果全部按规定的位数取整。
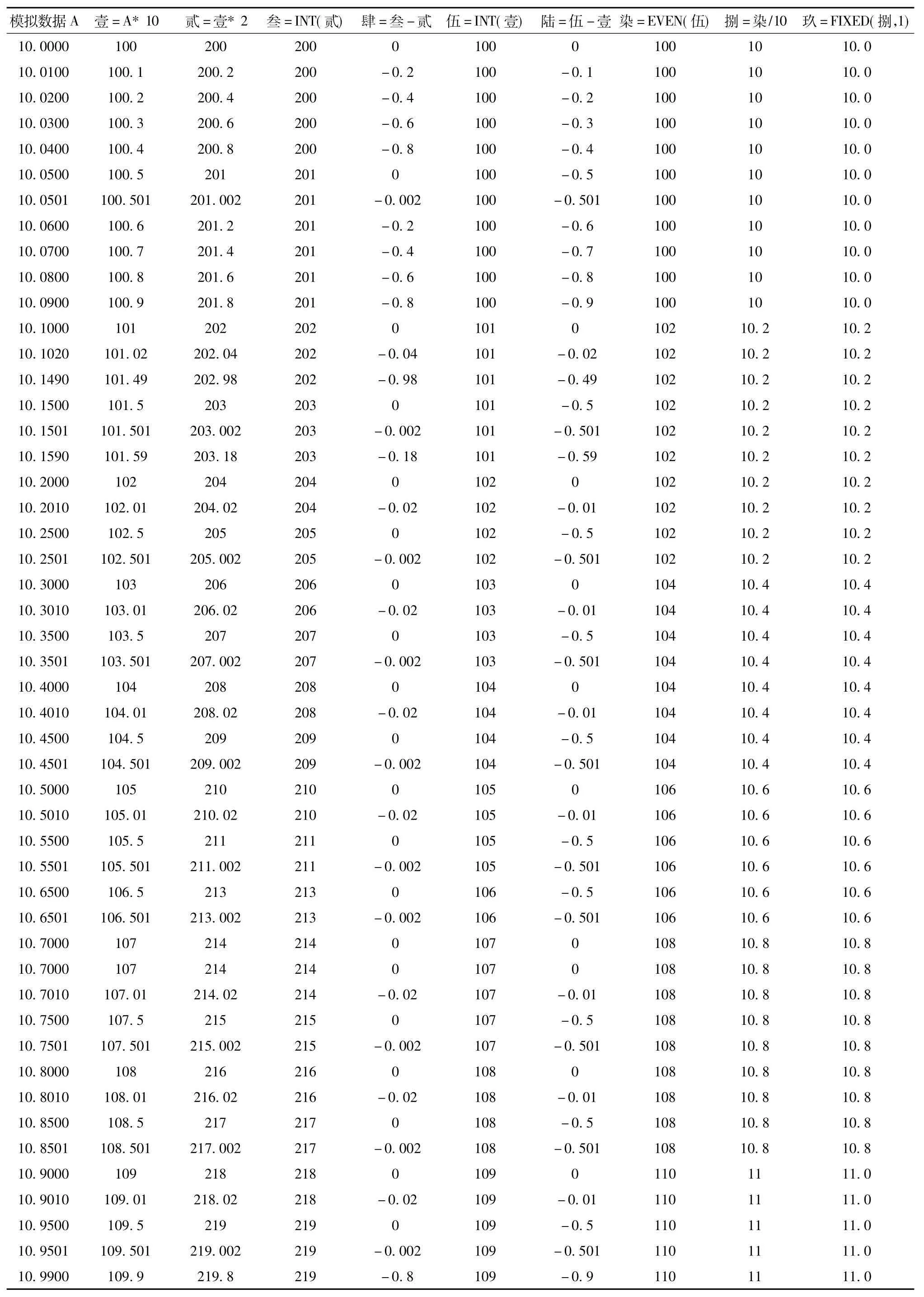
表1 数据10.00~10.99筛选处理过程
除筛选出来以外的数据,按四舍五入原则进行修约,保留两位小数。
为了使数据中的整数返回结果为小数点后两位,将结果全部按规定的位数取整。
3.3 命令的编写
综上所述,应用Excel的真假值判断函数IF、条件检验函数AND、取整函数INT、向上取偶函数EVEN、四舍五入函数ROUND、按小数位数取整函数FIXED,将命令编写为:
=IF(number> =10,FIXED(IF(AND(INT(number*20) = (number*20),INT(number*10) < (number*10)),EVEN(INT(number*10))/10, ROUND(number,1)),1),FIXED(IF(AND(INT(number*200) =(number*200),INT(number*100) < (number*100)),EVEN(INT(number*100))/100,ROUND(number,2)),2))
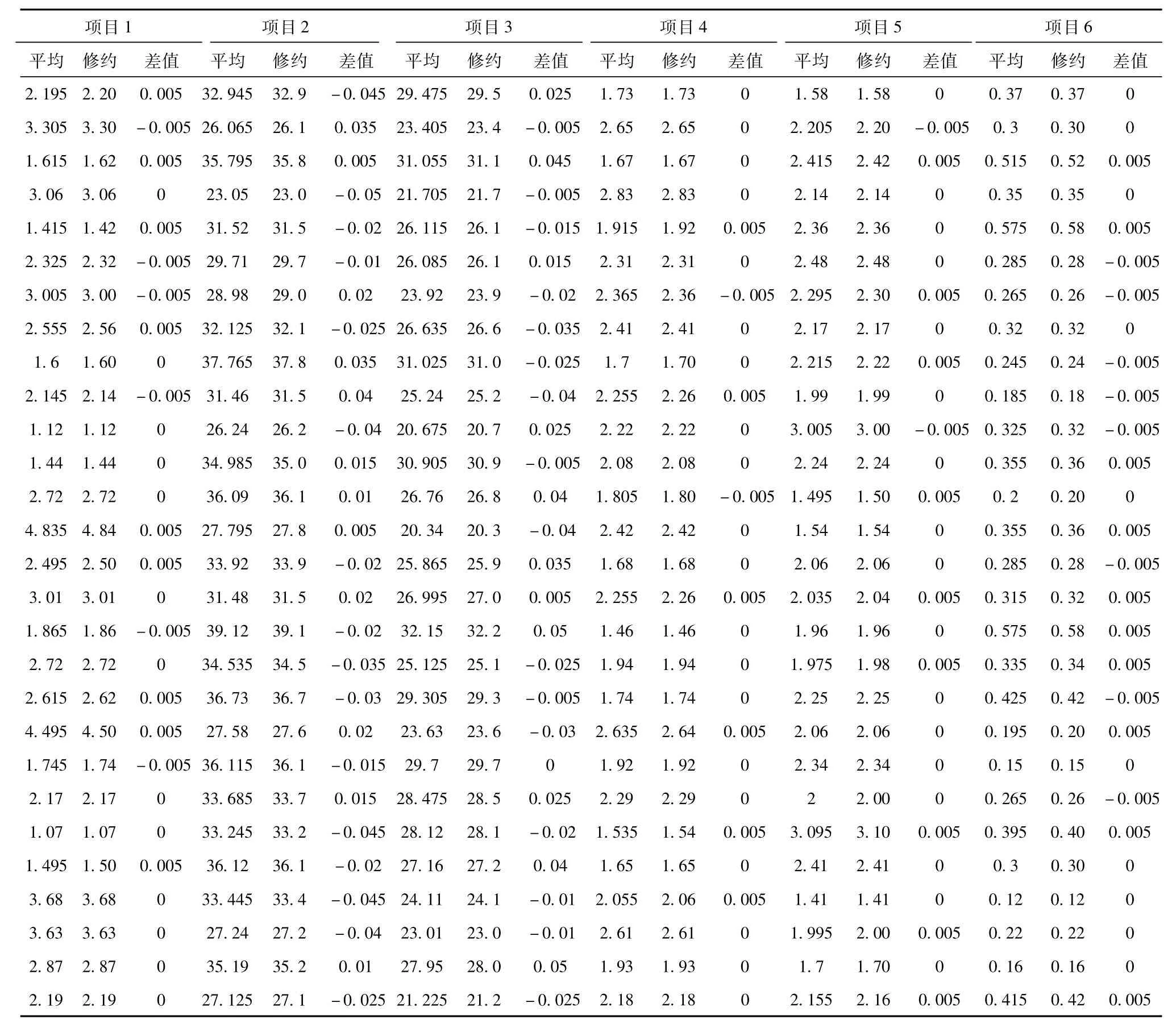
表2 所编命令在实际工作中的应用效果
即当数据≥10,如同时满足数据乘以20的结果与乘以20后取整的结果相等,并且数据乘以10取整的结果小于数据乘以10后的结果时,返回数据乘以10取整后向上取偶数再除以10的结果,如果不能同时满足条件的就返回四舍五入的结果,保留一位小数,且结果全部按保留一位小数取整;当数据不是≥10,如同时满足数据乘以200的结果与乘以200后取整的结果相等,并且数据乘以100取整的结果小于数据乘以100后的结果时,返回数据乘以100取整后向上取偶数再除以100的结果,不能同时满足条件的就返回四舍五入的结果,保留两位小数,且结果全部按保留两位小数取整。其中的number指的是数据所在单元格的位置。
4 应用验证
4.1 应用效果验证
随机抽取30个样品的180个检测平均值进行少量验证。表2给出了平均、修约和差值的统计情况,其中:平均就是各个样品各项目的检测平均值,修约就是将平均值应用所编命令处理后所得的值,差值就是修约和平均之间的差,通过差值的范围分析进或舍的情况,同时在差值一栏应用数据的筛选功能将符合五考虑原则的数据筛选出来,来检查处理后的数据是否满足我们的要求,以验证所命令的应用效果。通过人工复核后证明,应用所编命令的数据处理准确率达到100%,完全达到数据修约的规则要求。
4.2 应用稳定性验证
再将199个样品的1194个检测数据应用所编命令进行处理,以考查其稳定性。通过应用,这1194个检测数据经处理后所返回的结果完全遵守数据修约规定,数据处理的准确率达到100%,证明此命令的应用稳定性较好。
以上验证表明,此命令完全满足数据修约规则的要求,对数据的处理准确、快速,在检测数据的处理上具有较强的实用价值。
5 结论
应用 Excel中 的 IF、AND、INT、EVEN、FIXED、ROUND函数编写命令:=IF(number>=10,FIXED(IF(AND(INT(number*20) =(number*20),INT(number*10) < (number* 10)), EVEN (INT(number* 10))/10,ROUND(number,1)),1),FIXED(IF(AND(INT(number*200) = (number*200),INT(number*100) < (number*100)),EVEN(INT(number*100))/100,ROUND(number,2)),2)),可完全满足数据修约规则的要求,对数据的处理准确、稳定,具有极强的可操作性和实用价值。
[1]GB/T8170-2008,数据修约规则与极限数值的表示和判定[S].
[2]YC/T 159-2002,烟草及烟草制品 水溶性糖的测定 连续流动分析法 [S].
[3]YC/T 160-2002,烟草及烟草制品总植物碱的测定连续流动分析法 [S].
[4]YC/T 161-2002,烟草及烟草制品 总氮的测定 连续流动分析法 [S].
[5]YC/T 162-2002,烟草及烟草制品 氯的测定 连续流动分析法[S].
[6]YC/T 217-2007,烟草及烟草制品钾的测定连续流动分析法[S].
