Logistic模型的几何凸性、弹性及其应用

汪维刚

(桐城师范高等专科学校理工系，安徽桐城231402)

1．Logistic模型的几何凸性、弹性

1．1 模型简介

它是Malthus模型的拓展。该模型:N=N0en，与实际情况不够吻合，为此，修改之，设r与N有关，不妨简单设为 r(N)=r－ kN，由此得到 Logistic 模型。［1］

1．2 几何凸性

1．2．1 几何凸函数的概念

定义 设f(x)在区间I上有定义，如果对于任意x1那么称f(x)是I上的几何凸函数。

1．2．2 几何凸函数的几个性质

性质1 若g:(c，d)→(－∞，+∞)是连续的凸函数，则f(x)=eg(lnx)是(ec，ed)上的几何凸函数。(证明见文献［2］)

性质2 设(a，b)⊂(0，+∞)，f:(a，b)→(0，+∞)，f则当

x(f(x)f″(x) －(f′(x))2)+f(x)f′(x)≥0 时，f(x)是几何凸函数(不等式反向时，f(x)为几何凹函数)，反之亦然。(证明见文献［2］)

性质3 几何凸函数的倒数是几何凹函数。［2］

性质4 kf(x)(k＞0)与f(x)有相同的几何凹凸性。［3］

1．2．3 Logistic 模型的几何凸性

Logistic模型的一般形式为:

1．3 弹性［4］

1．3．1 弹性概念

f(x)的弹性是指函数的相对改变量与自变量的相对改变量的比值的极限，反映f(x)对x的变化的反应的强烈程度和灵敏度。其计算公式为:

1．3．2 弹性性质

定理 设(a，b)⊂(0，+∞)，f:(a，b)→(0，+∞)，f二阶可导，则 f(x)是几何凸(凹)函数的充要条件是f(x)的弹性是单调增加(减少)的。

1．3．3 Logistic 模型的弹性

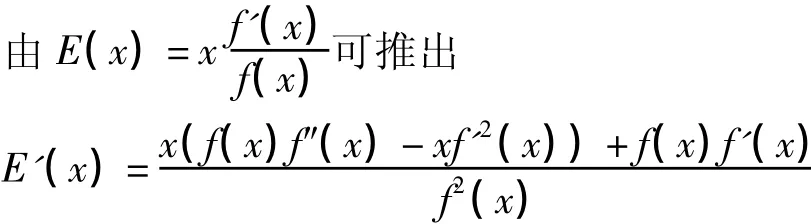
若 f(x)的弹性单调增加，则 E′(x)≥0，则 x(f(x)f″(x) －(f′(x))2)+f(x)f′(x)≥0，则 f(x)是几何凸函数。

若 x(f(x)f″(x) － (f′(x))2)+f(x)f′(x)≥0，则 E′(x)≥0，则 f(x)的弹性单调增加。

而Logistic模型为几何凸函数(见上面证明)，所以Logistic模型的弹性单调增加。

2．Logistic模型几何凸性、弹性的应用

2．1 人口预测问题［5］

首先，国策之英明，解决了中国的生存大问题，试想若没有解决好这个问题，国家谈何发展，更谈不上抓住机遇，为人类做出自己更大的贡献。但是，现在的国情有所变化，那就是，人口老年化步伐越来越快，根据最近几次的人口普查资料，发现几乎符合Logistic模型，在这里，是凸函数，所以根据“几何凸(凹)函数的充要条件是f(x)的弹性是单调增加(减少)的”的性质得知其弹性单调增加。弹性反映Logistic模型函数对变量时间t的变化的反应的强烈程度和灵敏度，随着时间的推移，人口老年率将越来越大，势必影响国家的长治久富久强，人口老年化到达一定程度，甚至连非老年人创造的财富和国家积余财富之和都将不能承受。为此，只有降低老年率，而降低老年率的有效措施就是增加非老年人，从国外输入人口是不现实的，因为中国人口基数仍然是很大的，所以笔者认为，从现在开始可以在全国范围内，暂时改变计划生育政策，那就是允许国家工作人员可以生二胎，一段时间后，必将减慢老年化步伐，虽然人口总数在上涨，但只要在国家资源所能承受范围内，还是可以执行的。(考虑到国家人口基数较大，所以现在这三十年内还不能允许生三胎。)

2．2 房价预测问题

对当前热门话题之一——房价问题，笔者谈谈一些想法:根据最近几次的房地产行情调查资料［6］，发现几乎符合Logistic模型，如果房子需求函数符合Logistic模型，就可以利用几何凸性与弹性的关系，即“几何凸(凹)函数的充要条件是f(x)的弹性是单调增加(减少)的。”

如果房子供给函数符合Logistic模型，就可以利用几何凸性与弹性的关系，即“几何凸(凹)函数的充要条件是f(x)的弹性是单调增加(减少)的。”在这里，它是凸函数，所以弹性单调增加。所以大中城市地区房地产开发，可以采取价格递减策略，因为该模型弹性是单调增加的，这样供给对价格变动的反应灵敏度就大，从而就必然有不少供给者的退出开发行为发生，从而使房地产产业发展与国家的民生政策处在一个平衡点上。

［1］张学良．Malthus和Logistic模型及其医学应用［J］．数理医药学杂志，2008(5)．

［2］郑宁国．趋势外推法数学模型的几何凸性分析［J］．高等数学研究，2007(1)．

［3］李世杰，张小明．关于连续函数的T几何凸性问题［J］．浙江万里学院学报，2006(2)．

［4］黄金莹．弹性函数的运算性质及其应用［J］．佳木斯大学学报:自然科学版，2005(1)．

［5］陈汝栋，于延荣．数学模型与数学建模［M］．北京:国防工业出版社，2006．

［6］魏巍贤，李阳．我国房地产需求的地区差异分析［J］．统计研究，2005(9):56－60．

［7］赵树嫄，胡显佑，陆启良．微积分学习与考试指导［M］．北京:中国人民大学出版社，1997．