真空平板玻璃静态与模态响应的有限元分析

缪 宏，张瑞宏，左敦稳，王洪亮，王海耀

（1.扬州大学 机械工程学院，江苏 扬州 225127；2.南京航空航天大学 机电学院，南京 210016）

真空平板玻璃作为目前世界各国刚刚兴起的一种新型节能型透明保温材料，以其优良的抗老化、保温、可见光透过和红外光反射等性能而独占鳌头，而且真空平板玻璃还是我国玻璃工业中为数不多的具有自主知识产权的前沿产品，它的研发推广既符合我国鼓励自主创新的政策，也满足当前国家对节能减排的重大战略需求，具有良好的发展前景，因此成为国内外玻璃加工技术的研究热点.［1－4］真空平板玻璃在实际使用中会受到各种载荷的作用，这些都会对其结构破坏及使用特性产生影响，因此在设计阶段必须对真空平板玻璃的模态与动态固有特性进行分析.由于真空玻璃制造技术的高难度以及掌握该制造技术的人数甚微，故目前主要集中在对真空平板玻璃的支撑应力［5－8］、封边残余应力［9］与传热机理［10－12］等方面的研究，其制造和设计理论均未系统建立，该领域的理论研究还处于起步和探索阶段，相关成果较少.本文以扬州大学提出的真空熔接法侧边封接真空平板玻璃为例，运用ANSYS有限元分析软件建立真空平板玻璃的简化模型，进行了真空平板玻璃静态与模态特性的研究.

1 真空平板玻璃的结构

真空平板玻璃采用2块尺寸为800mm×600mm的普通钠钙玻璃，单块玻璃厚度为4mm，各支撑柱之间间隔距离为10～40mm，支撑柱的直径为0.6～1.2mm，支撑柱的高度为0.2～0.5mm.首先将两块玻璃洗净，在其中一块玻璃上以一定间距放置支撑柱，然后再放上另一块玻璃，两块玻璃的四周均涂上焊接玻璃，在450℃的真空环境中加热15～60min，以去除玻璃表面附着的水分及有机物，同时用焊接玻璃将两块玻璃板的四周封边，形成一个整体.［1－4］真空平板玻璃的结构如图1所示.

2 有限元列式

将真空平板玻璃的矩形玻璃面板进行有限元分析，可以选用矩形单元对玻璃面板离散化.［7－8］为了对支承点边界处的圆孔进行模拟，在孔边可采用三角形单元.

2.1 矩形单元的位移模式

将平板中面用一系列矩形单元进行划分，得到一个离散的系统以代替原来的平板.欲使各单元至少在节点上有挠度及其斜率的连续性，必须把挠度及其在x，y方向的一阶偏导数指定为节点位移（或称广义位移）.通常将节点i的位移写成

图1 真空平板玻璃结构图Fig.1 The structure of the vacuum plate glass

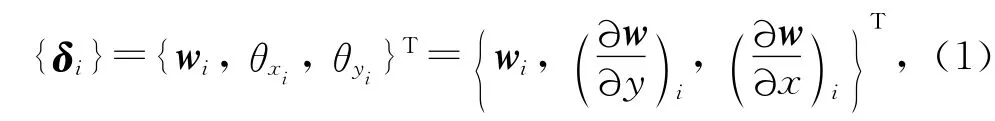
与其对应的节点力列阵是

对于矩形单元，引入一个自然坐标系Oξη来研究单元特性.由于矩形单元的每个节点有3个位移分量，一个4节点单元共有12个节点位移分量，因此选取含有12个参数的多项式作为位移模式，即

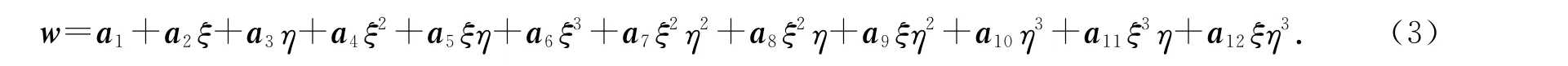
按照式（3）可得出转角，将矩形单元的4个节点坐标分别代入，求出12个参数，从而可将位移函数改写成

其中［D］为形函数矩阵，是面积坐标的函数.

2.2 矩形单元刚度矩阵的计算

式（4）代入方程（2），可以将单元应变用节点位移列阵表示为

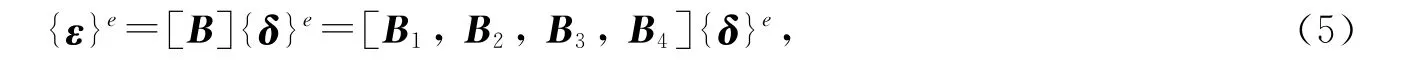
其中［B］矩阵可由［D］矩阵求出.内力－位移关系式为

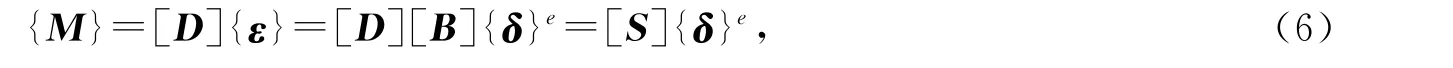
其中［S］＝［D］［B］称为内力矩阵.根据虚功原理可导出｛F｝e＝［K］e｛δ｝e，其中［K］e称为单元刚度矩阵，可以写成分块形式，其子矩阵的公式为

2.3 等效节点载荷和内力的计算

当单元上均布法向载荷作用时，等效节点载荷为

至此，已知每个节点的等效节点载荷，就可进行弯曲应力计算.计算过程如下：首先，由式（8）得到每个单元上4个节点的等效节点载荷，设真空平板玻璃板共有N个节点，然后按节点叠加成玻璃板每个节点的等效载荷，即｛R｝＝∑e｛R｝e；求出总刚度矩阵为｛K｝＝∑e｛K｝e；总节点位移向量为｛δ｝＝［［δ1］，［δ2］，…，［δN］］T；然后求解线性方程组：｛K｝｛δ｝＝｛R｝.在得到每个节点的位移值后，可按式（6）求出单元应力.

三角形单元的求解过程基本上与矩形单元相同，仅仅是位移函数选择不同：

3 有限元模型

由于真空平板玻璃的有限元模型采用实体建模时模型及其计算量很大，计算机不能实现求解，因此本文采用节点法建立简化模型.为了方便建模，采用ANSYS软件默认的笛卡尔坐标系作为建立模型的坐标系，即水平面为xz平面，竖直方向是y轴方向.由于真空平板玻璃几何对称，故将真空平板玻璃的几何中心设为模型的坐标原点.根据真空平板玻璃的材料特性及其形状尺寸，玻璃板选用壳单元SHELL63，支撑柱采用梁单元BEAM188，选择各向同性材料弹性模量为55GPa，泊松比为0.25，密度为2 500kg·m－3.先对两壳单元按40mm间距（支撑柱间距）划分网格，采用梁单元连接各节点构成支撑柱；然后对两块壳单元进行网格细化，以提高计算精度.模型采用四边夹支，这类似于真空平板玻璃正常使用时柔性夹支的工况.根据真空平板玻璃的材料特性及其形状尺寸，网格划分后共有节点36 174个，单元35 741个.

4 有限元分析结果

4.1 静态载荷作用下真空平板玻璃的应力应变

真空平板玻璃承受静态载荷（包括均布载荷和集中载荷）作用时，上下两块玻璃板的挠度差别不大.受均布载荷时，上下两块玻璃板的应力差也不大，但是当其受集中载荷时，在载荷作用区域上下两块玻璃的应力分布有较大差别，故须分别进行分析.

将真空平板玻璃有限元模型添加边界约束条件（四边夹支），在上玻璃面板上施加均布载荷，以1 000Pa为例通过有限元分析求解，可得出真空平板玻璃整体各部分的应力应变云图.

图2为均布1 000Pa时上、下板的应力云图.由图2可知，真空平板玻璃在承受1 000Pa均布载荷时，对于上玻璃板，最大应力出现在长边中心，最大应力值为4.18MPa，最大挠度值为0.40mm；对于下玻璃板，最大应力也出现在长边中心，最大应力值为4.09MPa，最大挠度值为0.39mm.

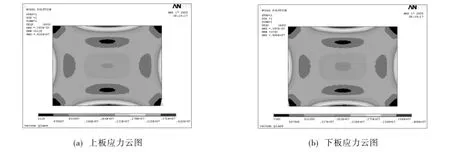
图2 均布1 000Pa载荷时上、下板的应力云图Fig.2 Stress cloud charts of up and down glass pane under 1 000Pa uniform load

4.2 受集中载荷时的应力应变

将真空平板玻璃的有限元模型添加边界约束条件（四边夹支），对上玻璃面板中心r＝2cm圆形区域施加15kg的集中载荷，通过有限元分析求解可得出真空平板玻璃整体各部分的应力应变云图.

图3为集中15kg载荷时真空平板玻璃上、下板的应力云图.由图3可见，当真空平板玻璃在中心r＝2cm圆形区域承受15kg载荷时，上玻璃板最大应力出现在中心处，最大应力值为9.10MPa，最大挠度值为0.53mm；下玻璃板最大应力出现在面板中心与两个支撑柱接触点处，最大应力值为8.12MPa，下玻璃板中心处对应节点的应力值为5.56MPa，最大挠度值为0.52mm.

由此可见，静态载荷下真空平板玻璃中心处表面应力值与挠度变形程度较大，随着与真空平板玻璃中心处距离的增加，应力值与挠度变形呈现减小趋势.

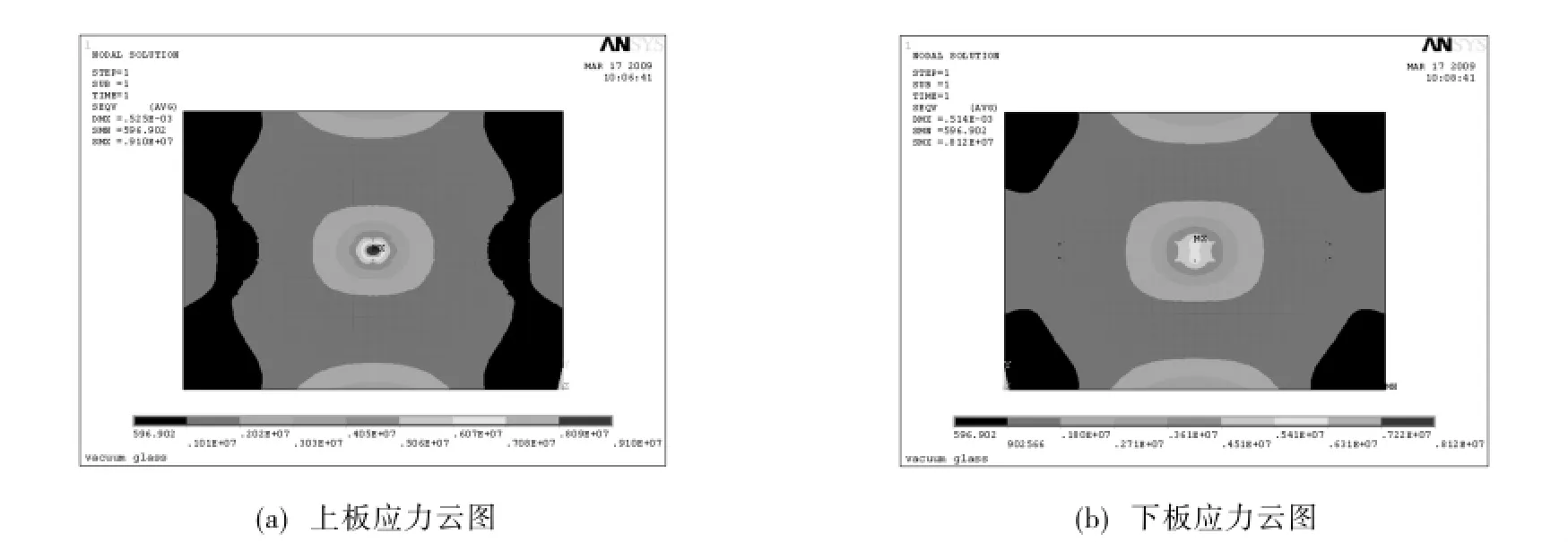
图3 集中15kg载荷时上、下板的应力云图Fig.3 Stress cloud charts of up and down glass pane under 15kg concentrated load

4.3 真空平板玻璃的模态分析

图4为真空平板玻璃模型在四边夹支条件下的前6阶振型图.由图4可见，各阶频率为1阶频率72.06Hz，2阶频率120.13Hz，3阶频率167.96Hz，4阶频率199.01Hz，5阶频率211.65Hz，6阶频率285.51Hz.真空平板玻璃在四边简支条件下的各阶振型与四边夹支条件下是完全一致的，但频率不一致，有限元分析结果为1阶频率40.21Hz，2阶频率81.29Hz，3阶频率113.33Hz，4阶频率149.71Hz，5阶频率154.12Hz，6阶频率222.09Hz.原因是真空平板玻璃的实际工况是四边柔性夹支，其支承刚度介于简支与夹支之间，同样其真实自然频率也应介于简支与夹支之间.

图4 真空平板玻璃的前6阶振型Fig.4 Preceding six modal of the vacuum plate glass

由图4可知，真空平板玻璃1阶模态为中心凸起；2阶模态为中心沿宽度方向两侧，一侧中心凸起，另一侧中心凹陷；3阶模态为中心沿长度方向两侧，一侧中心凸起，另一侧中心凹陷；4阶模态为中心凸起，两侧凹陷；5阶模态为两对角部位凸起，另两对角部位凹陷；6阶模态为一边沿长度方向两角凸起，中间凹陷，另一对边沿长度方向两角凹陷，中间凸起.

［1］ZHANG Rui－hong.Effect of surface finish of braced pillars on stress distribution of vacuum plate glass［J］.Key Eng Mater，2010，431／432：450－453.

［2］ZHANG Rui－hong，MIAO Hong，ZUO Dun－wen.Effect of heat load on the residual stress of seal edge in vacuum plate glazing［J］.Key Eng Mater，2010，426／427：81－84.

［3］王海耀.真空平板玻璃动力学研究 ［D］.扬州：扬州大学，2009.

［4］MIAO Hong，ZUO Dun－wen，ZHANG Rui－hong，et al.Effect of surface topography on stress distribution of vacuum plate glass for different aluminum alloy braced pillars［J］.Key Eng Mater，2009，407／408：705－709.

［5］张瑞宏，高建和，顾乡，等.真空平板玻璃支撑应力实验研究 ［J］.真空科学与技术学报，2006，26（6）：455－458.

［6］张瑞宏，张剑锋，王明友.陶瓷支撑柱表面形貌对真空平板玻璃应力分布的影响 ［J］.玻璃，2009（6）：38－42.

［7］缪宏，左敦稳，张瑞宏，等.MATLAB的真空平板玻璃支撑柱应力数值分析 ［J］.重庆建筑大学学报，2008，30（6）：56－60.

［8］缪宏，左敦稳，张瑞宏，等.大气压下真空平板玻璃的支撑应力 ［J］.建筑材料学报，2008，11（6）：757－761.

［9］王明友，张瑞宏，张剑峰，等.真空平板玻璃封边残余应力的研究 ［J］.玻璃钢／复合材料，2009（6）：58－61.

［10］张瑞宏，马承伟，缪宏，等.真空平板玻璃传热理论分析及试验 ［J］.农业机械学报，2006，37（12）：134－138.

［11］HAQUE M E，NEGNEVITSKY M，MUTTAQI K M.A novel control strategy for a variable speed wind turbine with a permanent magnet synchronous generator［C］／／Industry Applications Society Annual Meeting.Edmonton，Alta：IEEE，2008：1－8.

［12］DIOP A D，NICHITA C，BELHACHE J J，et al.Error evaluation for models of real time wind turbine simulators［J］.Wind Eng，2000，24（3）：203－221.