非自治广义Birkhoff系统的Poisson理论
2012-01-29龙梓轩
龙梓轩,张 毅
(苏州科技学院a.数理学院;b.土木工程学院,江苏 苏州 215009)
分析力学的Poisson理论,包括定义Poisson括号、建立第一积分的Poisson条件、由已知积分导出新的积分等是研究动力学系统的一个重要数学工具.Birkhoff力学是Hamilton力学的推广[1],Hamilton系统的Poisson理论可纳入Birkhoff系统.梅凤翔[2-3]曾研究了自治和半自治Birkhoff系统的代数结构和Poisson理论,尚玫等[4]给出广义Poisson条件以及由一个积分构造另一个积分的方法.1993年,梅凤翔[5]在Birkhoff方程的右端增加一个附加项,并称其为广义Birkhoff方程.因为通常的Birkhoff系统不容易构造,而广义Birkhoff方程的实现则较易,并且有更多的“自由度”,因此对广义Birkhoff系统动力学的研究具有重要意义.近年来,关于广义Birkhoff系统动力学的研究报道较多[6-12].在本文中,笔者拟进一步探讨非自治广义Birkhoff系统的代数结构,建立该系统的Poisson定理,并将Poisson理论推广到非自治广义Birkhoff系统,讨论与非自治广义Birkhoff系统Poisson条件相关的动力学逆问题.
1 非自治广义Birkhoff系统的代数结构
广义Birkhoff系统的运动微分方程为[5]1460
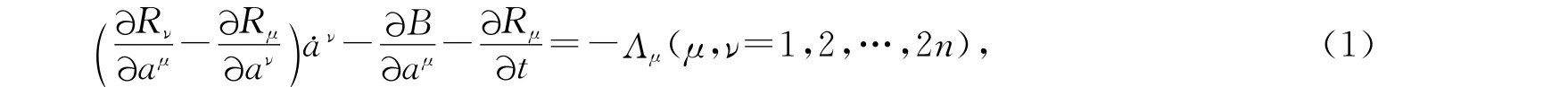
其中B=B(t,a)为Birkhoff函数,Rμ=Rμ(t,a)为Birkhoff函数组,Λμ=Λμ(t,a)为附加项.如果Birkhoff函数B,Birkhoff函数组Rμ(μ=1,…,2n)以及附加项Λμ都显含t,则称为非自治的.
将方程(1)表示为如下形式:

令

则方程(2)可表示为逆变代数形式:
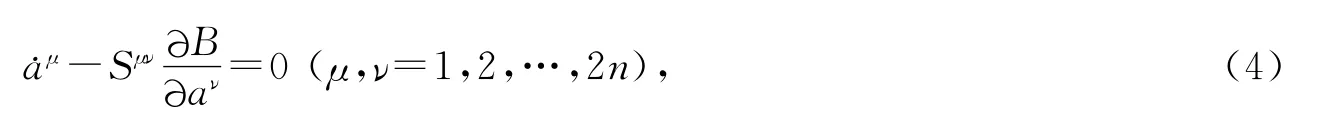
其中Sμν=Ωμν+Tμν.将某函数A(a)按方程(4)求对时间t的导数定义为一个积:

定理1 非自治广义Birkhoff系统的运动方程(1)具有相容代数结构.
由积(5)定义一个新积:

它具有反对称性 [A,B]+[B,A]=0,并满足Jacobi恒等式[A,[B,C]]+[B,[C,A]]+[C,[A,B]]=0,于是有如下定理.
定理2 非自治广义Birkhoff系统的运动方程(1)具有Lie容许代数结构.
2 非自治广义Birkhoff系统的Poisson理论
如果I(t,a)=c是系统(4)的第一积分,则有
亚里士多德指出,为了使自己说的话听起来可信,演说者在运用技巧的时候“必须把他们的手法遮掩起来,使他们的话显得自然而不矫揉造作;话要说得自然才有说服力,矫揉造作适得其反,因为人们疑心说话的人在捣鬼,就像疑心酒里搀了水一样”。[10]谭恩美并没有经历过小说中母亲们在旧中国的悲惨遭遇,为了让小说故事显得更加自然并且让人信服,她使用了讲述故事的言说技巧,让小说人物亲自讲述自己的生平经历,并用大量细节描写展现了人物的所见所闻、所思所想,使得故事更加真实、分外感人。
反之,如果I满足式(7),则I必是广义Birkhoff系统的积分.式(7)称为广义Birkhoff系统的Poisson条件,于是有如下定理.
定理3 I=I(t,a)是非自治广义Birkhoff系统(4)的第一积分的充分必要条件是式(7).
将Poisson条件(7)对t求偏导数,得到

如果Sμν(∂B/∂aν)不显含t,则式(8)成为

这表明∂I/∂t是系统的第一积分,于是有如下定理.
定理4 如果非自治广义Birkhoff系统(4)有包含时间t的第一积分I=I(t,a),而Sμν(∂B/∂aν)不显含t,那么∂I/∂t,∂2I/∂t2,…都是系统的第一积分.
同样,将Poisson条件(7)对aρ求偏导数,得到

如果Sμν(∂B/∂aν)不显含aρ,则式(10)成为

这表明∂I/∂aρ是系统的第一积分,于是有如下定理.
定理5 如果非自治广义Birkhoff系统(4)有包含变量aρ的第一积分I=I(t,a),而Sμν(∂B/∂aν)不显含aρ,那么∂I/∂aρ,∂2I/∂aρ2,…都是系统的第一积分.
定理3~5构成了广义Birkhoff系统的Poisson理论.用定理3可以判断第一积分,用定理4和定理5可以由已知第一积分导出新的第一积分.
3 非自治广义Birkhoff系统的广义Poisson方法与动力学逆问题
动力学逆问题是经典力学的主要问题之一,梅凤翔在其专著[13]中进行了系统深入的研究.与非自治广义Birkhoff系统的Poisson条件相关的动力学逆问题的提法如下:根据已知第一积分

来求非自治广义Birkhoff系统中的动力学函数Rμ,B和Λμ.
为解上述逆问题,须将第一积分(12)代入Poisson条件(7)中,得到关于Rμ,B和Λμ的一个偏微分方程,再由这个偏微分方程找到这(2n+1)个函数.显然,这类逆问题没有唯一解.
4 算例
例1 某四阶非自治广义Birkhoff系统为

已知系统的一个第一积分为

试证明∂I/∂a2,∂2I/∂(a2)2,… 都是该系统的第一积分.
由式(13)和(14)得
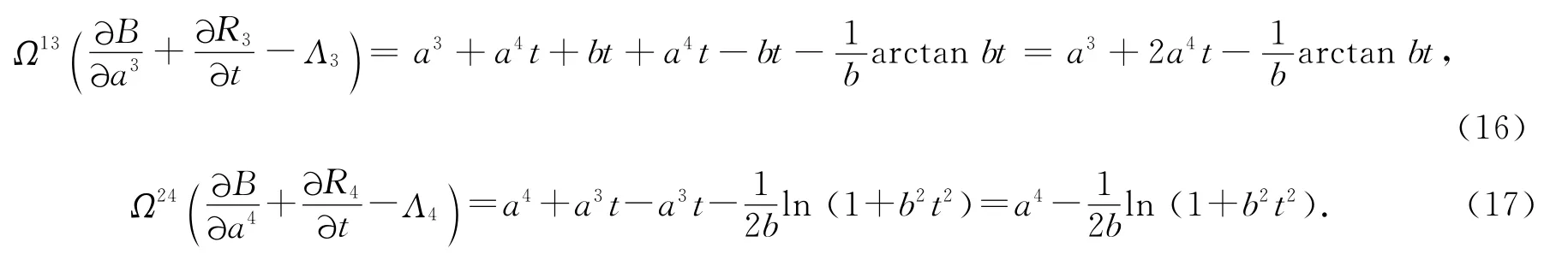
式(15)是包含变量a2的第一积分,而式(16),(17)都不显含a2,由定理5得

都是该系统的第一积分.
例2 已知某二阶非自治广义Birkhoff系统的一个第一积分

试求系统的动力学函数R1,R2,B,Λ1和Λ2.
将式(18)代入Poisson条件(7)中,得到

偏微分方程(19)中有5个未知数R1,R2,B,Λ1和Λ2,因此没有唯一解.现在取

则Ω12=-Ω21=t-2.此时方程式(19)成为

由此可得

式(20),(21)给出了该问题的一个解.
[1]SANTILLI R M.Foundations of theoretical mechanics II Birkhoffian generalizations of hamiltonian mechanics[M].New York:Springer-Verlag,1983:110-280.
[2]MEI Feng-xiang.Poisson’s theory of Birkhoffian system [J].Chin Sci Bull,1996,41(8):641.
[3]MEI Feng-xiang.On the Birkhoffian mechanics[J].Int J Non-linear Mech,2001,36(5):817-834.
[4]SHANG Mei,MEI Feng-xiang.Poisson theory of generalized Birkhoff equations[J].Chin Phys B,2009,18(8):3155-3157.
[5]MEI Feng-xiang.The Noether’s theory of Birkhoffian systems[J].Sci China:Ser A,1993,36(12):1456-1467.
[6]梅凤翔,张永发,何光,等.广义Birkhoff系统动力学的基本框架 [J].北京理工大学学报,2007,27(12):1035-1038.
[7]MEI Feng-xiang,XIE Jia-fang,GANG Tie-qiang.A conformal invariance for generalized Birkhoff equations[J].Acta Mech Sin,2008,24(5):583-585.
[8]ZHANG Yi.Integrating factors and conservation laws of generalized Birkhoff system dynamics in event space[J].Commun Theor Phys,2009,51(6):1078-1082.
[9]LI Yan-min.Lie symmetries,perturbation to symmetries and adiabatic invariants of a generalized Birkhoff system [J].Chin Phys Lett,2010,27(1):010202:1-4.
[10]ZHANG Yi.Symmetries and conserved quantities of generalized Birkhoffian systems[J].J of Southeast Univ:Engl Ed,2010,26(1):146-150.
[11]LI Yan-min,MEI Feng-xiang.Stability for manifolds of equilibrium states of generalized Birkhoff system [J].Chin Phys B,2010,19(8):080302:1-3.
[12]MEI Feng-xiang,CUI Jin-chao.Lie symmetries and generalized conserved quantities for Birkhoff system [J].J Beijing Instit Tech,2011,20(3):285-288.
[13]梅凤翔.动力学逆问题 [M].北京:国防工业出版社,2009:242-294.
