强震人员损失回归预测方法①

李晓杰，姜立新，杨天青

（1.中国地震局地震预测研究所，北京 100036；2.中国地震台网中心，北京 100045）

0 引言

地震灾害损失快速评估为灾后应急救援提供决策支持。在数据量充足，数据质量可以保证的前提下，损失评估的效果依赖于地震损失预测模型，因而探讨强震人员损失预测模型具有重要的现实意义。从地震应急角度，强震人员损失快速评估为救灾资源调度和救援人员分配指明方向，从而最大限度地挽救人员生命损失，体现地震应急的核心理念［1－4］。

关于地震人员损失模型的研究，学者进行了有意义的研究并取得了一定的评估预测效果，但也存一些相关的问题。

为了对震害损失进行评估，ATC在1985年提出了基于建筑易损性分类清单的地震损失预测评估方法［5］。这种方法通过历史震例统计不同结构的建筑物在各地震动参数下出现各种损坏等级的概率，统计建筑物损坏等级与人员损失率之间的关系；利用建筑分类清单，人口分布等相关基础数据估计人员损失［6－9］。在建筑分类和人员空间分布等相关数据完备的情况下，利用这种方法对地震损失进行预测能够取得很好地效果。但此方法存在的主要问题是高质量的建筑易损性分类清单等基础资料的收集和更新困难。从地震应急的角度，收集大量的建筑易损性分类清单资料既不经济，数据质量又难以保证。

与此相比，基于历史地震数据建立地震或地震动参数与人员损失回归关系的预测方法具有其自身的优势。估计人员损失的回归分析方法是根据历史震例记录的人员损失，地震动参数，区域人口经济等数据，建立人员损失数或人员损失率与有关参数的统计回归关系。国内外学者已利用此方法建立了多种人员损失回归模型，如上世纪90年代陈颙、陈棋福等［10］提出了基于宏观易损性的地震损失评估方法；2002年Samardjieva等［11］利用震级、人口密度建立了与人员死亡数的回归关系。本文在以上研究工作的基础上，利用USGS发布的全球地震快速评估系统PAGER，以中国1970－2000年间的128条震害记录为样本建立我国东、西部区域适用的地震人员损失预测模型；并利用1980－2007年间的234条记录建立地震重伤人数和死亡人数的回归关系。

1 地震人员损失的回归模型

2007年，USGS发布了用于地震应急的全球地震快速评估系统PAGER［12］。该系统采用三种计算模型对损失进行评估，包括回归、半经验回归和分析方法等。PAGER采用的回归模型为具有收敛性的双参数对数正态分布函数。

下面简单介绍这一模型以及计算模型参数的过程。设地震人员死亡率为V，地震烈度为S，模型为

这里Φ是标准正态分布函数；θ和β是待求参数。为了估计某次地震i造成的人员损失数，令Pi（Sj）表示处在地震烈度Sj下的人口数，则地震i可能造成的死亡人数Ei可以表示为

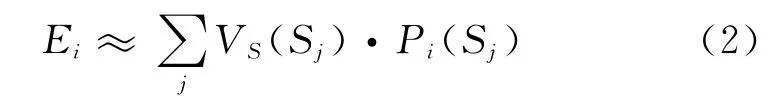
为计算模型参数θ和β使得估计人员损失值与实际人员损失值之间的残差最小，需要构建残差目标函数。由于高人员损失数的强震事件对模型结果有重要影响，为了使回归模型有很好的稳定性，可以采用如下残差目标函数：

式中Oi是地震i造成的实际人员死亡。

此外，在模型建立过程中，将会忽略掉许多对地震人员损失结果造成影响的变量，这给评估结果带来不确定性。可以采用下面的公式估计模型的不确定性ζ：

利用不确定性ζ可以计算实际死亡人数处在与模型估计值同数量级的概率。表达式为

从地震应急辅助决策的角度，地震造成的人员损失数是确定地震应急响应级别重要的参量。当利用模型估计人员损失数为e后，对于某一应急级别的阈值［a，b］，实际人员损失数d落在［a，b］内的概率为

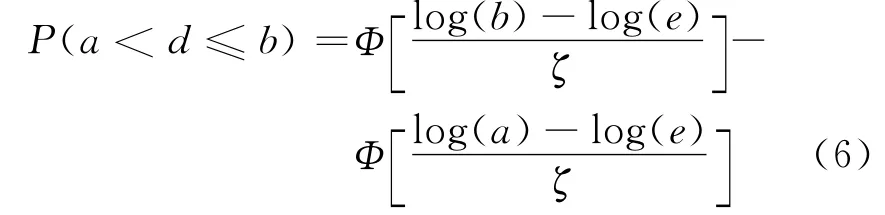
Jaiswal等［12］通过历史震例建立了区域化的模型，并对模型的拟合效果进行了检验。检验采用Lilliefors假设检验方法，检验结果认为模型残差频率分布服从对数正态分布，模型能够反映地震人员损失随地震烈度变化的规律。

建模时，此模型利用少量强震震例样本即可建立适用于不同烈度范围的地震人员损失回归模型；利用模型的不确定性及应急响应阈值可以计算实际人员损失数在某一应急响应级别内的概率；此概率可以作为判定启动应急响应级别的重要参量。

在对实际震例进行评估时，根据地震影响场以及易于获取和更新的地区人口、人口分布等数据即可对地震造成的损失进行初步估计。2008年汶川MS8.0地震15小时后，PAGER系统利用此回归模型及修正ShakeMap烈度估计可能造成的人员死亡数为50 000人，与实际灾情接近［13］。

Jaiswal等［12］利用上述模型建模时，使用仪器烈度作为模型参数，并以仪器烈度区内的人口数作为建模数据。由于仪器烈度标准与我国现场调查烈度标准不同，ShakeMap仪器烈度分布与调查烈度分布的差异及建模所采用的基础数据不同等原因，PAGER建立的人员损失模型参数不能直接用于我国地震损失快速评估工作。在我国，中国地震局在震后现场调查中以平均震害指标作为烈度判定标准勾画地震影响场，并积累了大量翔实的震后现场调查灾害资料，因而可以根据震后现场调查数据建立适用于我国地震灾害损失快速评估工作的人员损失回归模型。

本文将主要利用我国震后现场调查的震害数据构建上述人员损失回归模型，计算模型参数。

2 模型研究

2.1 数据来源及数据处理

本文选择在1970－2008年间，极震区烈度Ⅵ度以上的震例数据构造模型。数据来源包括《1990－2000中国大陆地震灾害损失评估汇编》、《中国震例》、USGS的EXPO＿2007及已发表论文中震例数据等［14－17］。根据以上数据源建立震例数据表，数据表中包含的字段分别为发震时间、震中经度、震中纬度、震级、震中烈度、各烈度区的人口数及地震造成的人员死亡数等。

由于数据来源不同，数据格式存在一定差异，因而需要进行震例筛选和数据处理。1989－2007年间发生的灾害性地震，文献中一般具有现场灾害调查记录。文献中地震影响场以现场调查烈度为依据，记录了各烈度区面积以及受灾人口总数，并未记录处于各个烈度区内的人口数以及人员损失的具体分布。对于调查烈度分布有详细记载的震例，本文利用GIS数字化，并将数字化后的烈度图与公里网格人口数据（1995，2000及2003年 GRID［18－19］，采用地区人口自然增长率［20］）进行叠加分析，统计各烈度区内人口数。对于缺乏现场调查烈度分布图，但具有各烈度区面积和总受灾人口的震例，本文按烈度区面积比例平均分配各烈度区内的受灾人口。

此外，上世纪70年代我国境内发生了几次造成重大人员损失的强震事件。为了保证模型在高烈度区的适用性，本文引用了EXPO＿2007中我国境内的个别强震数据。由于其数据格式及所依赖的基础数据及规范与我国文献中记录的数据存在一定差别，因而本文对数据进行了筛选及预处理。

本文最终选用震级范围MS4.4～7.8，震中烈度Ⅵ度以上的128个震例资料用于建模。

2.2 模型设定及数据分析

本文围绕烈度、震例空间分布与人员损失的关系进行研究讨论。

我国区域经济发展不平衡，东西部地区以及城乡之间的建筑抗震水平存在较大差异。虽然我国城乡之间的建筑抗震能力存在显著差异，但受震例样本的限制，以城乡分区方式建模还很难开展。因而本文大体按行政区划将震例数据划分为东部和西部震例两部分（1970－2008年，东部30个和西部98个震例）。所选用的震例数据的空间分布如图1所示。

从表1可知东西部地区人员损失率存在一定的差异性。本文将通过东西部分区建模与未分区建模结果进行对比，选择最优的建模结果。

2.3 模型建立及其拟合效果

本文利用Matlab及预处理后的数据构造残差目标函数，通过数值最优化算法［21］（nelder－mead algorithm）计算模型参数θ和β，进而得到人员损失率预测模型及模型不确定性。

图1 建模震例的空间分布Fig.1 Distribution of earthquakes that are used for establishing the model.

表1 东西部人员死亡率统计量定性对比

（1）1976－2007年，我国东部地区的30个震例数据得到的模型：

（2）1970－2008年间，我国西部地区的98个震例数据得到的模型：

（3）利用上述128个震例得到的不分区的人员损失率模型：

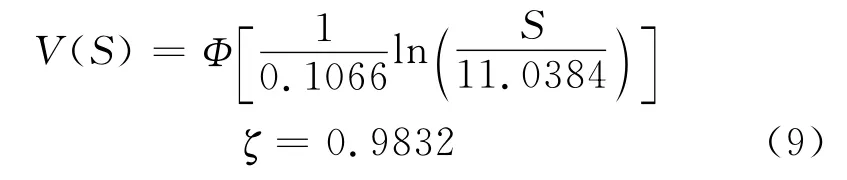
通过对分区与未分区模型的残差频率分布的正态性进行定性分析，评价模型对数据的拟合优度。残差频率分布如图2。

图2 拟合模型残差频率直方图Fig.2 Frequency histograms of fitted model residuals.

从残差频率直方图的形态可定性看出，采用东西部分区建模的残差频率正态性优于未分区模型。同时，利用SPSS软件对残差进行Kolmogorov－Smirnov假设检验表明，分区模型残差频率分布正态性优于未分区模型。此外，分区模型的残差范围明显比未分区模型残差范围小：在95%的置信区间下东部模型残差范围为（－0.224～0.494）；西部模型残差范围为（－0.439～－0.121）；未分区模型残差范围为（－1.963～－1.135）。最后，可据式（6）及不确定性ζ计算东部、西部及未分区模型各自的同量级（估计值与实际值同量级）概率分别为69%、76%和69%。

对上述模型的说明：① 模型对高人员损失数的震例事件有较高的敏感性；因而在选择震例时应该保证具有充足数量高烈度、高人员损失数的震例；②与未分区建模相比，采用分区建模能够得到更好的拟合效果；③由于东部强震震例缺乏，震中烈度Ⅸ

度及以上震例只有2个，因而东部模型需要进一步积累强震震例，提高模型的可靠性。

2.4 重伤人数估计

从地震应急角度，估计地震造成的受伤人数有利于合理调度医疗救护资源，从而提高地震应急效率和效果。

采用文献中发震时间为1980－2007年，我国范围内极震区烈度Ⅵ度以上的234个震例数据（均对重伤人数，死亡人数等有详细记录）建立震例表；然后对震例表的各个数据列进行相关性分析。分析结果表明人员重伤数与人员死亡数相关系数为0.896。

利用上述234个震例进行分析，由于在人员死亡数为0时，人员重伤数离散性很大，不利于回归。因而将数据分为震中烈度Ⅵ度以上，死亡人数为0的165震例，以及震中烈度Ⅵ度以上死亡人数不为0的69个震例。得到如下的关系：

这里Si代表重伤人数，Dn代表死亡人数，Ei代表震中烈度。

图3 构建人员重伤数模型所用震例的空间分布Fig.3 Distribution of earthquakes that are used to establish the model for estimating number of seriously injured.

3 实际震例对模型检验

本文以2008年5月12日四川汶川MS8.0地震（建模时未包括此震例）为例，对西部模型进行验证。

3.1 评估结果

（1）地震影响场。根据震后现场调查烈度分布（参照中国地震局网站）。

（2）烈度区内人口采用2003年公里网格人口数据（人口自然增长率为3‰）与烈度图层叠加，得到各烈度区人口（表2）。

表2 各烈度区人口数（单位：人）

（3）模型计算人员损失见表3和图4（估计人员死亡数与实际人员死亡数同量级概率76%）。

表3 估计各烈度区人员死亡数（单位：人）

（4）根据公式（10）估计人员重伤数约为419 100人。

（5）启动应急响应的级别。利用公式（8）及《国家地震应急预案》计算实际人员损失处在各应急响应级别内的概率。处在I级响应概率为1，启动一级应急预案。

（6）实际灾情中死亡人数69 227人，失踪18 194人；受伤人数375 783人。估计值中人员损失总数与实际损失数符合较好。

3.2 对评估结果的说明

对比实际人员损失与模型估计人员损失可以发现以下特点：① 在低烈度区模型估计人员损失值偏小，高烈度区人员损失估计值偏大。虽然在计算模型参数时采用了抑制高人员损失震例的残差目标函数，但高人员损失的震例对构建模型的影响仍然较大，因而需要在以后研究中积累强震震例对模型进行修正。② 在地震影响场比较精确的条件下，采用此模型能够近似估计人员死亡总数，估计值与实际值同量级（数万到数十万）的概率约为70%左右。③人员重伤回归表达式能够合理估计地震造成的人员受伤数。

4 总结

图4 2008年汶川地震各烈度区估计人员损失及分布Fig.4 Distribution of the eatimated casualties in different intensity areas in 2008Wenchuan earthquake.

为满足强震风险分析及地震应急工作对损失评估模型简洁性、经济性和高效性的要求，本文根据PAGER系统中的地震人员损失回归模型，利用我国地震灾害现场调查的记录数据，构建了我国东西部地区区域适用的人员损失模型。最后本文利用此模型对2008年汶川地震的人员损失进行估计，得到了接近实际震害的评估结果。另一方面，在建模过程中可以发现模型对高人员损失数的强震事件敏感度高，因而为了提高模型的稳定性需要积累强震震例对模型进行修正和改进。最后，地震人员损失受到很多因素影响，如发震时间、群众避险知识、次生灾害等，利用这些因素修正模型有待于进一步研究探讨。

［1］姜立新，聂高众，帅向华，等.我国地震应急指挥技术体系初探［J］.自然灾害学报，2003.12（2）：1－6.

［2］帅向华，姜立新，王栋梁.国家地震应急指挥软件系统研究［J］.自然灾害学报，2009.18（3）：99－104.

［3］帅向华.地震应急信息管理技术研究和指挥首长信息查询系统实现［J］.地震，2006.26（3）：93－98.

［4］帅向华，姜立新，成小平.利用WebGIS实现地震灾害信息数据的管理［J］.自然灾害学报，2003.12（3）：110－114.

［5］Applied Technology Council.Earthquake Damage Estimation Data for California （ATC－13）［R］.Applied Technology Commission，1985：280.

［6］傅征祥，李革平.地震生命损失研究［M］.北京：地震出版社，1993.

［7］杨天青，姜立新，杨桂岭.地震人员伤亡快速评估［J］.地震地磁观测与研究，2006.27（4）：39－43.

［8］谢礼立.城市防震减灾能力的定义及评估方法［J］.西北地震学报，2005.27（4）：296－304.

［9］周中红，何少林，陈文凯.震害快速评估中基于GM（1，1）模型的人口预测［J］.西北地震学报，2009.31（1）：71－74.

［10］Chen Qifu，Chen Yong，et al.Quick and approximate estimation of earthquake loss based on macroscopic index of exposure and population distribution［J］.Natural Hazards，1997，15：217－229.

［11］Samardjieva E，Badal J.Estimation of the expected number of casualties caused by strong earthquakes［J］.Bull.Seismol.Soc.Am.，2002，92：2310－2322.

［12］Kishor Jaiswal，Wald，et al.Estimating Casualties for Large Earthquakes Worldwide Using an Empirical Approach［R］，USGS Open－File Report，2009.

［13］Porter，Jaiswal，Wald，et al.Fatality Models for the U.S.Geological Survey，s Prompt Assessment of Global Earthquakes for Response System［A］∥The 14th world conference on earthquake engineering［C］.Beijing，2008.

［14］中国地震局监测预报司.中国大陆地震灾害损失评估汇编［M］.北京：地震出版社，1996，2001.

［15］张肇诚，陈棋福，郑大林.中国震例［M］.北京：地震出版社，1988，1990，1999，2000，2002，2008.

［16］中国地震台网中心.国家地震科学数据共享中心［OL］.2010，http：／／data.earthquake.cn／index.do.

［17］TrevorI Allen，Kristin D Marano，et al.PAGER－CAT：A Composite Earthquake Catalog for Calibrating Global Fatality Models［J］.Seismological Research Letters，2009，80（1）：57－62.

［18］地球系统科学数据共享运行服务总中心.地球系统科学数据共享平台［OL］.2008，http：／／www.geodata.cn／Portal／index.jsp.

［19］江东，杨小唤，王乃斌，等.基于RS、GIS的人口空间分布研究［J］.地球科学进展，2002.17（5）：734－738.

［20］中华人民共和国统计局.中国统计年鉴［M］.北京：中国统计出版社，1999－2009.

［21］John H Mathews著，周璐（译）.数值方法（Matlab版）［M］.北京：电子工业出版社，2009.