阻尼连体结构地震响应影响参数研究①

李春锋，杜永峰，李 慧

（1.兰州理工大学防震减灾研究所，甘肃 兰州 730050；2.河西学院土木工程学院，甘肃 张掖 734000；3.西部土木工程防灾减灾教育部工程研究中心，甘肃 兰州 730050）

0 引言

随着建筑多功能发展的需要，高层连体结构作为一种典型的复杂高层建筑结构，其动力特性和抗震性能已引起了众多学者和工程技术人员的关注。《高层建筑混凝土结构技术规程》（JGJ3－2002）将高层连体结构列为复杂高层建筑结构，并给出了连体结构的设计条例。在前期的研究中［1－8］，针对阻尼连体结构地震响应影响参数问题进行详细讨论研究相对较少。

本文在现有研究的基础上，采用串并联质点系层模型对其进行抽象和概括，运用Newmark－β数值算法，沿连接体连接方向输入El Centro1940波进行动力时程分析，着重探讨毗邻结构自振周期比及阻尼连体刚度变化时该结构体系地震响应的变化，以供相关实际工程应用或研究参考。

1 阻尼连体结构计算模型

1.1 计算模型的建立与假定

由于高层连体结构体系的复杂性，在进行结构动力特性及地震响应分析时就必须首先对其计算模型做一定程度简化，同时还要保证其计算精度和计算速度上的平衡性。对于双轴对称或单轴对称的连体结构，当地震作用沿其对称轴方向输入时，由于惯性力既穿过结构质心又穿过刚心，只会激起结构沿该方向的水平振动。即使地震作用沿结构非对称方向输入，此时该方向的水平振动和另一个方向的平扭耦联振动相互独立，互不耦联。串并联质点系层模型是结构动力响应分析与抗震性能研究中一种较常采用的模型，它不考虑连体结构的扭转耦联特性，但由于其模型简单、计算方便同时也为很多科研工作者和工程设计人员所熟识而较常采用。鉴于此，本文采用该模型对阻尼连体结构做毗邻结构自振周期比及连体阻尼刚度变化情形下的抗震性能研究。

1.2 振动方程的建立

假定左塔楼层数为n1，层j质量和层间刚度分别为m1j和k1j；右塔楼层数为n2，层j质量和层间刚度分别为m2j和k2j，连接体层数为T，每层质量为mL，轴向刚度为kd。连体结构示意图如图1所示，连接体与左塔铰接并认为其具有相同的运动，计算中将连接体的质量积聚到铰接端楼层，本文给定模型均假定右塔楼刚度不大于左塔楼。在水平地震作用下，阻尼连体结构的运动微分方程统一表述成如下形式：

图1 阻尼连体结构计算模型Fig.1 The calculate model for damping connective structure.

式中，［M＊］，［C＊］，［K＊］分别为连体结构的质量、刚度和阻尼的广义矩阵；X是左、右塔与地面的相对位移向量；E是单位向量；¨xg（t）为建筑物基底的有效加速度。各个矩阵分别描述如下：

式中，［M］＊L表示左塔楼质量矩阵在连体连接位置处含有连体的积聚质量。

此处［C］、［K］跟普通串联结构矩阵求解相同。根据本文模型的特点，这里仅列出图1所示连接位置处使两结构耦联的［Cd］、［Kd］矩阵即有

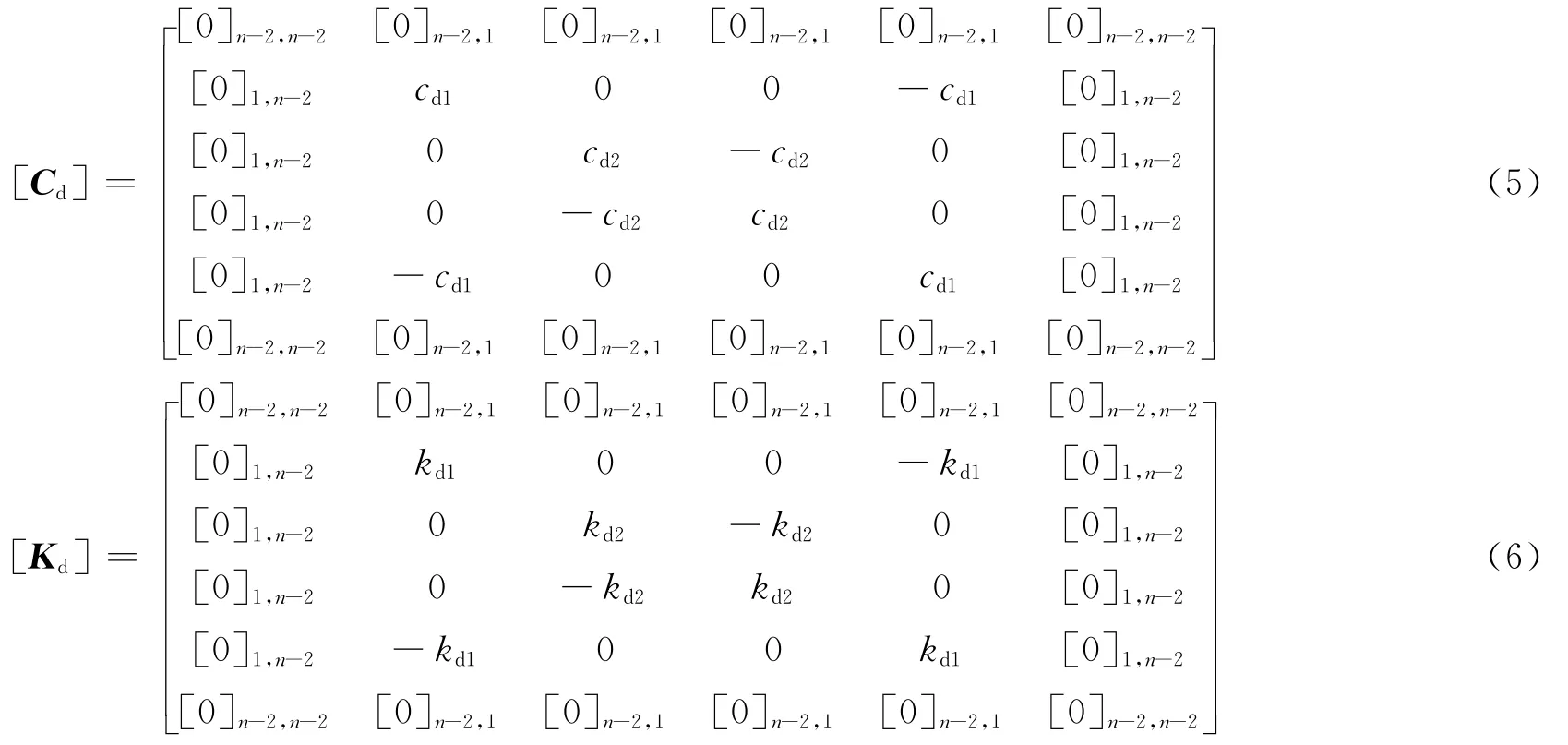
说明：在［Cd］，［Kd］中，cdi，kdj下标中1表示下层连梁的阻尼与阻尼刚度，2表示上层连梁的阻尼与阻尼刚度。

1.3 工程应用举例

两个具有相同层高2.8m，10层的相邻塔楼各自双轴对称（图1），左塔每层的质量为1.0×106kg，层间剪切刚度为4.0×109N／m，阻尼采用瑞利阻尼。2层连体设置在结构顶部，每层质量为5.0×105kg，连梁跨度10m。工程所在地的抗震设防烈度为Ⅷ度，场地土较坚硬，属于《建筑抗震设计规范》（GB50011－2001）中Ⅰ类第2组。阻尼连接时在连接体两端连梁与牛腿接触位置设置隔震橡胶垫；连接体一端与结构铰接另一端采用耗能装置（粘弹性阻尼器），阻尼器为两层粘弹性层的常用阻尼器，工作温度25℃；耗能阻尼模型采用弹簧与阻尼并联组合的Kelvin模型。右塔动力参数与阻尼器参数为后节研究地震响应影响参数值。

2 毗邻结构周期比对结构地震响应的影响

对于高层建筑，其顶部的位移是反应结构变形大小的关键参数，基底剪力在设计时也是非常重视的。所以，当毗邻结构周期比发生变化时主要对以下这些地震响应进行分析，包括顶层位移、基底剪力、楼层的层间位移、阻尼器耗能能力等。沿阻尼连接体设置方向输入的El Centro1940波（最大加速度为341.7cm／s2）并按我国规范对多遇地震的规定调幅为70cm／s2进行动力时程分析。

2.1 算例补充

为便于研究毗邻结构周期比对阻尼连体结构地震响应分析，在工程应用举例基础上对其予以补充，取左塔楼层数、层高与右塔相同，相对于左塔变化右塔楼的结构自振周期如表1所示，阻尼器参数取储能剪切模量G1＝1.50×107N／m2；损耗剪切模量G2＝2.01×107N／m2；粘弹性层剪切面积A＝0.03 m2，厚度h＝0.013m。

2.2 结构周期比对结构动力特性的影响

双塔连体结构在设置了连接体后，具有明显的平扭耦联的性质，表1列出了随着毗邻结构周期比变化时阻尼连体结构前6阶振型下的各自振周期，为便于对比在表1中列出了给定左塔前6阶振型下周期值，从中可以看出：

（1）与单体建筑相比，设置连接体后整体自振周期（对一阶振型）大于左塔自振周期（0.66s）而小于右塔，主要是由于左塔的刚度大于或等于右塔，连接体的设置使得两个单体结构的刚度得到平衡。

（2）随着周期比（右塔／左塔，长周期／短周期）值的减小，连体结构各阶自振周期逐渐减小，且振型越高，自振周期的变化越不明显。

（3）对比连接与非连接时的情形，无连接时单体结构各阶振型频率之间的差异（一阶为二阶的3倍）大于有连体时结构各阶自振频率间差异（一阶约为二阶的1.67～1.77倍），说明由于连接体的介入使得结构各振型间互相关程度加强，结构的平扭耦联程度增强，对该结构进行反应谱分析时必须采用CQC法进行计算。

表1 不同周期比下结构前6阶自振周期（s）

2.3 结构周期比对顶层位移和基底剪力影响

结构顶层最大位移和基底剪力随结构自振周期比值的影响曲线如图2所示，由图中可以看出：

（1）随着毗邻结构周期比值的增大，顶层位移变化规律为：右塔先增后减，周期比为1.58时最大为34.49mm；左塔为先减后增再减小，周期比为1.35时最小为24.03mm，周期比为1.58时最大为32.64mm；总体来说，毗邻结构周期比值越小，结构顶层位移响应应该最小，周期比为1.04时左、右塔顶层位移分别为23.96mm和23.53mm，而周期比值为1时左、右塔顶层位移出现突增，分别为30.09 mm和29.29mm，其原因是由于此时结构的自振周期为0.69s，其与输入的El Centro地震波的卓越周期近似相等而产生共振所致。

（2）基底剪力随周期比值的增大，规律为：当周期比小于1.58时，左右塔楼剪力值均为先减后增，周期比为1.35s时最小分别为1.33×104kN和9.25×103kN；当周期比大于1.58时，左塔基底剪力先减后增，右塔剪力单调减小，在周期比为1时产生剪力突变的原因与（1）相同。

2.4 结构周期比对层间位移影响

结构2、5、8、10层层间位移随周期比的影响曲线如图3所示，从图中可以看出：

图2 结构周期比对顶层位移和基底剪力影响Fig.2 The influence on the top displacement and base shear with different period ratio.

（1）对左塔，随着结构自振周期比值增加，当周期比小于1.58时层间位移均呈现先增后减的趋势，周期比为1.35时各层间位移最小；当周期比大于1.58时层间位移又出现先减后增的趋势，周期比为1.75时各层间位移最小，且这种趋势随着楼层的增加变得越来越不明显。

（2）对右塔，随着周期比的增加，2、5层层间位移呈增加趋势而8、10层层间位移呈持续下降趋势，实际设计中可依据设计规范要求取折衷。

（3）周期比为1时结构层间位移与分析出现差异的原因是由于连体结构自振周期与输入地震波卓越周期相近或相等所致。

图3 结构周期比对结构层间位移的影响Fig.3 The influence on the layer displacement with different period ratio.

2.5 结构周期比对阻尼器耗能与连梁内力影响

由于连体结构在连梁位置设置了阻尼器，连接方式属于连体结构中的弱连接形式，连梁内力主要以轴向受力为主，且其轴力主要来源于阻尼器，其内力较基底剪力等均要小的多。阻尼器的耗能能力一直以来是人们非常关心的问题，此处针对本文提出的阻尼连体结构类型一并给出其在周期变化情况下的变化规律如图4所示。从图中可以看出：随着毗邻结构自振周期的增加，阻尼器耗能能力与连梁内力均呈上升趋势，其说明连体结构由于毗邻结构非对称性加强使结构受力变得复杂，连体结构连梁受力也越大；此外从图4中可以看出，随周期比的增大，下连梁的耗能能力比上连梁的耗能能力强，且下连梁受力大于上连梁的受力。

图4 毗邻结构周期比对阻尼器耗能与连梁内力影响Fig.4 The influence on the damping dissipation and the connection beam internal force with different period ratio.

3 阻尼器参数对结构地震响应的影响

3.1 算例补充

在1.3基础上，给定右塔是与左塔层数、层高、质量均相同的结构，阻尼仍采用瑞利阻尼，阻尼器仍采用两层粘弹性层的常用阻尼器，右塔的层间剪切刚度为2.2×109N／m。

3.2 阻尼器参数分析

粘弹性阻尼器的阻尼刚度和阻尼系数分别从下式确定：

这里，A为粘弹性层面积；G1为剪力贮存模量；G2为损耗模量；hv为粘弹性层厚度；ω为结构基本自振频率。

由式（7）、（8）可得到

由式（7）～（9）可以看出，粘弹性阻尼器的设计，参数G1，G2通常由实验确定，可认为已知，阻尼器的设计可认为是阻尼刚度设计，阻尼系数可由阻尼刚度通过式（9）获得。鉴于此，此处阻尼器参数的研究将针对给定结构，讨论当阻尼器刚度变化时连体结构的动力特性与地震响应变化。

3.3 阻尼刚度对结构动力特性的影响

阻尼连体的引入，使得结构的动力特性变得比单体时复杂的多，为分析阻尼参数对结构动力特性影响，表2给出当连接体阻尼刚度发生变化时前6阶振型下结构自振周期，从表中可以看出：

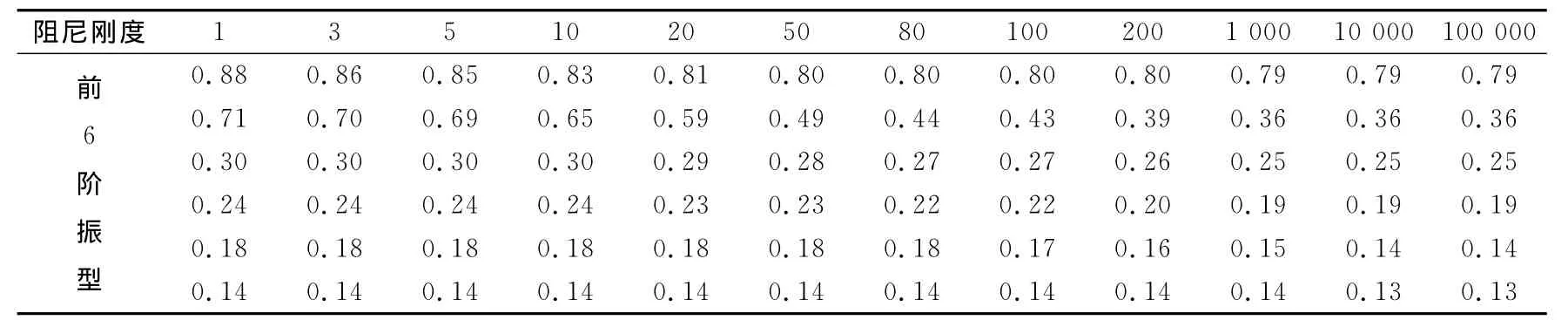
表2 不同阻尼刚度下结构前6阶自振周期（s）

（1）阻尼连体结构各振型间自振周期差异较小，说明该结构具有较强的平扭耦联特性。

（2）随着阻尼刚度值的增加，结构各振型下的自振周期逐渐减小。针对给定结构，当阻尼刚度达到一定值2×107N／m后，结构自振周期变化非常小。

3.4 阻尼刚度对结构顶层位移与基底剪力的影响

对给定连体结构，当连接体阻尼刚度发生变化时，阻尼刚度对顶层位移与基底剪力的影响如图5所示，从图中可以看出：

图5 阻尼刚度对结构顶层位移与基底剪力影响Fig.5 The influence on the top displacement and base shear with different damping stiffness.

（1）随着阻尼刚度增加，左塔顶层位移先减小后增大，至刚度为1.0×107N／m时，结构顶层位移最小为21.20mm，右塔顶层位移随阻尼刚度增加而减小，位移变化显著；阻尼刚度增加到1.0×109N／m时，左、右塔顶层位移变化不再显著。

（2）基底剪力随阻尼刚度的增加，均先减小后增大；左塔在阻尼刚度为1.0×107N／m时基底剪力最小为1.17×104kN，右塔在阻尼刚度为3.0×106N／m时基底剪力最小为9.02×103kN；当阻尼刚度达到1.0×109N／m时左塔基底剪力随刚度变化不明显，当阻尼刚度达到1.0×108N／m时右塔基底剪力随刚度变化不明显。

（3）据（1）、（2）分析可以看出针对本文给定结构当阻尼刚度取1.0×107N／m时为最优阻尼刚度；此外，阻尼系数及阻尼器参数可据式（7）～（9）算出。

3.5 阻尼刚度对结构层间位移的影响

阻尼刚度对结构层间位移的影响如图6所示，从图中可以看出：

（1）对左塔，随着阻尼刚度增大，2、5、8层各层间位移先减后增，当阻尼刚度为1.0×107N／m时各层间位移最小分别为2.86mm、2.41mm及1.77 mm，仅顶层层间位移在刚度为1.0×108N／m时最大，但仅为0.78mm。

（2）对右塔，随着阻尼刚度增加，2、10层层间位移先减后增，5、8层层间位移单调减小；其中当阻尼刚度为3.0×106N／m时2层层间位移最小为4 mm，阻尼刚度为5.0×107N／m时10层层间位移最小为0.31mm。

（3）针对阻尼连体结构层间位移，随着层高的增加，结构层间位移逐层减小；此外，当阻尼刚度达到1.0×109N／m时，左、右塔的各层间位移受阻尼刚度变化影响非常小。

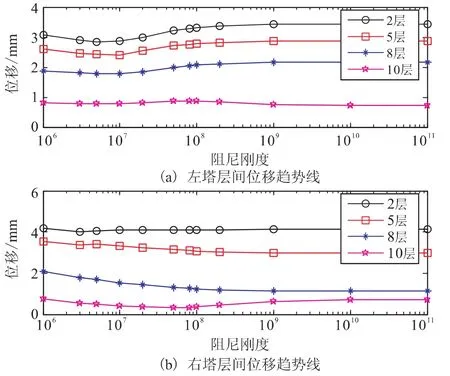
图6 阻尼刚度对结构层间位移的影响Fig.6 The influence on the layer displacement with different damping stiffness.

3.6 阻尼刚度对阻尼器耗能与连梁内力的影响

由图7可以看出，阻尼器耗能随阻尼刚度增加先增后减，当阻尼刚度为3.0×106N／m时，阻尼耗能最大；当阻尼刚度达到1.0×109N／m时，阻尼器耗能能力变的非常弱；连梁内力随阻尼刚度增加，下连梁内力单调增加，上连梁内力先增后减，在阻尼刚度达到2.0×107N／m时上连梁内力最大达到133.46kN。

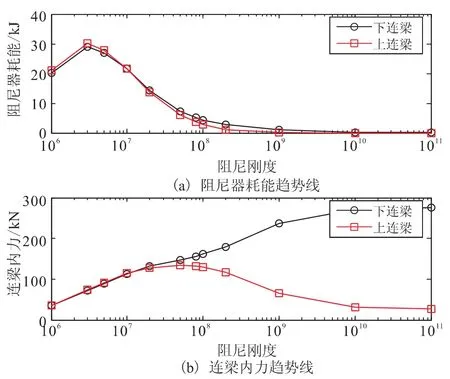
图7 阻尼刚度对阻尼器耗能与连梁内力的影响Fig.7 The influence on the damping dissipation and connection beam internal force with different damping stiffness.

4 结语

针对本文提出模型，通过上述分析，可以得出以下几点结论：

（1）随着周期比值的减小或阻尼刚度值的增加，连体结构各阶自振周期逐渐减小，且振型越高，自振周期的变化越不明显。

（2）毗邻结构周期比值越小，结构顶层位移响应越小，基底剪力随周期比的增加：左塔先增后减，右塔持续减小；随着周期比的增加，层间位移左塔先减后增，右塔下部各层间位移呈上升趋势而上部各层间位移呈下降趋势，连梁内力和阻尼器的耗能能力均随周期比的增加而变大；

（3）随着阻尼刚度增加，结构顶层位移对左塔先减后增，对右塔单调减小；基底剪力均呈先减后增趋势，但刚度位置不同；层间位移随刚度变化规律较复杂，阻尼器耗能能力及上连梁内力随刚度增加先增后减，下连梁内力随刚度增加单调增加；此外当阻尼刚度增加到一定程度时，其变化对结构地震响应的各个参数影响变的非常小。

［1］郭涛，宁娟，姚激，等.非对称大底盘双塔连体结构动力特性和地震响应分析［J］.西北地震学报，2009，31（3）：254－259.

［2］黄坤耀，孙柄楠，楼文娟.连体刚度对双塔连体高层建筑地震相应的影响［J］.建筑结构学报，2001，22（3）：21－26.

［3］Y L XU，Q HE，J M KO.Dynamic response of damper－connected adjacent buildings under earthquake excitation［J］.Engineering Structures.1999，27（21）：135－148.

［4］Jinkoo Kima，Jingook Ryua，Lan Chung.Seismic performance of structures connected by viscoelastic dampers［J］.Engineering Structures，2006，34（28）：183－195.

［5］李浩，张艳梅.利用正交多项式对三维地震资料拟合算法的研究［J］.西北地震学报，2009，31（2）：148－151.

［6］杜永峰，李春锋.阻尼连廊位置对高层连体结构地震响应的影响［J］.建筑科学，2008，（11），31－35.

［7］杜永峰，李春锋.连接体刚度对连体位移响应影响的平稳随机振动分析［J］.兰州理工大学学报，2008，34（6）：125－130.

［8］杜永峰，李春锋.连体位置对单轴对称连体结构地震响应的影响［J］.四川建筑科学研究，2009，（1）：157－160.

［9］杜永峰，李春锋.连廊位置对高层连体结构地震响应的影响［J］.工程抗震与加固改造，2008，（3）：60－63.