复合材料声发射信号传播特性试验研究

于金涛，丁明理

(1.哈尔滨商业大学 计算机信息与工程学院，黑龙江 哈尔滨150028;2.哈尔滨工业大学 自动化测试与控制系，黑龙江 哈尔滨150001)

0 引言

直升机机械部件的疲劳试验是确定直升机主要构件的使用时效，保证直升机使用安全的主要手段。在直升机部件的疲劳试验中，利用声发射技术(acoustic emission，AE)监测可以更早发现损伤的萌生、位置、类型等情况，能有效的发现损伤部位和损伤的程度。因此开展直升机机械部件声发射检测技术的研究，进一步改进和提高疲劳试验状态下损伤检测的效率和精度，对准确评估直升机各重要部件寿命及安全性是非常有意义的。

应用声发射技术对设备进行无损检测时，主要有两个方面的影响因素[1]:一个是背景噪声的干扰;另一个是波传播过程中发生衰减、反射、模式转换等使接收到的信号与声发射源信号存在差异。噪声的存在影响波形分析的可靠性，而波的传输特性是设备无损检测的基础。因此在应用声发射技术进行检测之前，必须研究波在设备上的传播特性。由于直升机部件主要采用复合材料制成，因此本文研究声发射信号在直升机常用复合材料试件上的传播特性。

大量的研究表明[2－4]，声发射信号的传播特性主要受到传输距离、结构的连续性以及复杂性等因素的影响，导致采集信号发生较大的失真。王向红和毛汉领利用小波包分析了声发射信号在水轮机上的传播特性，包括距离衰减特性和不连续界面上的衰减特性[5－6]，为水轮机裂纹声发射检测提供了基础。但是传统的小波包分析存在很多缺点:1)由于传统小波不具有理想盒形的频谱特性，造成相邻频段能量泄露;2)传统小波包频带以2的倍数划分，不能任意选取感兴趣的频带进行分析;3)每分解一层小波系数就会减半，造成不同层频率分辨率不同。以上缺点使得传统小波包分析在分析精度、使用灵活性上存在一定局限性。谐波小波具有理想盒形的频谱特性，谐波小波包分析克服了传统小波包分析的以上缺点，并且已经在旋转机械故障信号提取、故障诊断，转子轴心轨迹提取等得到了成功的应用[7－11]。因此本文利用谐波小波包分析声发射信号在直升机动部件常用复合材料试件上的传播特性，为传感器布置、声发射源定位和破损模式识别提供依据。

1 谐波小波包分析原理

1.1 谐波小波

剑桥大学的 D.E.Newland 教授[12]于1993 年从频域出发构造了具有理想盒形(Box－like)特性的谐波小波。其时域表达式为

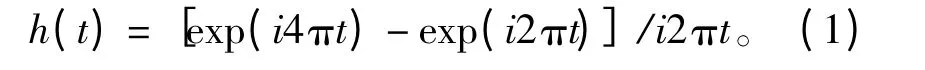
其实部、虚部如图1所示，其频谱如图2所示。从图2可以看出，谐波小波的频谱(ω)具有严格的盒形及良好的紧支撑特性。

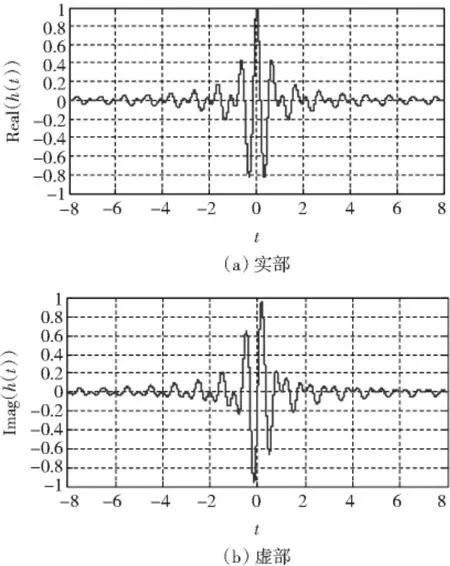
图1 谐波小波函数波形Fig.1 The real part and imaginary part waveform of harmonic wavelet

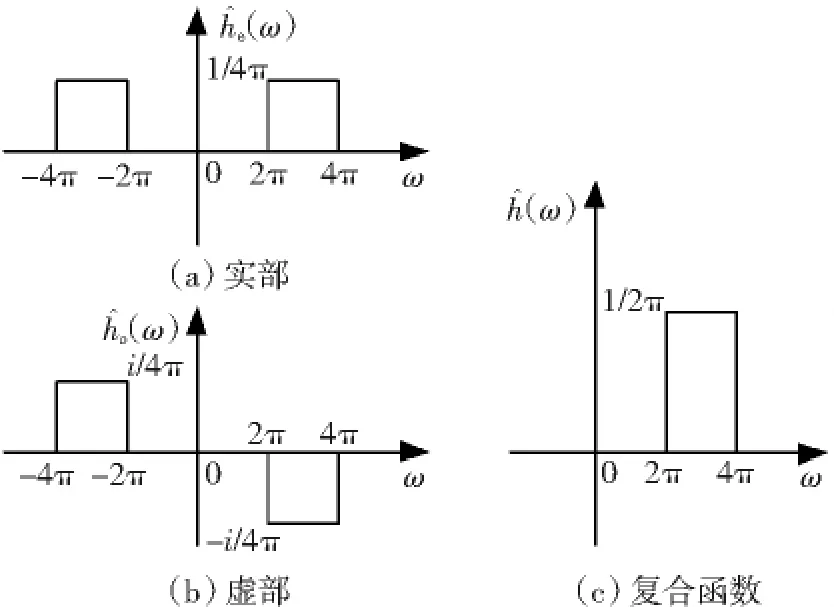
图2 谐波小波频谱Fig.2 Frequency spectrum of harmonic wavelet

用变量(2jt－k)替代式(1)中的变量t，可得

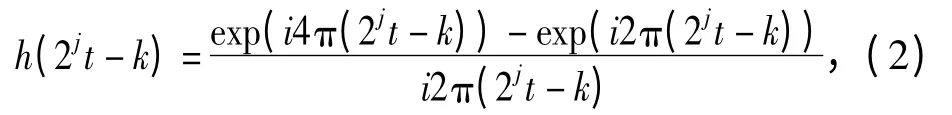
其中，j、k∈Z。可以看出，小波的形状没有改变，但他在尺度方向上压缩了2j倍，并且其位置在新的尺度上平移了k个单位。谐波小波h(t)及其伸缩平移式(2)构成L2(R)空间的规范正交基。以谐波小波作为基函数系，可将信号正交分解到相互独立的空间，将信号所含不同的频率分量分解到相对应的频段。谐波小波对信号的分解从低频到高频是以2倍的关系逐渐增加的，对信号的低频部分划分比较细，而对高频部分划分比较粗，即经典谐波小波同传统二进小波分解一样受到二进制限制。

1.2 广义谐波小波

为了使小波分解频带的选择更加灵活，Newland于1994年提出了广义谐波小波[13－14]。引入正实数m，n(m ＜n)，考察频带[m2π，n2π]，将谐波小波广义化为

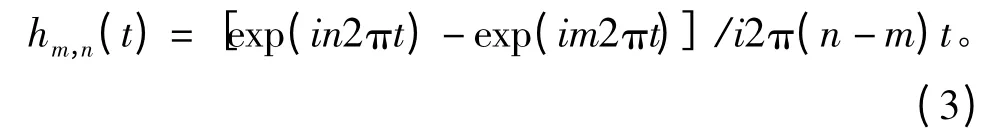
可以看出，m，n之间没有n=2m这一条件的限制，也即二进限制，只要保证m＜n即可，这就使得谐波小波在分析频带的选取上具有更大的灵活性。这就是广义谐波小波与经典谐波小波相比的一个明显优势。

给定步长 k/(n－m)，k∈Z，用 t－k/(n－m)替换 t，则可得

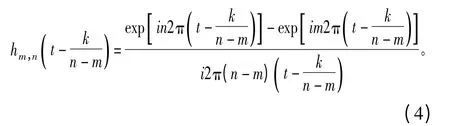
这就是分析频率带宽为(n－m)2π，分析中心在t=k/(n－m)处的广义谐波小波的一般形式。显然当 m=2j，n=2j+p(j，p∈Z+)时，即为二进经典谐波小波形式。对于离散信号 x(r)，r=0，1，2，…，N－1，其谐波小波变换为

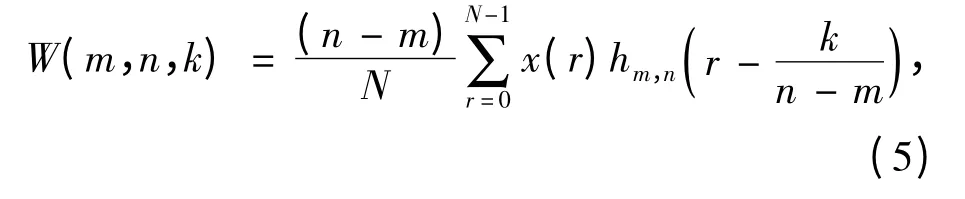
其频域表达式为

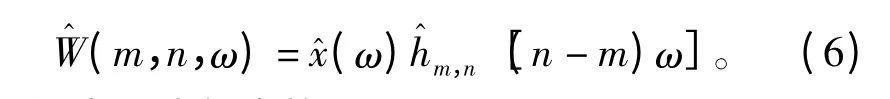
1.3 谐波小波包变换

在传统小波分析中，对低频带信号刻划精细，而对高频带信号刻划较粗。为了对整个分析频带进行任意“细化”以获取信号中的特定频率成分，这就需要采用小波包的分析思想。对于谐波小波包分解，其频带划分思想与小波包是一致的，下面介绍其具体实现过程。

由式(4)可知，广义谐波小波关键在于尺度参数m，n的选取，设信号的奈奎斯特频率为fs，则第j(j为非负整数)层各小波的分析频率带宽为

这样就可设分析频带的上、下限频率为

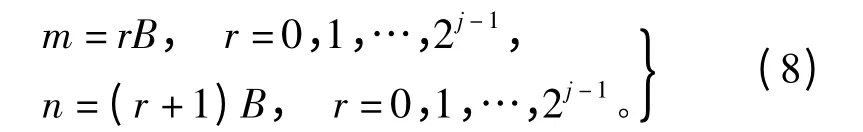
随着分解层数 j的逐渐增大，就可以应用谐波小波包对信号的整个分析频带进行“无限”的细化划分。如果对信号的某一频段感兴趣，由式(7)确定信号的分解层数j，再由式(8)确定所要分析频带的上、下限频率，也就是定义谐波小波的尺度参数m，n。这样，通过式(5)进行循环卷积计算出小波系数，就实现了相应频段上的谐波小波分解。显然信号经过小波包分解后，在各个频带中的信号仍具有与原始信号相同的频率分辨率;而且分解后信号的数据长度并不减少，克服了Mallat算法的小波包分解带来的数据长度减少的问题。

由以上的分析可知，通过有规律的调整尺度参数m，n，谐波小波可进行良好的小波包分解，谐波小波包变换的实现过程如下:

1)根据先验知识分析带宽、频段范围确定感兴趣的频率成份所在的分解层和频段值，即由式(7)计算层数j和式(8)计算尺度参数mj，nj。

2)计算谐波小波的频域频段值

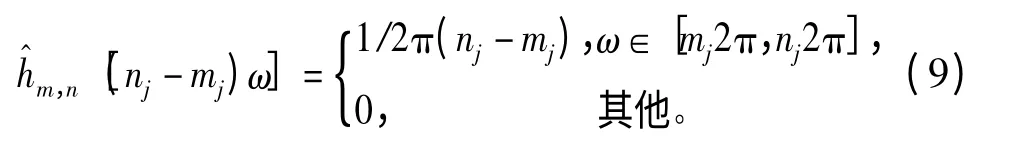
3)对离散时间序列信号 x(t)进行FFT，求取其频域离散值(ω)。

4)由式(6)计算所确定的频段的小波变换。可直接对所确定频段的变换信号进行频域特征分析。

5)进行逆FFT，得到小波变换后的时域信号，从而对所确定频段的变换信号进行时域特征分析。

2 实验研究

在直升机动部件常用的碳纤维复合材料和蜂窝复合材料上进行了传播特性试验，试件参数如表1所示。

表1 试件参数Table 1 Parameters of the testing specimens

采用德国Vallen公司的AMSY－5系统及配套设备，VS150－M宽带传感器6个，按照如图3所示坐标粘贴，图4和图5为试件1和试件2实际传感器布置图。测试系统结构如图6所示。测试信号由标准断铅实验产生。

图3 传感器粘贴坐标示意Fig.3 Coordinates schematic diagram of AE sensors

图4 试件1传感器实际布置Fig.4 The actual distribution of AE sensors on specimen 1

图5 试件2传感器实际布置Fig.5 The actual distribution of AE sensors on specimen 2

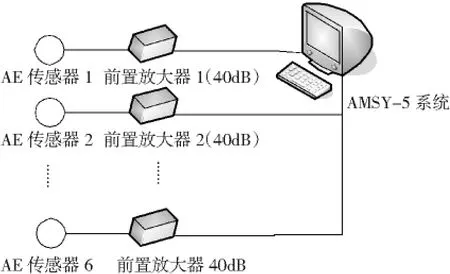
图6 测试系统示意图Fig.6 Schematic of the AE measurement system

为了减少测量误差，对2个试件分别进行了30°和80°断铅试验，每个断铅角度断铅5次，尽量保证每次断铅角度和强度相差不大。试验过程中采集系统的参数设置如表2所示。

表2 测试参数设置Table 2 Test parameters setup of AE acquisition system

3 结果与讨论

3.1 声发射参数衰减结果

选用声发射信号的能量和幅值参数来描述其衰减情况，声发射信号的能量定义为

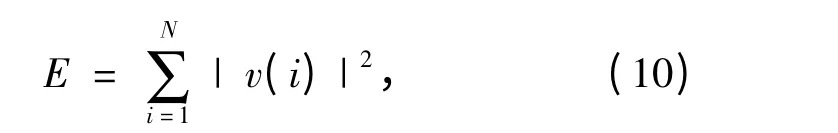
其中，v(i)是声发射信号第i个数据点的幅值。为了减少误差，对于每种试件每个角度的断铅试验，取5次结果的平均值作为测量值。以离断铅点最近的第1个传感器的AE信号作为参考，用相对衰减率描述AE信号的衰减特性，能量相对衰减率 SEj和幅值相对衰减率SAj为

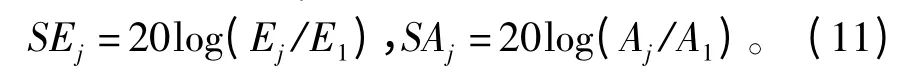
图7为试件1的能量和幅值相对衰减率和距离之间的曲线，图8为试件2的能量和幅值相对衰减率和距离之间的曲线。

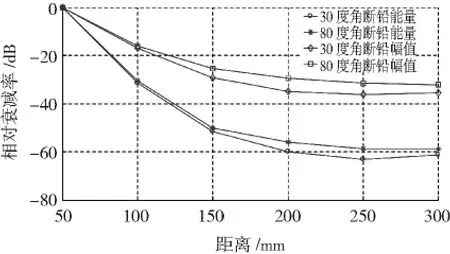
图7 试件1相对衰减率曲线Fig.7 The relative attenuation rate curve on specimen 1

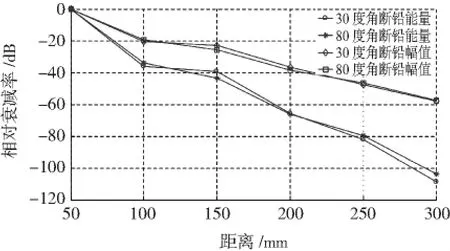
图8 试件2相对衰减率曲线Fig.8 The relative attenuation rate curve on specimen 2

通过对图7和图8分析，可以得出结论:

1)无论是试件1还是试件2，30°和 80°角断铅的能量和幅值衰减特性都是传播距离越远衰减越大，说明信号传播的距离对信号幅值和能量有较大的影响。通过本试验可以估计能被检测到损伤信号的强度，对于阈值为40 dB，从图8可以看出，对于试件2来说，经过200 mm的传播距离后，幅值相对于第一点降低了39 dB，这就要求损伤点传来的信号最小幅值应该大于79 dB，否则在200 mm外不能检测到该信号。可以根据衰减特性，设计合理的传感器阵列布置方案。

2)无论是试件1还是试件2，能量的衰减率都大于幅值的衰减率。这是由于幅值参数包含AE波形的信息比能量值小，幅值参数只是波形幅值的最大值，而能量参数是整个波形中幅值的平方和，因而能量对信号的衰减比幅值更敏感。

3)试件1在200 mm之后，幅值和能量衰减都减弱，即偏离理想衰减特性很大，这主要是由于试件边界对信号的反射叠加到原始信号上，加上随着传播距离增大，信号频散和畸变加大，使得衰减速度减弱。此时，单纯利用能量法进行定位在200 mm后将会存在很大误差。

3.2 声发射信号衰减的谐波小波包分析

以上只是从总体上分析了声发射信号在试件1和试件2上的衰减特性，为了详细分析声发射信号在各个频段的衰减特性，利用谐波小波包提取了声发射信号5个频带的信号。通过对声发射信号进行频谱分析，可以看出声发射信号的有效信息集中在500 kHz以内，因此选取5个频带为0～100 kHz，100 ～200 kHz，200 ～ 300 kHz，300 ～ 400 kHz，400～500 kHz，分别定义为频带1～频带5。很显然，利用传统小波包分解是无法精确得到这几个频带的，由于采样频率为5 MHz，因此经过4层分解只能得到以156.25 kHz为间隔的频带，由于信号长度只有2048点，每频段的小波系数只有128点，经过5层分解只能得到以78.125 kHz为间隔的频带，每频段的小波系数只有64点。利用谐波小波包只需要根据式(7)和式(8)调整 m、n，就可以精确的提取要分析的频带的信号，并且信号点数不变。

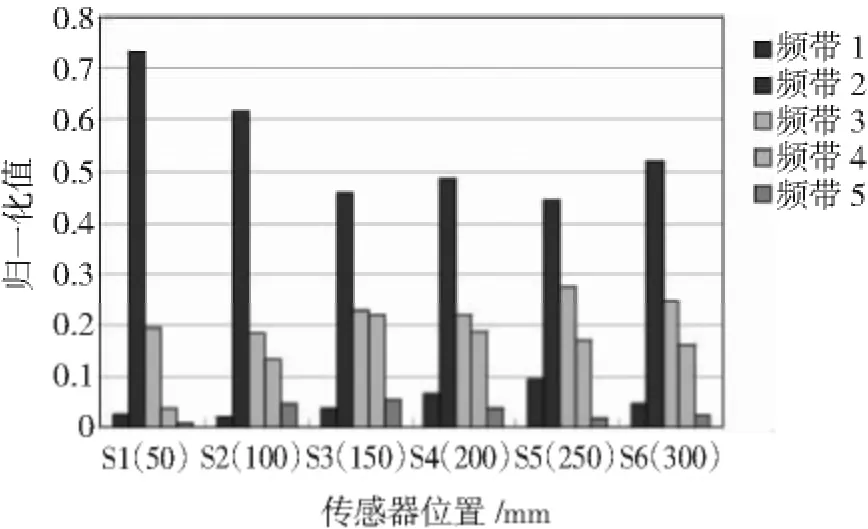
图9 试件1五个频带归一化能量图(30°角断铅)Fig.9 Normalization energy value of the five frequency bands(specimen 1 with 30°angle pencil lead break)

试件1 30°角断铅6个传感器5个频带的归一化能量如图9所示，试件2 30°角断铅6个传感器5个频带的归一化能量如图10所示。可以看出，无论对于试件1还是试件2，能量都主要集中在频带2，即100～200 kHz之间。

图10 试件2五个频带归一化能量图(30°断铅)Fig.10 Normalization energy value of the five frequency bands(specimen 1 with 30°angle pencil lead break)

同样以离断铅点最近的第1个传感器的AE信号作为参考，用频带能量相对衰减率描述AE信号在各个频带的衰减特性，第j个传感器第i个频带的能量相对衰减率为

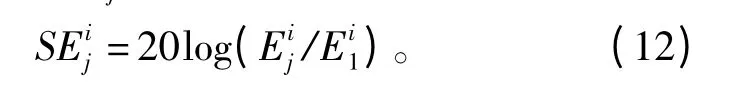
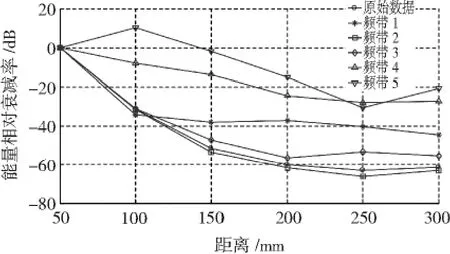
图11 试件1五个频带相对衰减率曲线(30°角断铅)Fig.11 The relative attenuation rate curve of five frequency bands on specimen 1 with 30°angle pencil lead break

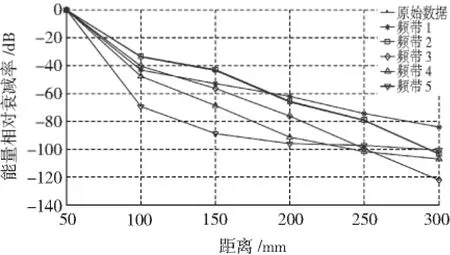
图12 试件2五个频带相对衰减率曲线(30°角断铅)Fig.12 The relative attenuation rate curve of five frequency bands on specimen 2 with 30°angle pencil lead break

图11为试件130°角断铅5个频带和原始数据的相对衰减率曲线，图12为试件2 30°角断铅5个频带和原始数据的相对衰减率曲线。可以看出，无论对于试件1还是试件2，频段2的衰减特性都与原始信号的衰减特性基本一致，说明频带2的信号能准确体现原始信号的衰减特性，因此可以利用频带2信号代替原始信号进行研究。同时，通过图12可以看出，频带越高，衰减越快，这与理论分析也是一致的。

4 结论

本文对直升机动部件常用复合材料试件，碳纤维材料试件和蜂窝材料试件进行了传播特性断铅试验，并且首次利用谐波小波包分析了声发射信号在各个频带上的衰减特性，结果表明:

1)对于本文所用的碳纤维材料试件，在200 mm之后，声发射信号衰减特性偏离理想衰减特性很大，单纯利用时差、能量法进行定位将会存在很大误差，因此需要研究更有效的定位方法。

2)对于本文所用的蜂窝材料试件，频率越高，衰减越快，对于衰减较大的无损检测场合，应该选择较低频率范围提取信号特征。

3)对于本文所研究的两种试件，100～200 kHz频带的衰减特性与原始信号基本一致，可以利用此频带信号代替原始信号进行研究。

[1]NIVESRANGSAN P，STEEL J A，REUBEN R L.AE mapping of engines for spatially located time series [J].Mechanical Systems and Signal Processing，2005，19(5):1034 －1054.

[2]JEONG H.Analysis of plate wave propagation in anisotropic laminates using a wavelet transform[J].NDT＆E International，2001，34(3):185－190.

[3]孙立瑛，李一博，靳世久，等.充液管道中声发射波的传播及衰减特性研究[J].压电与声光.2008，30(4):401－403.SUN Liying，LI Yibo，JIN Shijiu，et al.Study on propagation and attenuation characteristics of acoustic emission wave propagation along fluid loaded pipeline[J].Piezoelectrics ＆ Acoustooptics，2008，30(4):401 －403.

[4]王向红，朱昌明，毛汉领，等.基于声发射技术的水轮机转轮叶片疲劳裂纹扩展速率实验研究[J].中国机械工程，2009，20(7):847－851.WANG Xianghong，ZHU Changming，MAO Hanling，et al.Fatigue crack growth rate of hydraulic turbine blade using acoustic emission technique[J].China Mechanical Engineering，2009，20(7):847－851.

[5]毛汉领，王向红，黄振峰.基于小波包分析的声发射信号界面的衰减研究[J].振动与冲击，2008，27(9):139－141，189.MAO Hanling，WANG Xianghong，HUANG Zhenfeng.Attenuation of acoustic emission signals due to discontinuous interface based on wavelet packet analysis[J].Journal of Vibration and Shock，2008，27(9):139 －141，189.

[6]WANG X H，ZHU C M，MAO H L，et al.Wavelet packet analysis for the propagation of acoustic emission signals across turbine runners[J].NDT＆E International，2009，42(1):42 －46.

[7]张文斌，周晓军，林勇，等.基于谐波小波包方法的旋转机械故障信号提取[J].振动与冲击，2009，28(3):87 －89，97，201.ZHANG Wenbin，ZHOU Xiaojun，LIN Yong，et al.Harmonic wavelet package method used to extract fault signal of a rotation machinery[J].Journal of Vibration and Shock，2009，28(3):87－89，97，201.

[8]李舜酩.谐波小波包方法及其对转子亚频轴心轨迹的提取[J].机械工程学报，2004，40(9):133－137.LI Shunming.Harmonic wavelet packets method and used on accurate obtaining the orbit of rotor sub-frequency signal[J].Chinese Journal of Mechanical Engineering，2004，40(9):133－137.

[9]丁建明，林建辉，杨强，等.基于谐波小波奇异熵的轴承故障实时诊断[J].中国机械工程，2010，21(1):55－58.DING Jianming，LIN Jianhui，YANG Qiang，et al.Real-time diagnosis of bearing faults based on harmonic wavelet singular entropy[J].China Mechanical Engineering，2010，21(1):55 －58.

[10]赵元喜，胥永刚，高立新，等.基于谐波小波包和 BP神经网络的滚动轴承声发射故障模式识别技术[J].振动与冲击，2010，29(10):162 － 165，257.ZHAO Yuanxi，XU Yonggang，GAO Lixin，et al.Fault pattern recognition technique for roller bearing acoustic emission based on harmonic wavelet packet and BP neural network[J].Journal of Vibration and Shock，2010，29(10):162 －165，257.

[11]朱洪俊.非平稳信号瞬时特征提取的谐波小波方法[J].机械工程学报，2008，44(5):191－195.ZHU Hongjun.Extraction of instantaneous characteristics of nonstationary signal using harmonic wavelet transforms[J].Chinese Journal of Mechanical Engineering，2008，44(5):191 －195.

[12]NEWLAND D E.Harmonic wavelet analysis[J].Proc R Soc Land A，1993，443:203－225.

[13]NEWLAND D E.Harmonic wavelet analysis[J].Part 1:Theory Trans ASME J Vibration＆Acoustic，1994，116:409－416.

[14]NEWLAND D E.Harmonic wavelet analysis[J].Part 2:Wavelet map Trans ASME J Vibration＆ Acoustic，1994，116:417－425.