基坑支撑系统的优化分析

2012-01-23胡正威罗晓辉郭陈安

土木工程与管理学报 2012年2期

胡正威，罗晓辉，郭陈安

(华中科技大学土木工程与力学学院，湖北武汉 430074)

基坑工程围护结构设计包含支护系统与支撑系统两方面[1]，在对基坑安全等级、周边环境、地下水条件等相关方面充分分析的基础上，基于围护结构选型理论评估备选模型的整体工作性能，进而确定围护结构的支护系统与支撑系统的有关设计参数[2，3]。然而现实工程设计中由于设计理论与计算方法的原因，使得围护结构支撑系统的布置方式难以满足施工要求[4]，因此需要对选型所确定的围护结构支撑系统优化设计。吴恒[5]基于桩锚围护结构体系的总造价建立优化模型，采用协同演化计算方法实现优化分析的结果；肖专文[6]、刘剑平[7]以围护结构细部设计的材料造价要求建立优化目标函数，采用遗传算法[8]实现优化计算结果的评估。但是基于造价(特别是仅考虑造价这单一因素)的目标函数显然淡化了基坑围护结构设计以安全第一的要求，而且在细部设计优化方面也难以实现[9]。

实际工程中基于施工的要求，对于围护结构支撑系统的优化通常是希望在保证安全标准的同时，随开挖深度设置横撑竖向间距和横撑沿水平向间距越大越好。因此针对支撑系统的优化采用强度与变形安全控制的要求建立优化分析模型。

1 优化分析模型

1.1 一般数学模型

深基坑工程优化设计的一般数学模型表示为[9]：

(1)

式中X=(x1,x2,…,xn)为优化设计参数向量；f(X)为约束函数，通常基于某一优化目标建立，可以显式或隐式表达；gi(X)为等式约束条件，n为等式约束条件数目；yj(X)为不等式约束条件，m为不等式约束条件数目。

约束条件主要有三类：(1)设计变量约束，通常是指变量本身的取值区间，即值域；(2)变量的一致性约束，一般为各种设计变量之间的相互制约关系，包括理论推演、统计推演；(3)设计准则约束，通常是指规范、规程所规定必须满足的条件。

1.2 基于FEM的优化分析模型

对于优化设计的一般数学模型式(1)而言，关键是建立约束函数f(X)。然而对于围护结构的支撑系统而言，约束函数是极为复杂的。采用FEM仿真计算的优化方法，约束函数可采用下式：

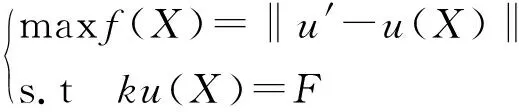
(2)

式中X为设计优化参数向量，u′为基于某种设计准则所要求必须满足的位移阈值，u(X)为基于设计优化参数向量计算的位移值，k、F分别为有限元刚度矩阵及等效节点力，‖·‖为定义在数值空间的某种范数，若采用欧氏范数，即2范数，表示为‖u′-u(X)‖2。

对于深基坑而言设计优化参数向量众多，针对围护结构的支撑系统优化，在变形控制原则下，其优化参数是横撑道数、横撑的水平间距，以及环境安全控制条件。故式(2)的约束条件可表述为：

(1)横撑道数的约束条件：L≤Lv，Lv为横撑道数。因为施加横撑预加力的差异，横撑还可采用钢筋混凝土、钢管等不同形式，故约束条件也可表示为：Lv=Lv1+Lv2，其中Lv1、Lv2分别为钢筋混凝土、钢管的横撑道数；

(2)横撑的水平间距约束条件可表示为H≤Ls，Ls为满足施工要求的横撑水平间距。各层横撑的水平间距也可设置为不同，即H≤Lsi，i=1,2,…,Lv；

(3)环境安全控制约束条件。例如围护结构沿深度的水平位移、周边建筑的位移控制等，可表示为si≤sei(i=1,2,…,t)，其中sei为某一位移阈值。

因为约束函数f(X)取为位移阈值与位移计算值之差的欧氏范数，即计算空间与位移阈值空间的距离，求解式(2)的方法很多，如牛顿法、变度量法[10]，以及免疫进化规划法[11]等。从工程安全角度出发应有欧氏范数越大越好，但是欧氏范数越大势必导致工程成本越大，从这个意义上讲欧氏范数并非越大越好。基于范数非负性，所以有(‖u′-u(X)‖2)min=0。显然，理论上若(‖u′-u(X)‖2)min=0，说明位移计算值均达到了位移阈值，即u′=u(X)。另一方面，当u(X)=0时，说明‖u′-u(X)‖2→(‖u′-u(X)‖2)max。由此可见，‖u′-u(X)‖2→0反映出围护结构是最危险的，当‖u′-u(X)‖2→(‖u′-u(X)‖2)max反映出围护结构是最安全的。而‖u′-u(X)‖2不仅与设计优化参数向量X有关，还取决于环境安全控制约束条件的控制点数量，即t的大小。从优化设计的可靠性而言，理论上t越大越好。考虑到应用欧氏范数尚未见应用于优化分析，因此从实用角度采用类比法进行比较，并采用牛顿法计算‖u′-u(X)‖2。

2 实例应用分析

2.1 工程概况

武汉某地铁三、七号线的交换车站，呈十字形。车站地貌单元类型为长江Ⅰ级阶地，地面高程为20～22 m。基坑场地岩土材料的主要参数见表1。车站地下结构为三层，东西向长260 m，宽约30～60 m，南北向长220 m，宽约30～46 m，主体基坑标准段开挖深度为28.52 m。基坑围护结构为地下连续墙和内支撑结构。地下连续墙厚度1200 mm，地下连续墙插入强风化砂砾岩(15-1)或中风化泥质粉砂岩(15a-2)深度不少于5.0 m。内支撑为八道(最后一道为换撑)，其中标准段分别有混凝土支撑四道、φ609钢管支撑四道。混凝土横撑水平间距为6.0 m，钢管支撑水平间距为3.0 m，设计预加力500 kN。沿基坑东西向的南侧有一外挂站厅结构(上部为市政污水箱涵)，附属基坑拟开挖的基坑宽度14.11 m、深度13.51 m，基坑北侧采用厚度800 mm地下连续墙，墙体深度插入粉细砂(4-1)不少于2.0 m，采用二道φ609钢管支撑。外挂站厅结构地基拟采用竖向增强体加固(如粉喷桩、深层搅拌桩等)，置换率取m=0.5～0.6，加固深度11.0 m。

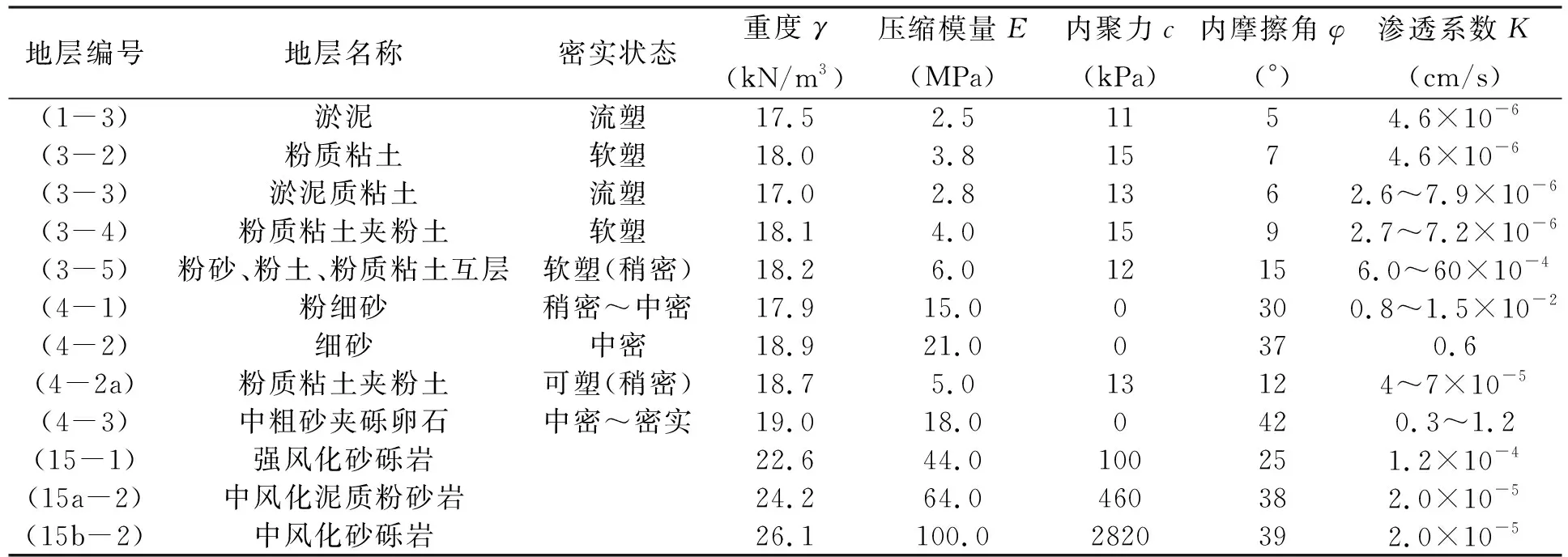
表1 车站基坑地基土厚度与主要物理力学参数

2.2 FEM建模与优化目标

基坑标准段FEM建模如图1。为分析方便，将主体基坑左右地连墙表示为1号、2号墙，外挂站厅、污水箱涵右侧边缘标识为①点与②点。施工顺序为先开挖附属基坑，完成相应的地下结构后回填，恢复路面交通，再实施主体基坑施工。根据施工要求与环境安全控制需要，拟定的支撑系统优化设计目标是：(1)尽可能增大钢管横撑水平间距，以便于施工；(2)去掉换撑；(3)外挂站厅、污水箱涵的水平位移满足结构安全的控制要求。考虑到优化计算的针对性，选择钢换撑水平间距分别为3.0、4.0、5.0 m，优化设计预加力分别为1800～2000 kN。拟定的支撑系统优化方案见表2。

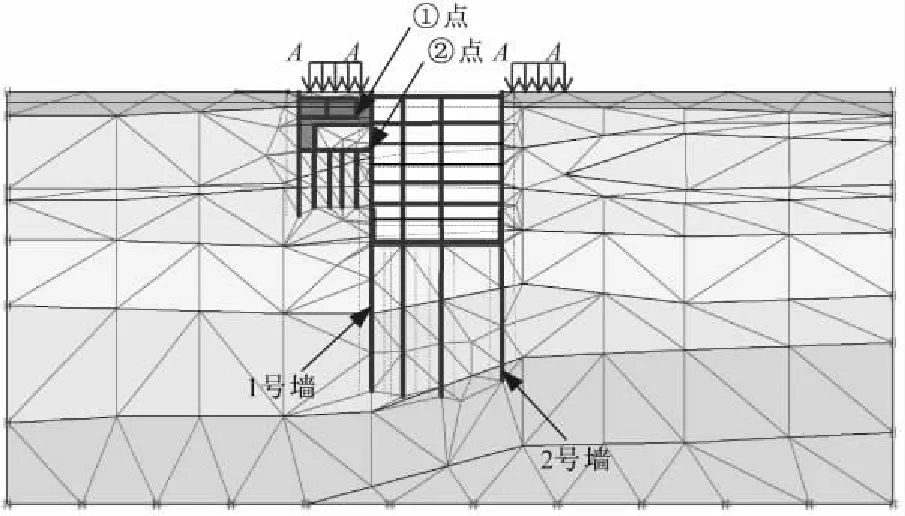
图1 基坑标准段FEM建模

方案一二内容(1)第二道砼横撑下降1.0 m;(2)剔除第三道钢管横撑;(3)第四道钢管横撑上抬1.0 m;(4)第五道砼横撑下降1.0 m(5)剔除换撑(第八道钢管横撑)。(1)第二道砼横撑下降1.0 m;(2)剔除第三道钢管横撑;(3)第四道钢管横撑上抬1.0 m;(4)第五道砼横撑改为钢管横撑;(5)剔除换撑(第八道钢管横撑)。

基于优化目标的要求，相应式(2)的约束条件即可表述为：(1)主体基坑地连墙水平位移不大于0.15%H(H为开挖深度)，且不大于40 mm，墙顶水平位移不大于30 mm；(2)环境地面沉陷不大于0.15%H，即不大于42.78 mm；(3)外挂站厅、污水箱涵的①点与②点水平位移不大于10.0 mm。

2.3 优化分析

图2、3分别展示了原方案与优化方案(钢换撑水平间距为5.0 m)在开挖结束、最后一道横撑拆除时1号、2号地连墙水平位移的比较。由图可见：(1)通常开挖结束时墙体水平位移达到最大值，优化方案二的1号墙最大水平位移减少约12 mm，2号墙最大水平位移减少约18 mm。但最大水平位移深度并没有显著的变化；(2)当最后一道横撑拆除时，优化方案二的1号墙最大水平位移仅增加3 mm，2号墙最大水平位移也只增加了2 mm。这说明支撑系统优化方案二，在开挖结束时既可以保障墙体位移处于安全状态，又可以在最后一道横撑拆除而未施设换撑时保障墙体位移仍处于安全状态。

图4展示了不同内支撑方案时，墙顶水平位移随开挖深度的变化。由图可见：(1)在挖深小于14.0 m时，1号墙墙顶水平位移随挖深的增加而增加，之后则是随挖深增加而减小。而2号墙墙顶水平位移则正好相反，在开挖结束时达到最大。但均未超出规范预警值；(2)就墙顶水平位移而言，2号墙是关键。图中显示在挖深大于14.0 m之后，优化方案二显著较原方案、优化方案一有显著的改善。

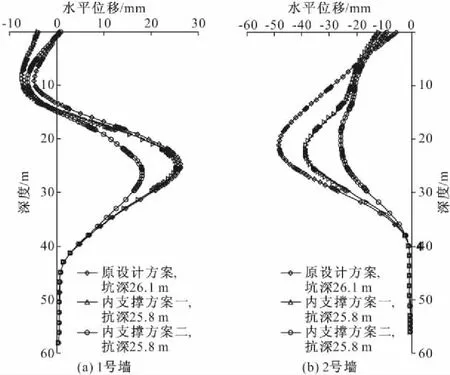
图2 原方案、优化方案的地连墙水平位移比较

图3 拆除最后一道横撑时地连墙水平位移比较

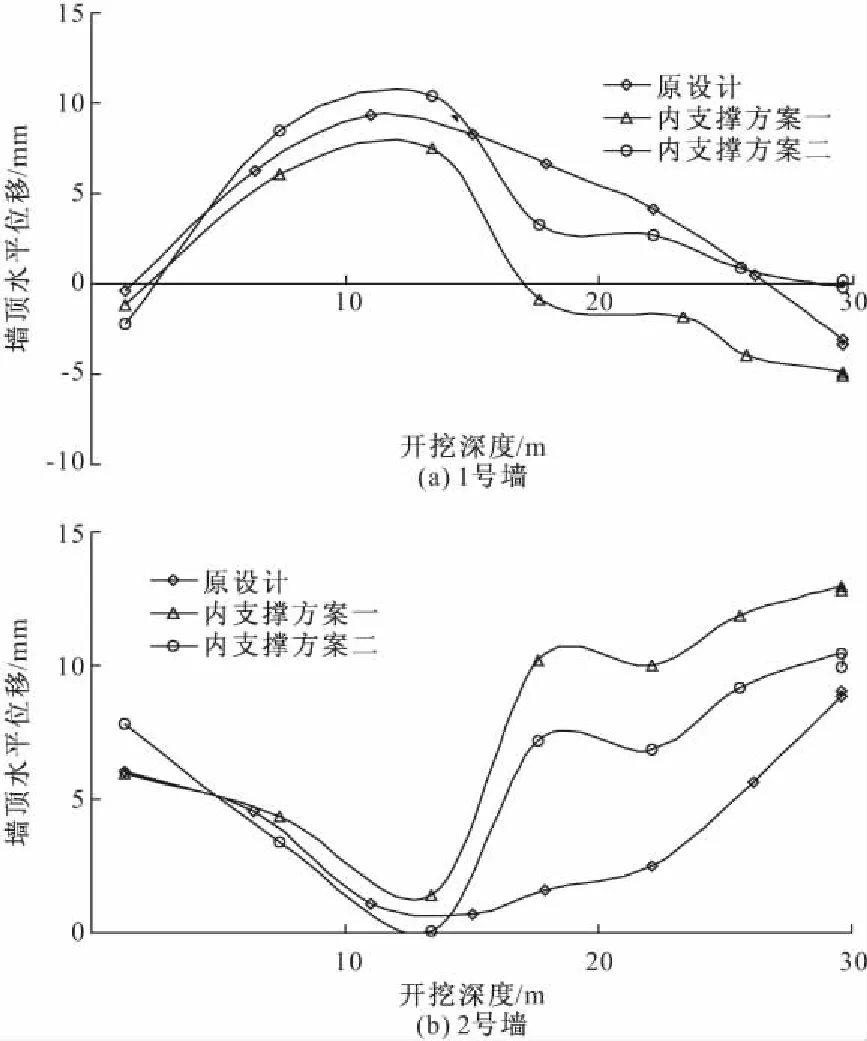
图4 墙顶水平位移比较

图5、6分别展示了开挖深度为26.1 m(25.8 m)和设置地下主体结构底板、并拆除最后第一道支撑后2号墙外地面沉陷的比较。由图可见：(1)优化方案一、二均能较好地控制墙外地面沉陷满足小于42.78 mm的要求，而原设计方案所产生的墙外地面沉陷远超出设计要求；(2)就墙外地面沉陷的影响范围和最大沉陷中心位置比较而言，优化方案二优于优化方案一，而优化方案一优于原设计方案。

图5 开挖结束时地面沉陷的比较

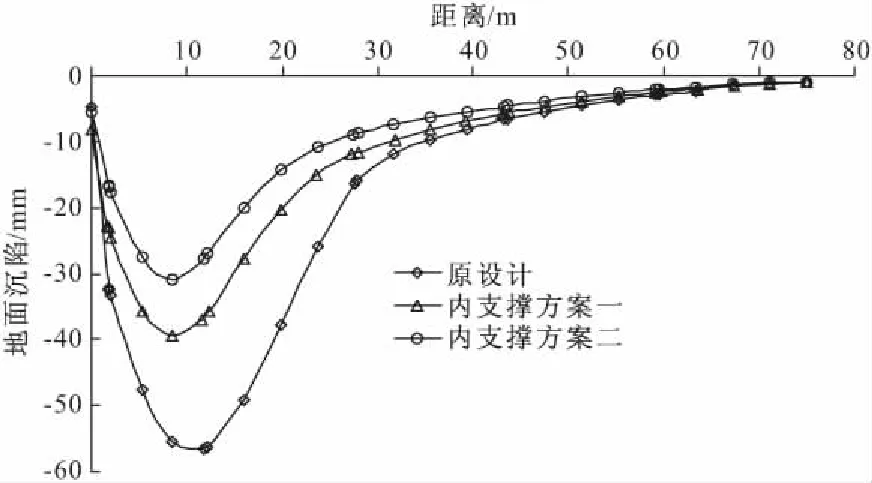
图6 拆除最后一道横撑时地面沉陷的比较

钢管横撑间距大小直接影响到墙体水平位移的发展。图7分别展示了三种方案，当钢管横撑轴心间距分别取3.0 m、4.0 m和5.0 m时，墙体最大水平位移随开挖深度的变化。其基本规律由图可见：(1)不论何种横撑设置方案，横撑轴心间距越大使得在同一开挖深度时最大水平位移就越大；(2)横撑轴心间距越大，当拆除最后一道横撑(原方案为第7道钢管横撑，内支撑方案一、二分别为第6道钢管横撑)，但尚未施加换撑时最大水平位移的增加量也随之增大；(3)就三种方案比较而言，显然优化方案二为最佳，当横撑轴心间距为5.0 m时，最大水平位移尚未超过水平位移预警值，且拆除第6道钢管横撑条件下，最大水平位移仅增加1.8 mm。

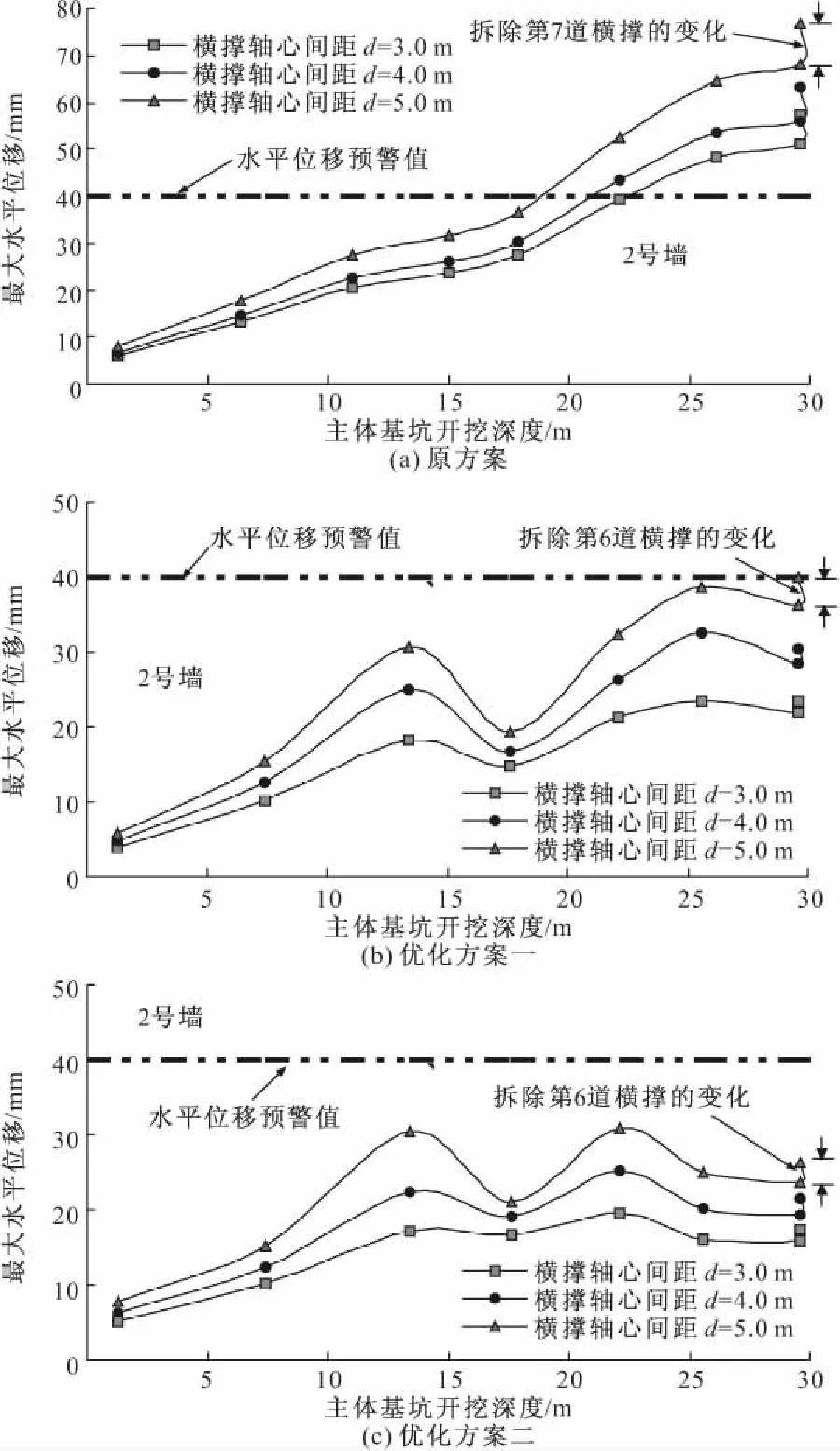
图7 横撑轴心距对最大水平位移的影响

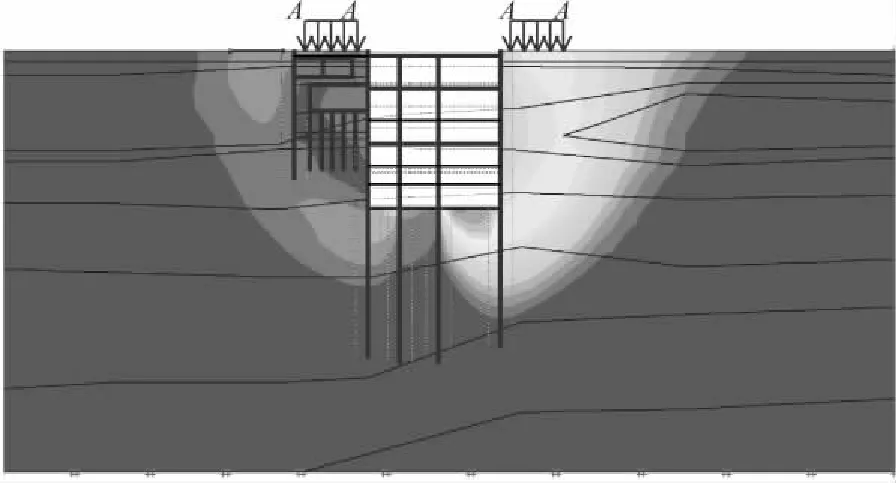
图8 基坑整体稳定状态

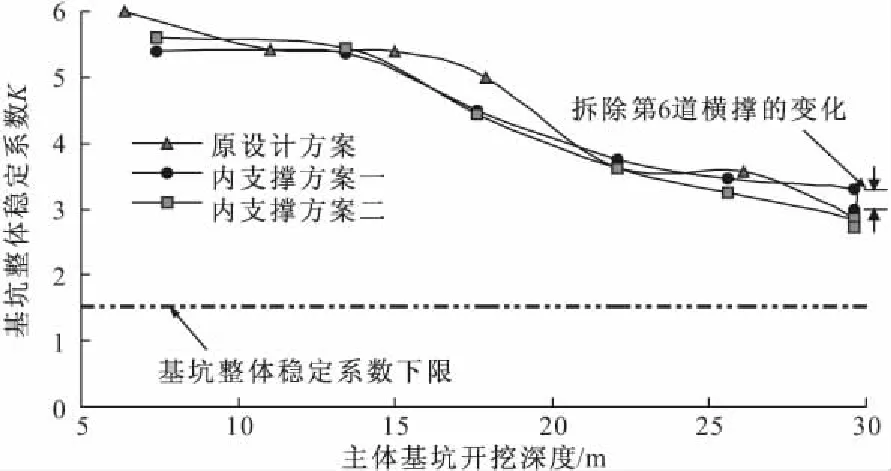
图9 基坑整体稳定系数随开挖深度的变化

围护结构整体稳定系数是基坑开挖进程中描述其整体安全状态的主要指标，整体稳定性采用强度折减法计算。图8展示了采用优化方案二、开挖结束时的基坑稳定状态，图9给出了三种支撑方案整体稳定系数随开挖深度的变化。由图可见：(1)采用优化方案一、二，在各开挖深度时其整体稳定系数略低于原设计方案0.3左右；(2)最后一道横撑拆除时，整体稳定系数均降低约0.2～0.4；(3)就主体基坑1、2号墙而言，其整体稳定主要取决于2号墙，因此2号墙应是施工监测的重点；(4)三种内支撑方案的整体稳定系数在不同的开挖深度条件下，均大于规范所要求的整体稳定系数1.5。

图10 欧氏范数随开挖深度的变化

图10展示了优化方案二的欧氏范数随开挖深度的变化。由图可见，横撑的水平间距对欧氏范数的影响是显著的，开挖深度小于12.0m时，横撑水平间距对欧氏范数影响不大，但是当开挖深度大于15.0 m之后水平间距d=3.0 m时，欧氏范数近似呈直线减小。当d=5.0 m时，欧氏范数随开挖深度近乎呈抛物线减小，但达到设计开挖深度时欧氏范数则逐渐趋于稳定，这也就意味着围护结构系统的整体位移状态趋向于稳定，且(‖u′-u(X)‖2)min=1.313>0。由此说明采用钢横撑水平间距5.0 m时，基坑整体开挖过程是安全的。