2－度量空间上具有唯一公共不动点的映射族的收缩型条件

严今石，朴勇杰，崔海兰

（1.延边教育出版社，吉林 延吉133000；2.延边大学理学院 数学系，吉林 延吉133002；3.吉林市朝鲜族中学，吉林132021）

2－度量空间上具有唯一公共不动点的映射族的收缩型条件

严今石1，朴勇杰2＊，崔海兰3

（1.延边教育出版社，吉林 延吉133000；2.延边大学理学院 数学系，吉林 延吉133002；3.吉林市朝鲜族中学，吉林132021）

利用新的收缩型条件，给出了完备的2－度量空间（X，d）上的自映射族｛Ti｝i∈N具有唯一公共不动点的定理.该结果推广和改进了很多2－度量空间上的收缩型映射族的唯一公共不动点定理.

2－度量空间；柯西序列；收缩条件；公共不动点

有关在2－度量空间上的自映射族具有唯一公共不动点的定理已有许多报道［1－7］，其中大部分所得结论都是在非常弱的收缩型或拟收缩型假设下得到的，而且没有附加映射族满足交换律、序列连续及在某一点一致有界［3］等条件，这些结果推广和改进了很多相关的结果.本文将引进一种新的收缩型条件，并给出当自映射族满足一定条件时具有唯一公共不动点的定理，以进一步推广和完善公共不动点理论.

1 基本概念

定义1 2－度量空间（X，d）是指1个集合和1个映射d∶X×X×X→［0，＋∞）满足下列条件：① 对X中2个不同的元x，y，存在u∈X使得d（x，y，u）≠0；② 当x，y，z中至少有2个相等时，d（x，y，z）＝0；③d（x，y，z）＝d（u，v，w），其中｛u，v，w｝是｛x，y，z｝的1个排列；④d（x，y，z）≤d（x，y，u）＋d（x，u，z）＋d（u，y，z），对任何x，y，z，u∈X.

定义2 2－度量空间X的1个序列｛xn｝为柯西序列是指对任何ε＞0，存在正整数N使得n，m＞N时，d（xn，xm，a）＜ε；即limn，m→＋∞d（xn，xm，a）＝0，对任何a∈X.

定义3 序列｛xn｝收敛于x∈X是指对任何ε＞0，存在正整数N使得n＞N时，d（xn，x，a）＜ε；即limn→＋∞d（xn，x，a）＝0，对任何a∈X，并简记为xn→x.

定义4 1个2－度量空间X被称为完备的是指X中的每1个柯西序列都收敛.

下列引理可在文献［4－7］中查到.

引理1 如果｛xn｝是2－度量空间的1个序列，并且存在h∈ ［0，1）满足d（xn＋1，xn，a）≤hd（xn，xn－1，a），对任何a∈X和n＝1，2，…，则d（xn，xm，xl）＝0，对所有n，m，l∈N，且｛xn｝是柯西序列.

引理2 如果｛xn｝是2－度量空间中收敛于x的1个序列，则limn→＋∞d（xn，b，c）＝d（x，b，c），对任何b，c∈X.

2 定理及其证明

定理1 设（X，d）是完备的2－度量空间，｛Ti｝i∈N是X上的自映射族.如果存在使得对任何x，y，a∈X成立

其中ui，j（x，y，a）∈ ｛d（x，Tix，a），d（y，Tjy，a），d（x，Tjy，a），d（Tix，y，a），d（x，y，a）｝，则 自 映 射 族｛Ti｝i∈N在X中有唯一的公共不动点.

证明 任意选定x0∈X，并定义xn＋1＝Tn＋1xn，则可得到1个序列｛xn｝n∈N.对任何n∈N及a∈X，根据（1）式有

其 中un，n＋1（xn－1，xn，a） ∈ ｛d（xn－1，Tnxn－1，a），d（xn，Tn＋1xn，a），d（xn－1，Tn＋1xn，a），d（Tnxn－1，xn，a），d（xn－1，xn，a）｝.当un，n＋1（xn－1，xn，a）＝d（xn－1，Tnxn－1，a）＝d（xn－1，xn，a）时，（2）式变成d（xn，xn＋1，a）≤kd（xn－1，xn，a）.当un，n＋1（xn－1，xn，a）＝d（xn，Tn＋1xn，a）＝d（xn，xn＋1，a）时，（2）式变成d（xn，xn＋1，a）≤kd（xn，xn＋1，a）.因此，由k＜1可 知，d（xn，xn＋1，a）＝0 ≤kd（xn－1，xn，a）.当un，n＋1（xn－1，xn，a）＝d（x，Tx，a）＝d（x，x，a）时，由（2）式和条件 ④ 得

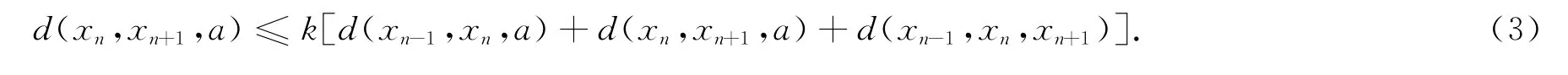
由于d（xn－1，xn，xn＋1）＝d（Tnxn－1，Tn＋1xn，xn－1）≤kun，n＋1（xn－1，xn，xn－1），其中un，n＋1（xn－1，xn，xn－1）∈｛d（xn－1，Tnxn－1，xn－1），d（xn，Tn＋1xn，xn－1），d（xn－1，Tn＋1xn，xn－1），d（Tnxn－1，xn，xn－1），d（xn－1，xn，xn－1）｝＝｛d（xn－1，xn，xn＋1），0｝，因此由k＜1可推出，d（xn－1，xn，xn＋1）＝0.于是（3）式变成d（xn，xn＋1，a）≤k［d（xn－1，xn，a）＋d（xn，xn＋1，a）］，并得到d（xn，xn＋1，a）≤k1－kd（xn－1，xn，a）.当un，n＋1（xn－1，xn，a）＝d（Tnxn－1，xn，a）＝d（xn，xn，a）＝ 0 时，（2）式 显 然 变 成d（xn，xn＋1，a）＝ 0 ≤kd（xn－1，xn，a）.当un，n＋1（xn－1，xn，a）＝d（xn－1，xn，a）时，（2）式变成d（xn，xn＋1，a）≤kd（xn－1，xn，a）.综合上述结果可得

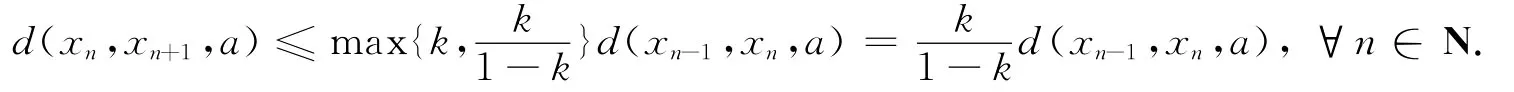
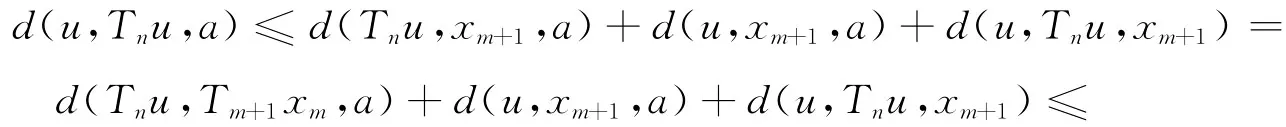
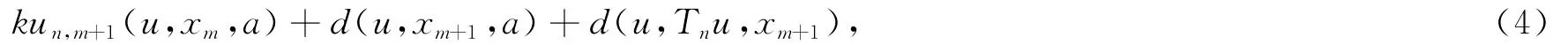
其中un，m＋1（u，xm，a）∈｛d（u，Tnu，a），d（xm，Tm＋1xm，a），d（u，Tm＋1xm，a），d（Tnu，xm，a），d（u，xm，a）｝＝｛d（u，Tnu，a），d（xm，xm＋1，a），d（u，xm＋1，a），d（Tnu，xm，a），d（u，xm，a）｝.当un，m＋1（u，xm，a）＝d（u，Tnu，a）时，（4）式变成d（u，Tnu，a）≤kd（u，Tnu，a）＋d（u，xm＋1，a）＋d（u，Tnu，xm＋1）.令m→＋∞，则由引理2和条件 ② 可得d（u，Tnu，a）≤kd（u，Tnu，a）.于是由k＜1可得d（u，Tnu，a）＝0.当un，m＋1（u，xm，a）＝d（xm，xm＋1，a）时，（4）式变成d（u，Tnu，a）≤kd（xm，xm＋1，a）＋d（u，xm＋1，a）＋d（u，Tnu，xm＋1）.令m→＋∞，则由引理2、柯西条件和条件 ② 可得d（u，Tnu，a）＝0.当un，m＋1（u，xm，a）＝d（u，xm＋1，a）时，（4）式变成d（u，Tnu，a）≤kd（u，xm＋1，a）＋d（u，xm＋1，a）＋d（u，Tnu，xm＋1）.令m→＋ ∞，则由引理2和条件② 可得d（u，Tnu，a）＝0.当un，m＋1（u，xm，a）＝d（Tnu，xm，a）时，（4）式变成d（u，Tnu，a）≤kd（Tnu，xm，a）＋d（u，xm＋1，a）＋d（u，Tnu，xm＋1）.令m→＋∞，则由引理2和条件 ② 可得d（u，Tnu，a）≤kd（u，Tnu，a），于是由k＜1得d（u，Tnu，a）＝0.当un，m＋1（u，xm，a）＝d（u，xm，a）时，（4）式变成d（u，Tnu，a）≤kd（u，xm，a）＋d（u，xm＋1，a）＋d（u，Tnu，xm＋1）.令m→＋∞，则由引理2和条件 ② 可得d（u，Tnu，a）＝0.

综合以上结果，得到d（u，Tnu，a）＝0，∀n∈N.于是Tnu＝u，∀n∈N，即证明了u是｛Ti｝n∈N的公共不动点.

如果v∈X也是｛T｝n∈N的公共不动点，由于u＝T1u，v＝T2v，因此根据条件（1）得到对任何a∈X有d（u，v，a）＝d（T1u，T2v，a）≤ku1，2（u，v，a），其中u1，2（u，v，a）＝ ｛d（u，T1u，a），d（v，T2v，a），d（u，T2v，a），d（T1u，v，a），d（u，v，a）｝＝ ｛0，d（u，v，a）｝.因此由k＜1可推出d（u，v，a）＝0，∀a∈X，于是u＝v，即证明了u是｛Ti｝n∈N的唯一公共不动点.

注记 本定理中采用的收缩型条件不同于本文参考文献及相关论文中给出的收缩型条件.文献中的条件主要采用了线性组合形式的收缩型条件，或用某种多元函数限制的收缩型条件，因此可以说本文利用新的收缩型条件得到的2－度量空间上的公共不动点定理，是对公共不动点理论的进一步推广和发展.

［1］Singh S L.Contractive type principles on 2－metric spaces and applications［J］.Math Sem Notes，1979，7：1－11.

［2］朴勇杰.2－度量空间上收缩型非交换自映射族的唯一公共不动点定理［J］.延边大学学报：自然科学版，2006，32（1）：5－7.

［3］Yang Hansheng，Xiong Dasheng.A common fixed point theorem onp－metric spaces［J］.Yunnan Normal Univ：Natural Sci，2001，21（1）：9－12.

［4］朴勇杰.2－度量空间上具有唯一公共不动点的拟收缩型非交换自映射族［J］.黑龙江大学学报：自然科学版，2006，23（5）：655－657.

［5］Piao Yongjie.Unique common fixed point of a family of self－maps with same type contractive condition in 2－metric space［J］.Anal Theo Appl，2008，24（4）：316－320.

［6］朴勇杰.2－度量空间上具有相同拟收缩型条件的自映射族的唯一公共不动点定理［J］.南京大学学报：数学半年刊，2010，27（1）：82－87.

［7］Piao Yongjie.Uniqueness of common fixed points for a family of mappings withφ－contractive condition in 2－metric spaces［J］.Applied Mathematics，2012，3（1）：73－77.

A contractive condition of mappings having an unique common fixed point on 2－metric spaces

YAN Jin－shi1，PIAO Yong－jie2＊，CUI Hai－lan3
（1.YanbianEducationPublishingCompany，Yanji133000，China；2.DepartmentofMathematics，Collegeof
Science，YanbianUniversity，Yanji133002，China；3.JilinKoreanNationalityMiddleSchool，Jilin132021，China）

A ne wcontractive condition is considered，and an unique common fixed point theorem for self－mappings｛Ti｝i∈Non a 2－metric space（X，d）is given.The result generalizes and improves many unique common fixed point theorem for mappings with contractive conditions on 2－metric spaces.

2－metric space；Cauchy sequence；contractive condition；unique common fixed point

O189.11

A

1004－4353（2012）01－0017－03

2012－02－27＊通信作者：朴勇杰（1962—），男，理学博士，教授，研究方向为非线性分析.

吉林省教育厅“十二五”科学技术研究项目（吉教科字号第2011［434］）