电压型CPT系统输出品质与频率稳定性分析
2012-01-14周诗杰孙跃戴欣唐春森
周诗杰, 孙跃, 戴欣, 唐春森
(重庆大学自动化学院,重庆400030)
0 引言
基于电磁耦合原理的非接触电能传输技术(contactless power transfer,CPT)增加了用电设备的灵活性,弥补了传统接触式电能传输方式存在的器件磨损、碳积以及电火花等缺陷[1-2],是一种安全、可靠、灵活的电能接入新技术[3-4]。为了提高系统的功率容量,CPT系统常通过在能量发射端(原边)和能量接收端(拾取端)串联或者并联电容的方式补偿系统的无功功率,使原边和拾取端均工作在谐振状态。根据补偿电容位置的不同可分为4种基本拓扑,但是目前对各种拓扑的应用场合尚无定论;另一方面,由于采用谐振的方式传输能量,频率的变化会对CPT系统的输出品质造成很大的影响[5],尤其对于拾取端目前对频率漂移仍缺乏有效的控制手段。针对以上问题,文献[6]分析了CPT系统4种不同拓扑输出电压电流的增益,但是并没有总结不同拓扑的适用场合;文献[7]提出了以品质因数来量度拾取端的频率稳定性,并给出了在Qs=2~6时系统工作在最佳状态的结论,但是并没有相关的证明,也未说明这个结论适用于何种拓扑;文献[8]和文献[9]提出了采用动态调谐的方式改变拾取线圈的感值或补偿电容的容值,但是该方法只适用于小功率系统,无法在大功率场合适用。
针对以上问题,本文在对电压型CPT系统工作原理的分析基础上,根据系统原副边的耦合关系建立了系统拾取端的阻抗模型,分别总结了在谐振条件下系统的输出特性和在失谐条件下系统的拾取端阻抗随频率变化的规律。在此基础上,根据对拾取端阻抗的分析,提出了对于电压型CPT系统来说较小的拾取端线圈电感值有益于系统的频率稳定;发现并证明了SP型CPT系统的拾取端至少存在2个谐振频率点和1个负载突变频率点,最后根据3个特殊频率点的关系给出了拾取端电感的取值范围,对实际系统参数设计具有指导意义。为便于分析,本文的一切结论基于以下3条假设:1)忽略系统的内阻损耗和开关损耗;2)电磁转换效率为100%;3)系统输入电压恒定。
1 谐振条件下电压型CPT系统输出分析
为了提高CPT系统的能量传输能力与效率,通常要对系统的原边与拾取端分别串联或者并联电容以补偿系统的无功功率[10]。按照补偿电容位置的不同CPT系统可分为:SS(原边串联补偿电容,副边串联补偿电容)、SP(原边串联补偿电容,副边并联补偿电容)、PS(原边并联补偿电容,副边串联补偿电容)、PP(原边并联补偿电容,副边并联补偿电容)4种基本拓扑结构[11]。其中SS与SP结构属于电压型CPT系统[12],结构如图1所示。
如图1所示,Lp、Cp分别为原边的能量发射线圈和补偿电容,Ls为拾取端的能量接收线圈。M为线圈Lp与Ls的互感;Cs为拾取端的补偿电容,Uin为逆变器输出电压,Uout为系统是输出电压,RL为系统的等效负载。根据互感的性质,当系统拾取端工作在谐振状态时,其反射到原边的阻抗为

式中:Zr为拾取端到原边的反射阻抗;ω为系统工作角频率;Zf为拾取端阻抗。

图1 电压型CPT系统结构简图Fig.1 Voltage type CPT system structure chart
当系统工作在谐振状态时,根据能量守恒定律,可得
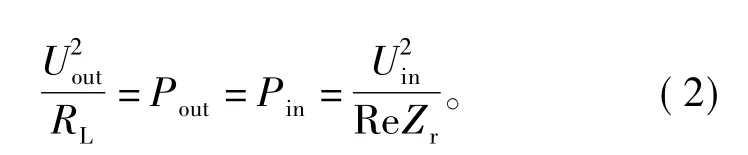
其中:Pin和Pout分别为系统的输入和输出功率;将式(1)带入式(2)化简可得

其中:Is为拾取端输出电流;在谐振的条件下,ω、M和Ls均为定值。由式(3)可知,SS型的CPT系统输出品质与原副边线圈电感值无关,且输出电流恒定,适用于需要恒流输出的场合。SP型CPT系统输出品质与拾取端线圈电感值有关,且输出电压恒定,适用于需要恒压输出的场合。
2 失谐条件下电压型CPT系统输出分析
由于测量,温度,负载性质等诸多客观原因,CPT系统的原边和副边很难全部准确的工作在谐振频率点上,由此造成拾取端阻抗随频率的漂移而波动。为解决系统频率漂移对系统输出品质和效率造成的影响,软开关等浮频控制策略被广泛的应用到CPT系统中。但是浮频控制只是单纯的使系统原边谐振工作在谐振状态,而对于需要大功率输出的系统拾取端来说,由于目前缺乏有效的频率控制策略,只能通过参数设计的手段降低系统输出品质对频率的敏感性。
定义X为拾取端由于频率漂移而产生的阻抗,将X带入式(1)和式(3)中,即可得到电压型CPT系统原边谐振条件下输入输出的电压关系为

在一定的通频范围内,X的值越小,频率对系统输出品质的影响也就越小。根据系统拾取端的阻抗关系,可得X在SS型和SP型系统中的计算公式为

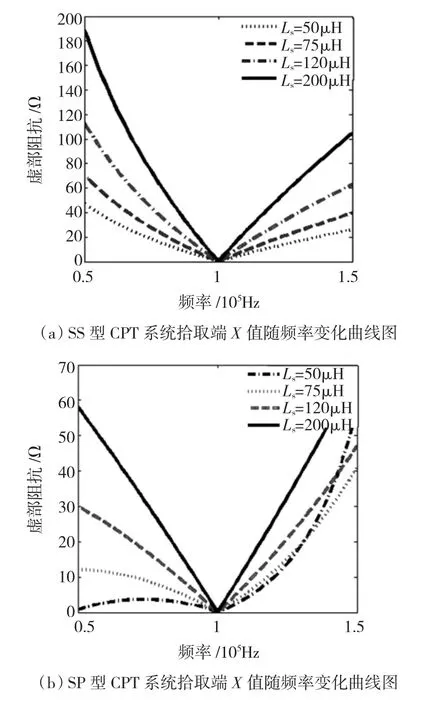
图2 CPT系统拾取端X值随频率变化曲线Fig.2 X changed with frequency in CPT system
图3中f=100 kHz为目标谐振频率。从图3和式(5)中可以看出,对于SS型系统来说,无论负载如何变化,Ls越小,系统虚部阻抗随频率变化就越小,且在目标频率点右侧虚部阻抗随频率的变化率明显小于目标频率点左侧;对于SP型系统来说,在负载一定的情况下,Ls越小,系统虚部阻抗随频率变化就越小,且在目标谐振频率点左侧虚部阻抗随频率的变化率明显小于目标谐振频率点右侧。但是当Ls过小时,拾取端在临近目标频率点左侧会出现第2个谐振频率点,在目标频率点右侧出现1个负载突变频率点,两者之间的距离与负载和拾取端电感值有关,如图4所示。

图3 SP型CPT频率点示意图Fig.3 frequency in different Lsin SP CPT system
SP型CPT系统拾取端负载突变频率点的计算公式为
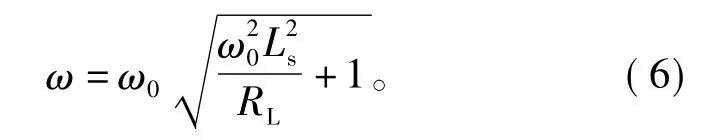
由式(6)可以看出,SP型CPT系统的负载突变频率点与负载和拾取端线圈电感值均有关,将式(6)代入式(3)和式(5)中,得到SP型CPT系统拾取端电感的范围为
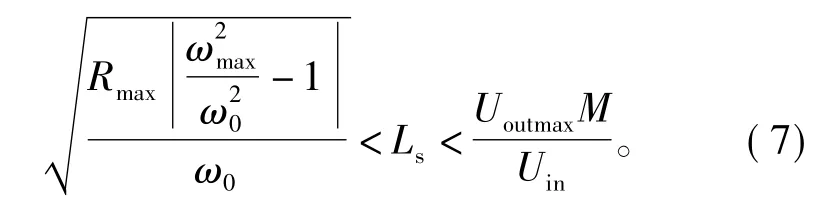
其中:Rmax为系统的最低带载;ωmax为系统可允许的最大工作角频率;Uoutmax为系统允许输出的最大电压值。在设计SP型系统参数时,拾取端线圈电感值必须满足式(7),否则当系统可能会因负载变化工作在负载突变频率点附近,导致系统输出品质变差。
通过以上分析可知:对于SS型CPT系统来说,在保证传输功率和效率的前提下,拾取端电感值应尽量小,当无法保证拾取端谐振时,应尽量使系统工作在略大于目标谐振频率的频率点上;对于SP型CPT系统来说,在保证系统输出品质与稳定性的前提下,拾取端电感值应在系统允许的范围内尽量小,当无法保证拾取端谐振时,应使系统的工作在略小于目标谐振频率的频率点上,并使拾取端电感值满足式(7)。在同样负载条件下,SP系统较SS系统更能够适应频率的变化。
3 实验结果与分析
搭建SP型CPT系统实验平台对上述理论进行验证。电路图如图4所示。

图4 实验装置电路图Fig.4 circuit diagarm of experiment device
图 4 中 Lp=440 μH;Cp=0.157 μF;Ls=60 μH;Cs=1.05 μF;M=46.3 μH;Vin=60 V;系统的谐振频率为f=20 kHz。由S1-S4构成的全桥逆变器始终工作在软开关状态。拾取端并联可调电容矩阵,调节系统的工作频率。
图5为SP型CPT系统在谐振状态下恒压输出实验。当系统稳定工作在谐振状态时,在某一时刻切换负载,系统输出电压基本未改变,输出电流减小,输出功率降低。由图5可知,在谐振条件下SP型CPT系统输出具有恒压特性。
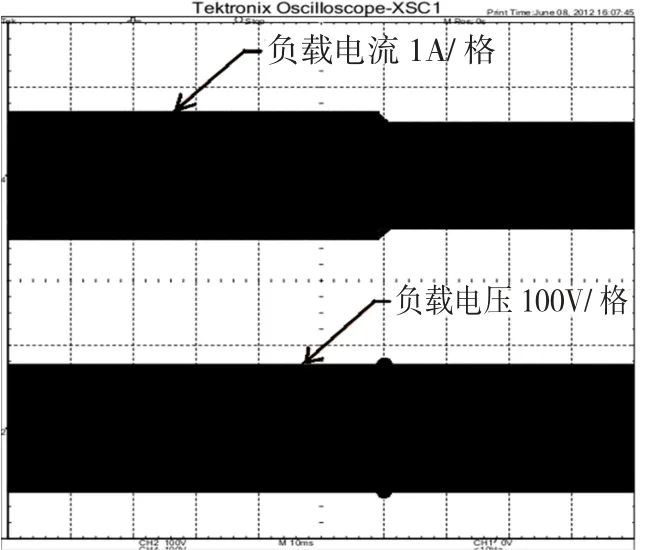
图5 SP型系统谐振条件下恒压输出波形图Fig.5 Constant voltage output for SP CPT system in resonance
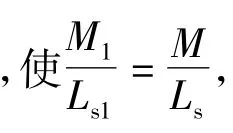
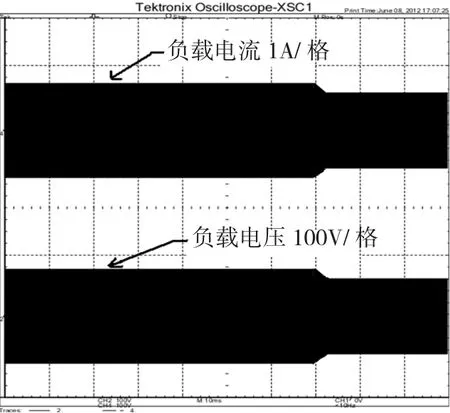
图6 拾取线圈为Ls的系统输出电压电流波形图Fig.6 Voltage and current waveforms of Ls’s system
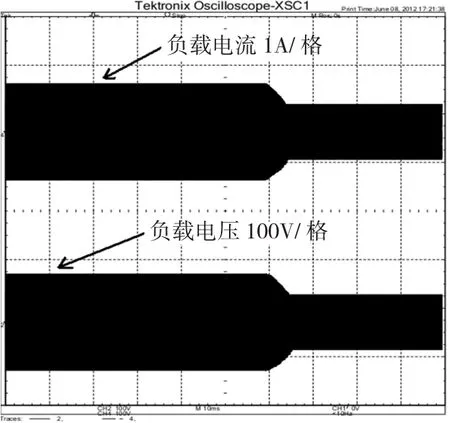
图7 拾取线圈为Ls1的系统输出电压电流波形图Fig.7 Voltage and current waveforms of Ls1’s system
由图6可知,当系统的工作频率由谐振频率(20 kHz)漂移至18 kHz后,拾取端电感值较小的系统输出功率由谐振时的50 W降至40 W;拾取端电感值较大的系统输出功率由50 W降至15 W左右。可以看出,拾取端电感值较小的系统的频率鲁棒性明显高于拾取端电感值较大的系统。
4 结语
通过对电压型CPT系统拾取端在谐振条件下系统输出品质和失谐条件下频率-阻抗模型变化规律的分析,总结出SS型系统适用于恒流输出的场合,SP型系统适用于恒压输出的场合;当无法保证系统谐振时,对于电压型CPT系统来说,较小的拾取端电感值可以提高系统的频率稳定性;与SS型系统不同,SP型系统至少存在两个谐振点和一个负载突变频率点,并给出了SP型系统拾取端电感的取值范围;SP型系统比SS型系统在同样的频率漂移影响下具有更好的鲁棒性。
[1] BOYS J T,GREEN A W.Inductively coupled power transmissionconcept design and application[J].IPENZ Trans,1995,22(1):1-9.
[2] GREEN A W,BOYS J T.10kHz inductively coupled power transfer-concept and control[C]//Proceedings of the 5th International Conference on Power Electronics and Variable Speed Drives.London: [s.n.],1994:694 -699.
[3] 武瑛,严陆光,徐善刚.新型无接触电能传输系统的稳定性分析[J].中国电机工程学报,2004,24(5):63-66.WU Ying,YAN Luguang,XU Shangang.Stability analysis of the new contactless power delivery system[J].Proceedings of the CSEE,2004,24(5):63 -66.
[4] 王璐,陈敏,徐德鸿.磁浮列车非接触紧急供电系统的工程化设计[J].中国电机工程学报,2007,27(18):67-70.WANG Lu,CHEN Min,XU Dehong.The engineering design of contactless emergency power supply in maglev[J].Proceedings of the CSEE,2007,27(18):67 -70.
[5] 王金平,许建平,兰燕妮.开关变换器双频率控制技术[J].电机与控制学报,2010,14(12):9-14.WANG Jinping,XU Jianping,LAN Yanni.Bi-frequency control technique for switching converters.[J].Electric Machines and Control,2010,14(12):9 -14.
[6] 周雯琪,马皓,何湘宁.感应耦合电能传输系统不同补偿拓扑的研究[J].电工技术学报,2009,24(1):133-139.ZHOU Wenqi,MA Hao,HE Xiangning.Investigation on different compensation topologies in inductively coupled power transfer system[J].Transactions of China Electrotechnical Society,2009,24(1):133-139.
[7] STIELAU O H,COVIC G A.Design of loosely coupled inductive power transfer systems[C]//International Conference on Power System Technology,2000.
[8] HSU J U W,HU A P.Determining the variable inductance range for an LCL wireless power pick-up[C]//IEEE Conference on E-lectron Devices and Solid-State Circuits,2007,EDSSC.
[9] 孙跃,王智慧,戴欣,等.非接触电能传输系统的频率稳定性研究[J].电工技术学报,2005,20(11):56-59.SUN Yue,WANG Zhihui,SU Yugang,et al.Study of frequency stability of contactless power transmission system[J].Transactions of China Electrotechnical Society,2005,20(11):56 -59.
[10] 张治国,谢运祥,袁兆梅,等.一种高频LCC谐振变换器的近似分析方法[J].电机与控制学报,2011,15(7):44-49.ZHANG Zhiguo,XIE Yunxiang,YUAN Zhaomei,et al.Novel proximate analysis method of LCC resonant converter for high frequency applications[J].Electric Machines and Control,2011,15(7):44-49.
[11] 孙跃,夏晨阳,苏玉刚,等.导轨式非接触电能传输系统功率和效率的分析与优化[J].华南理工大学学报,2010,38(10):123-129.SUN Yue,XIA Chenyang,SU Yugang,et al.Analysis and optimization of transmission power and efficiency for rail-type contactless power transfer system[J].Journal of South China University of Technology,2010,38(10):123 -129.
[12] 杨民生,王耀南.感应耦合电能传输系统动态解谐传输功率控制[J].电机与控制学报,2012,16(1):72-78.YANG Minsheng,WANG Yaonan.Transferred power regulating method with a dynamically detuning inductor for ICPT pick-ups.[J].Electric Machines and Control,2012,16(1):72 -78.
