基于空间矢量调制的直接转矩控制算法研究

张华强， 王新生， 魏鹏飞， 徐殿国

(哈尔滨工业大学电气工程系，黑龙江哈尔滨150001)

0 引言

由于交流异步电机具有结构简单、无换向器、坚固耐用及成本低廉等优点，交流调速系统得到广泛应用。为了改进感应电机的控制性能，自20世纪70年代矢量控制(vector control，VC)问世以来，新型感应电机控制方案不断更新，如直接转矩控制(direct torque control，DTC)，反馈线性控制(feedback linearization control，FLC)等，使得感应电机控制性能可与直流电机相媲美［1］。其中由于DTC控制方案具有控制结构简单，对参数变化鲁棒性强，转矩动态响应快等优点得到研究人员的广泛关注。

传统DTC控制方案使用两个滞环比较器来控制电机定子磁链和转矩，可以快速控制磁链和转矩，使误差稳定在滞环宽度内。由于滞环控制器自身的原因，逆变器开关频率不恒定，导致转矩脉动不可避免。为解决传统DTC方案中转矩脉动大，开关频率不固定等问题，很多改进的DTC控制方案应运而生，如改进的直接转矩控制方案［2－3］、无差拍直接转矩控制方案、基于磁链转矩预测控制和离散空间矢量调制(discontinues space vector modulation，DSVM)的直接转矩控制方案［4］和模糊神经网络直接转矩控制方案［5］等。本文提出一种基于空间矢量调制的直接转矩控制方案(direct torque control with space vector modulation，DTC －SVM)，以磁链和转矩为控制量，获得矢量控制连续平滑和DTC快速响应性能。

1 传统DTC控制方案

传统DTC方案是通过查表方式选择合适的电压矢量，来实现磁链和转矩的直接控制［6］，使其限定在一定误差范围内。传统DTC控制方案原理如图1所示。

图1 传统DTC控制原理Fig．1 The control theory diagram of traditional DTC

传统DTC控制方案是基于感应电机在两相静止坐标α－β上的模型建立的。先测量电机端电压和电流，通过三相静止坐标到两相静止坐标变换3s/2s，转换到两相静止坐标系。然后根据电机模型中的方程来计算定子磁链和电磁转矩，并计算出磁链所在的扇区。将给定的磁链和转矩分别与计算得到的磁链和转矩相比较，产生的误差由滞环比较器控制，误差符号连同磁链所在扇区的信号，便可以选择相应的电压空间矢量，来控制磁链和转矩的误差在滞环宽度内。感应电机电磁转矩方程为

式中:ms为电源相数;Pb为电机极对数;Ls、Lr和Lm分别为电机定子、转子电感和互感;ψs、ψr分别为定子、转子磁链幅值;γ为定子磁链与转子磁链的夹角。

考虑到转子磁链和定子磁链的幅值保持不变，可以通过改变定、转子磁链的相对夹角来改变电磁转矩。而在感应电机中转子磁链相对于定子磁链来说变化缓慢，可认为其相对定子磁链静止。那么，只能改变定子磁链来使二者相对夹角改变。定子磁链由定子电压调节。下面给出电机在α－β坐标系下的定子磁链计算公式，即

式中:ψs(t)为定子磁链矢量;us(t)、is(t)分别为电机定子电压矢量、电流矢量;Rs为电机定子电阻。

电机高速运行时，忽略定子电阻，可以得

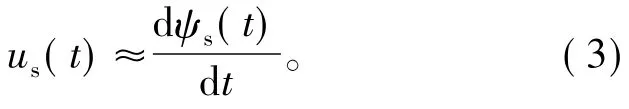
式(3)说明定子磁链的变化与逆变器产生的电压矢量有关，在电压空间矢量作用时间内，磁链将沿着电压矢量的方向运动，产生一个增量。其中所需的电压空间矢量由磁链、转矩滞环控制器和扇区选择信号共同决定，从而形成了一个开关状态表，如图2所示。定子磁链在Ⅱ扇区时，电压矢量U3和U4分别作用，使磁链矢量的幅值在滞环控制器的控制范围内，并且沿着特定的方向旋转。

由图2可知，定子磁链幅值以磁链滞环控制器的滞环宽度为允许误差脉动，很明显转矩随磁链产生脉动。而产生脉动的根源就是磁链转矩控制所采用的滞环控制器。若想从根本上减小脉动，必须摒弃滞环控制，而引入新的控制算法。

图2 传统DTC控制定子磁链轨迹Fig．2 The stator flux track of traditional DTC

2 基于空间矢量调制的DTC控制方案

2．1 DTC-SVM控制原理

为减小电动机输出转矩的脉动，改进的方案中引入PI调节器来实现磁链和转矩双闭环控制［7－9］，由于PI调节器能实现稳态无静差，克服采用滞环比较器作为控制器时磁链转矩脉动过大的缺点。

传统DTC方案，一个开关周期只有一个电压矢量起作用，不可能在一个周期中准确补偿磁链和转矩误差。若想在每一个周期中准确补偿磁链和转矩误差，必须产生任意电压空间矢量，这可通过空间矢量调制(space vector modulation，SVM)技术实现，DTC－SVM控制原理如图3所示。

图3 DTC-SVM控制原理Fig．3 The control theory diagram of DTC-SVM

可准确补偿磁链和转矩误差的任意电压矢量称为参考电压矢量Uref。本方案采用两个PI控制器对磁链和转矩进行调节，产生参考电压矢量。DTCSVM方案是在定子磁链定向坐标系下实现的，其坐标轴用d、q表示，坐标轴的旋转速度等于定子频率的同步角转速ωs。参考电压矢量在磁链定向的坐标系d－q中的分量Usd、Usq与被控量ψ、T的关系，是设计PI调节器参数的关键。

2.2 感应电机定子磁链坐标系下的数学模型

根据感应电机在三相坐标系下的电压、磁链、转矩方程，经过坐标变换，得到电机在定子磁链定向坐标系下的数学方程，该坐标系以定子磁链角速度ωs旋转，记为d－q坐标系，电机模型在d－q坐标系中的电压方程为

式中:Isd、Isq为定子电流在d－q坐标系下的分量;p为微分算子;Rr为电机转子电阻;Ird、Irq与 ψrd、ψrq分别为转子电流与磁链在d－q坐标系下的分量;ωm为转子转速。

式中:TL为负载转矩;J为转动惯量。

感应电机DTC－SVM控制方案在定子磁链定向坐标系d－q中的控制框图如图4所示，给定磁链ψ*与经过反馈计算得到的磁链ψ相比较，得到的误差信号经磁链PI调节器得到参考电压矢量在d－q坐标系下的d轴分量Usd;给定转矩信号T*与经过反馈计算得到的转矩T相比较，得到的误差信号经过转矩PI调节器得到参考电压矢量在d－q坐标系下的q轴分量Usq。根据磁动势一致的原则，经过坐标变换，将d－q坐标系下的参考电压矢量变换到两相静止坐标系α－β下，得到参考电压矢量Uref。此时，通过空间电压矢量调制(SVM)技术得到开关信号，从而驱动逆变器运行。

图4 磁链定向坐标系d-q中DTC-SVM原理Fig．4 DTC-SVM theory in stator flux coordinates d-q

为避免传统DTC控制方案中纯积分的漂移问题，可通过转子磁链计算定子磁链，感应电机中，定子磁链与转子磁链之间的关系为

2.3 磁链控制器设计

由感应电机在d－q坐标系下的电压和磁链方程［7］得

电机高速运行时转差率很小，转子转速和同步速相差不大，ωs－pbωm近似为零，可忽略最后一项，于是式(9)变为

根据式(10)得到参考电压矢量Uref在d－q坐标系中的d轴分量Usd与定子磁链ψs的关系。磁链控制回路如图5所示。

图5 磁链控制回路Fig．5 The block diagram of flux control loop

图中，

式中:Eψ(s)为磁链给定值与计算值的偏差;Kpψ与Tiψ分别为磁链PI调节器的比例系数与积分时间常数。

2.4 转矩控制器设计

由感应电机在d－q坐标系下的电压和磁链方程［7］得

根据式(15)、式(16)及式(17)得到参考电压矢量Uref在d－q坐标系中的q轴分量Usq与电磁转矩Te的关系。转矩控制回路如图6所示。

图6 转矩控制回路Fig．6 The block diagram of torque control loop

图中，

式中:ET(s)为转矩给定值与计算值的偏差;KpT与TiT分别为转矩PI调节器的比例系数与积分时间常数。

式(19)为转矩PI调节器的传递函数，转矩给定值T*与计算值T相比较，误差通过PI调节器，产生参考电压矢量的q轴分量Usq。

3 仿真和实验分析

为验证DTC－SVM控制方案的优越性，本文进行了仿真和实验分析。仿真和实验所用的异步电机参数为:额定功率为4 kW;额定电压为380 V;额定频率为50 Hz;额定转速为1 430 r/min;定子电阻为1.405 Ω;转子电阻为1.395 Ω;定子电感为0.178 H;转子电感为0.178 H;互感为0.172 2 H;电机的极对数为2;转动惯量为0.013 1 kg·m2。仿真时，给定定子磁链幅值为0.85 Wb，给定转速为1 000 r/min，给定转矩初始值为零。当t=0.004 s时，给定转矩突变为20 N·m，逆变器开关频率设置为10 kHz。

仿真和实验结果如图7～图11所示。比较图7(a)和图7(b)，在DTC－SVM方案中，由于采用SVM技术，能产生完全补偿定子磁链误差的电压矢量，采用PI调节器实现对磁链的稳态无静差控制，电机定子磁链脉动明显变小，磁链轨迹更加平滑，说明这种方法能较好地实现对磁链的控制。图8(a)和图8(b)为稳态时的电磁转矩波形，当给定转矩为20 N·m时，传统DTC方案转矩脉动是给定值的7.5%，DTC－SVM方案转矩脉动是给定值的4%，与传统DTC方案相比较转矩脉动降低3.5%。

图7 定子磁链轨迹仿真波形Fig．7 The simulation waveform of stator flux track

图8 稳态时转矩仿真波形Fig．8 The torque simulation waveform in steady state

图9(a)和图9(b)为电机稳态运行时的定子电流波形。当t=0.05 s时，电机进入稳态，定子电流脉动较小，波形比较平滑，而传统DTC方案电流脉动较大。

图9 稳态时A相电流仿真波形Fig．9 The A phase current simulation waveform in steady state

在基于TMS320LF2407 DSP的实验平台上，对空间矢量调制的DTC方案进行实验分析。将直流发电机作为模拟负载，当给定转速为1 000 r/min，给定转矩为20 N·m时，电机进入稳定运行状态，将检测的电流信号进行处理得到转矩模拟信号，通过示波器测得的转矩和A相电流波形如图10和图11所示。由仿真和实验结果可知，DTC－SVM方案能够有效减小磁链和转矩脉动，改善电机的动、静态性能。

图10 稳态时转矩实验波形Fig．10 The torque experiment waveform in steady state

图11 稳态时A相电流实验波形Fig．11 The A phase current experiment waveform in steady state

4 结语

本文针对传统DTC稳态时输出转矩脉动大，逆变器开关频率不定等问题，提出一种基于空间矢量调制的磁链、转矩双闭环直接转矩控制方案。该方案摒弃了传统DTC方案中的砰－砰控制，采用空间矢量调制方法产生任意参考电压矢量来补偿磁链误差，减小了转矩脉动，改善了电流和磁链波形，并且保证逆变器的开关频率恒定，获得了矢量控制连续平滑和直接转矩控制快速响应的优良性能。仿真和实验结果表明，DTC－SVM方案输出转矩脉动相比于传统DTC控制方案减小了3.5%，有效减小了磁链和电流波动，改善了电机的动态和静态性能。

［1］ CRISTIAN Lascu，ION Boldea，FREDE Blaabjerg．A modified direct torque control for induction motor sensorless drive［J］．IEEE Transactions on Industry Applications，2000，36(1):122－130．

［2］ GIUSEPPE S B，MARIAN P K．Direct torque control of PWM inverter-fed AC motors-a survey［J］．IEEE Transactions on Industrial Electronics，2004，51(4):744 －757．

［3］ 钱坤，谢寿生，高梅艳，等．改进的直接转矩控制在异步电动机中的应用［J］．中国电机工程学报，2004，24(7):210－214．QIAN Kun，XIE Shousheng，GAO Meiyan，et al．Improved direct torque control method for induction motor applications［J］．Proceedings of the CSEE，2004，24(7):210－214．

［4］ 张爱玲，王震宇，杨文杰．直接转矩控制系统中减小转矩脉动方案的比较［J］．电机与控制学报，2008，12(5):566－570．ZHANG Ailing，WANG Zhenyu，YANG Wenjie．Comparison between two kinds of reducing torque ripple of based on direct torque control［J］．Electric Machines and Control，2008，12(5):566 －570．

［5］ 奚国华，胡卫华，喻寿益，等．异步电机直接转矩控制模糊DSVM控制策略［J］．电机与控制学报，2006，18(2):435－449．XI Guohua，HU Weihua，YU Shouyi，et al．Fuzzy DSVM strategy in the direct torque control of an induction motor［J］．Electric Machines and Control，2006，18(2):435 －449．

［6］ OZKOP Emre，OKUMUS Halil I．Direct torque control of induction motor using space vector modulation(SVM-DTC) ［C］//2008 12th International Middle East Power System Conference，MEPCON 2008，March 12 －15，2008，Aswan，Egypt．2008:368－372．

［7］ ZELECHOWSKI M，KAZMIERKOWSKI M P，BLAABJERG F．Controller design for direct torque controlled space vector modulated(DTC-SVM)induction motor drives［C］//Proceedings of the IEEE International Symposium on Industrial Electronics，2005，June 20 －23，2005，Dubrovnik，Croatia．2005，3:951 －956．

［8］ 魏欣，陈大跃，赵春宇．基于空间矢量调制的异步电机 直接转矩控制［J］．系统仿真学报，2006，18(2):405－408．WEI Xin，CHEN Dayue，ZHAO Chunyu．Direct torque control of induction motors based on space vector modulation［J］．Journal of System Simulation，2006，18(2):405－408．

［9］ 朱琰，佘焱，姜建国．基于对称电压矢量组的直接转矩控制［J］．中国电机工程学报，2006，26(23):139－144．ZHU Yan，SHE yan，JIANG Jianguo．Direct torque control based on symmetrical voltage vectors combination［J］．Proceedings of the CSEE，2006，26(23):139－144．