一种用于三电平逆变器的双模式过调制策略
2012-01-14王建渊王琦钟彦儒
王建渊, 王琦, 钟彦儒
(西安理工大学自动化与信息工程学院,陕西西安710048)
0 引言
近年来,在大容量变频器中,相比于传统两电平逆变器,中点箝位型(neutral-point clamped,NPC)三电平逆变器由于输出电平数目较多、输出电压谐波含量较低、开关频率低、开关损耗小、器件应力小以及无须动态均压等特点,已成为当今电力电子与电力传动技术的研究热点。
20世纪90年代以前,几乎所有对SVPWM策略的研究都局限在线性调制范围内。随着人们对电机输出转矩和逆变器低压适用性要求的提高,与之相应的各种SVPWM过调制策略[1-2]在过去的20多年中得到了深入而细致的研究,如典型的单、双模式过调制、基于空间矢量分类技术过调制、基于叠加原理的SVPWM过调制等[3-4]。本文在所搭建 NPC型三电平逆变器开发平台的基础上,研究了一种在不增加任何硬件情况下的双模式过调制策略,该调制策略算法简单,能够快速和有效的确定参考电压矢量位置,将线性调制区和系统最大可能输出(六阶梯波)进行平滑衔接,使系统的输出范围由线性调制区的最大范围(SVPWM)0-90.7%扩展到0~100%,有效地提高了直流母线电压利用率。
1 NPC型三电平逆变器拓扑
图1为NPC型三电平逆变器的主电路拓扑。每相桥臂由4个主开关器件IGBT、4个续流二极管以及两个箝位二极管组成。图2为27个不同电压矢量均匀分配在α-β轴上的空间电压矢量图,大六边形的6个顶点为6个大矢量所在的位置,小六边形的每个顶点代表两个矢量(P型小矢量和N型小矢量),因此小矢量共有12个,零电压矢量由3个矢量组成,且都位于六边形的中点,其余的矢量是6个中矢量。

图1 NPC型三电平逆变器拓扑Fig.1 The topology of NPC three-level inverter
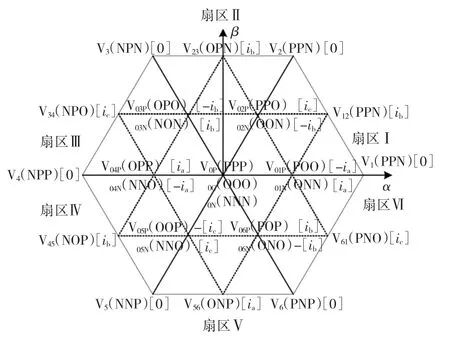
图2 三电平逆变器空间电压矢量图Fig.2 Space voltage vector map of three-level inverter
2 过调制控制策略
调制度M定义为
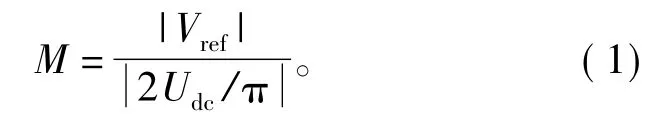
式中:Vref为参考电压矢量;Udc为逆变器直流母线电压;2Udc/π为六阶梯基波电压矢量。由于六阶梯波是最大可能输出,因此0≤M≤1。首先回顾一下传统线性调制度下的三电平SVPWM,当参考电压矢量Vref落在第一扇区B区域(图3)之内时,选择与之相邻的三个矢量对其进行合成,由伏秒平衡原理可知

其中:Ts为开关周期;Ta、Tb、Tc分别为 V01、V02、V12的作用时间。
由式(2)可得

图3 第一扇区空间电压矢量及其时间分配图Fig.3 Space voltage vector and time map of the first sector
在线性区内(M <0.907),Ts=Ta+Tb+Tc。当M=0.907时,参考电压矢量Vref的轨迹是矢量图六边形的内切圆,此时是线性调制所能达到的最大范围。当M继续增大时,参考矢量超出六边形边界的扇区,在一个开关周期内,矢量图不存在任何基本矢量组合可以在Ts时间内对Vref进行合成,实际输出的电压幅值变小并发生畸变。此时输出电压的畸变是不可避免的,然而其基波的幅值确是可以通过过调制技术得到补偿的[3,5-6]。经过补偿的输出电压基波就能够准确的跟踪指令电压。当然,补偿结果的上限是六阶梯波的基波幅值2Udc/π。对于SVPWM,补偿的手段是对参考电压矢量的幅值和相位进行合适的修正,以获得恰当的补偿量。因此,三电平SVPWM过调制策略的关键就是找到合适的电压矢量的修正算法,以及调制度M与幅值修正量和相位修正量之间的对应关系,使得线性调制区和系统最大可能输出(六阶梯波)进行平滑衔接。以下为过调制下三电平SVPWM 的双模式调制策略[7-9]。
2.1 过调制策略Ⅰ(0.907<M≤0.953 5)
在如图4所示,在每个扇区内都有两个典型的区域:Q和R。首先,在区域Q中,由于实际参考矢量Vref已经超出了六边形边界,在一个开关周期Ts内,矢量图不存在任何基本矢量组合可以在Ts时间内对Vref进行合成,导致在此部分实际输出电压发生衰减。其次,在区域R中,参考矢量Vref与六边形边界之间有一段距离,有足够的区域使得存在基本矢量组合可以在Ts时间内对Vref进行合成。因此,可以考虑将R部分扇区的参考矢量幅值增大,在一个线电压周期中用R扇区部分增大的电压幅值去抵消Q部分所造成的电压损失。当调制度介于0.907和0.953 5时,称为过调制模式I[7-9]。图4中,粗虚线部分表示实际参考电压矢量Vref在过调制模式I下的实际轨迹,此时Vref的轨迹超出了六边形边界,为了补偿过调制时的输出电压损失,对Vref的幅值和相位进行了合适的修正,修正后的参考电压矢量沿着轨迹LMNP运行,如图4中粗黑线所示。首先,在R部分,沿着圆形轨迹LM运行,然后,在Q部分沿着六边形上MN直线轨迹运行,最后再沿着圆形轨迹NP运行。因此,的旋转轨迹为LM段圆弧,MN段六边形的边,NP段圆弧。θ1为与六边形夹角,由文献[8-9]可知,角度 θ1为
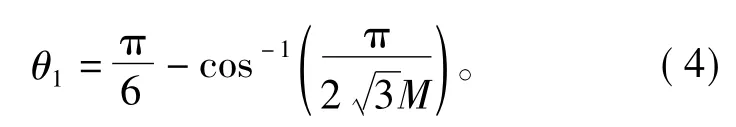
由式(4)可以看出,对于任意一个给定的调制度M,角度θ1都是唯一的,因此没有必要在每个开关周期都计算角度θ1,以下为修正后参考矢量分别位于圆弧LM和NP部分以及六边形直线MN部分时作用时间的计算。
1)直线 MN 部分(θ1≤θ≤π/3 - θ1)
在直线MN部分,每个开关周期内,两个电压矢量将被选择。在三角形C中,电压矢量V1和V12将被选择来合成参考矢量。在三角形D中,电压矢量V12和V2将被选择来合成参考矢量。在三角形C和D中的作用时间计算为

图4 过调制I下第一扇区空间电压矢量分配图Fig.4 Space voltage vector map of the first sector in overmodulation I

确定;
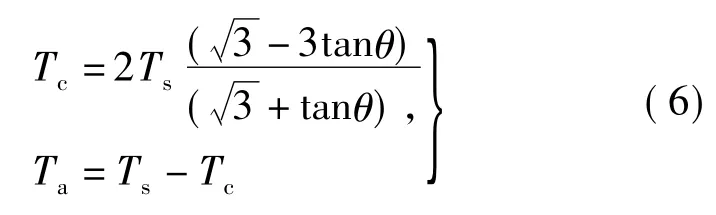
确定。
2)圆弧LM和NP部分(0≤θ<θ1和π/3-θ1<θ≤π/3
在圆弧部分,一个线电压周期中需要用圆弧R扇区部分增大的电压幅值去补偿过调制时Q部分所造成的电压损失。为了补偿Q部分的作用时间,引入了补偿系数λ。补偿系数λ被定义为在满足伏秒平衡原理基础上,电压实际损失与最大损失之比。在线性调制区内,最大调制系数为0.907。在过调制区内,对于任意的一个调制度M,实际损失的是(M-0.907)。对在过调制Ⅰ(0.907<M≤0.953 5)时,最大损失为(0.9535-0.907)。因此λ定义为

当0.907<M≤0.953 5时,补偿系数λ取值范围为[0,1]。由式(7)可以看出,对于任意一个给定的调制度M,补偿系数λ都是一个固定值。因此,不必在每个调制周期中计算λ的值。圆弧LM和NP部分作用时间分别表示为

式中:Ta、Tb和Tc为线性调制区(M≤0.907)时的作用时间;Tam、Tbm和 Tcm为过调制 I(0.907<M≤0.953 5)时修正后的作用时间;λ为补偿系数。
2.2 过调制策略Ⅱ(0.953 5<M≤1)
随着调制度的增加,留给R部分用于补偿Q部分电压损失的余量越来越小。当余量等于零时,用过调制策略I已不可能再补偿Q部分的电压损失,此时实际参考电压矢量Vref的运行轨迹是六边形的边界。当调制度超过0.953 5时,称为过调制模式II[7-9]。图 5 中,Vref超出大六边形,整个运行轨迹都在六边形外部。输出电压的衰减已经不能够由线性区补偿,即在R区域不存在任何基本矢量组合可以在一个开关周期Ts时间内对Vref进行合成,更不可能补偿由Q区域所带来的电压损失。因此,补偿的手段是对参考电压矢量的幅值和相位进行合适的修正,以获得恰当的补偿量。修正后的参考电压矢量如图5所示,圆弧部分轨迹消失,沿着直线轨迹LM、PQ、SL运行,如图5中粗黑线所示。引入了保持角θ2,通常θ2是通过查表方式获得的一个非线性函数,由文献[8-9]可知,θ2是一个有关M的函数方程,即
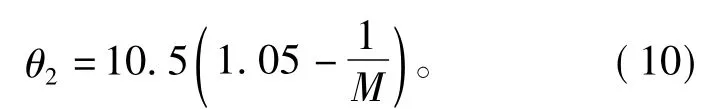

图5 过调制II下第I扇区时空间电压矢量分配图Fig.5 Space voltage vector map of the first sector in overmodulation II
由式(10)可以看出,对于任意一个给定的调制度M,θ2都是一个固定值。直线LM、PQ、SL部分作用时间计算如下
1)直线 PQ 部分(θ2≤θ≤π/3- θ2):当修正后的参考电压矢量相位角大于θ2并且小于π/3-θ2时,沿着直线PQ运行,对于直线轨迹,作用时间的计算与过调制I时的直线部分类似,计算公式为式(5)和式(6)。
2)直线LM和SL部分(0≤θ<θ2和π/3-θ2<θ≤π/3):当修正后参考电压矢量的相位角小于θ2(0≤θ<θ2)时的相位一直保持在0°,实际参考电压矢量位于LM直线上。当的相位角大于π/3-θ2并且小于 π/3(π/3-θ2<θ≤π/3)时,的相位一直保持在π/3上,即参考电压矢量位于SL直线上。作用时间为
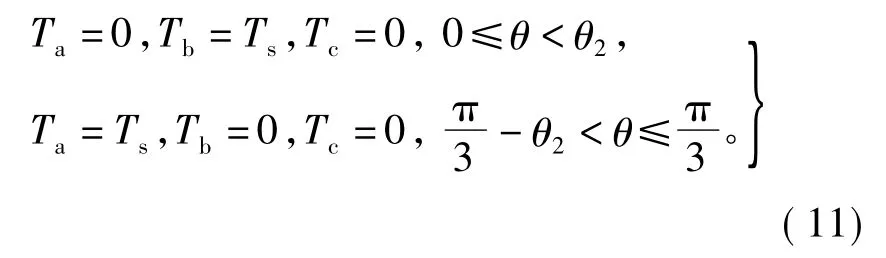
3 系统实现
图6和图7分别是以DSP芯片TMS320F28335为控制核心新搭建的实验样机以及系统结构框图,主要包括主电路、驱动电路、检测电路、保护电路、电源模块和控制器等几部分。主电路采用典型的AC-DC-AC变换电路;以TMS320F28335为控制器输出的12路两两互补的PWM正好对应三电平逆变器的12个功率管;驱动电路是则是将控制器所输出的12路PWM信号采用光耦隔离后驱动IGBT开通与关断;电源模块独立提供12路隔离驱动电源以及控制器正常工作所需电源。

图6 实验样机Fig.6 Experimental prototype
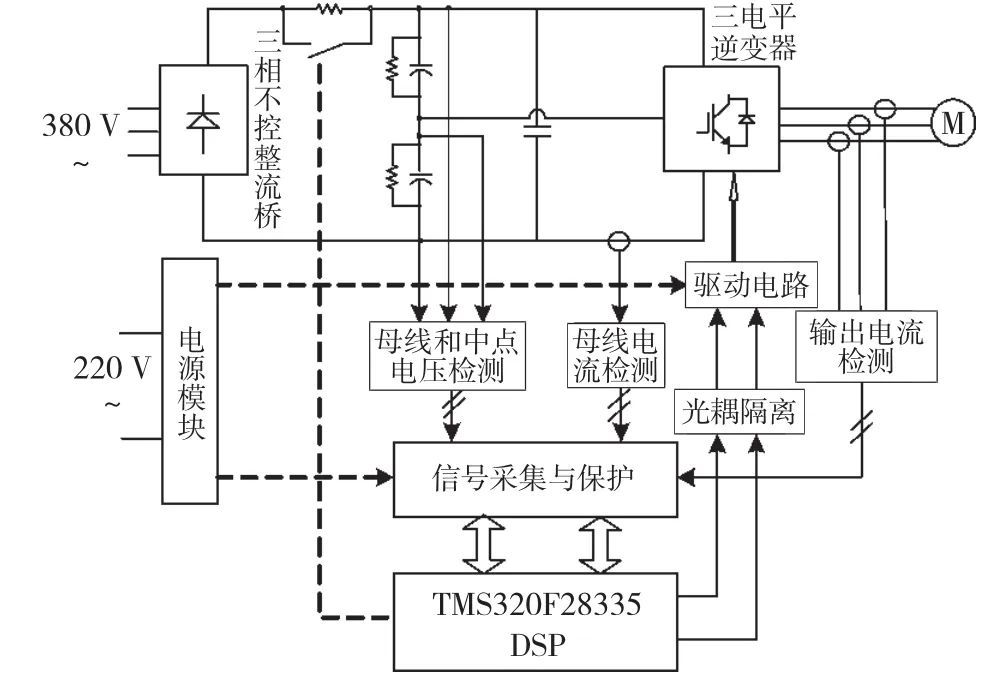
图7 系统结构框图Fig.7 The system frame
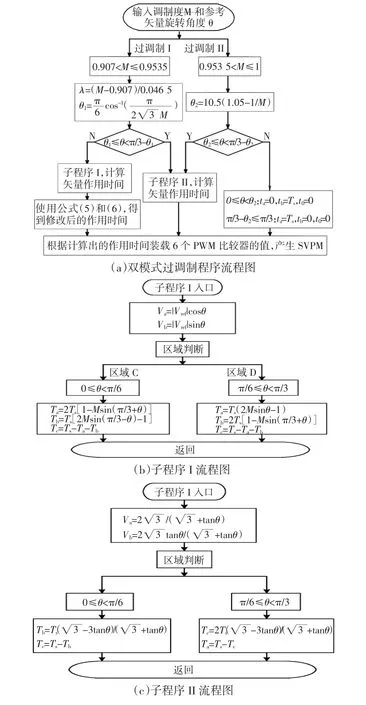
图8 系统软件流程图Fig.8 Software flow chart of system
图8为系统控制软件部分流程图。程序主要分为3部分:寄存器、变量、常量和常用宏定义部分、主程序部分、中断控制部分。主程序部分主要完成各种初始化和设置等实时性要求不高的部分,而本文核心的双模式SVPWM过调制算法以及采样和保护等实时性要求高的部分放在中断子程序中执行。
4 实验验证
为了验证所研究双模式过调制策略的可行性和有效性,在搭建的以一片TMS320F28335DSP为基础的NPC型三电平原理样机上进行了实验,实验参数如表1所示。
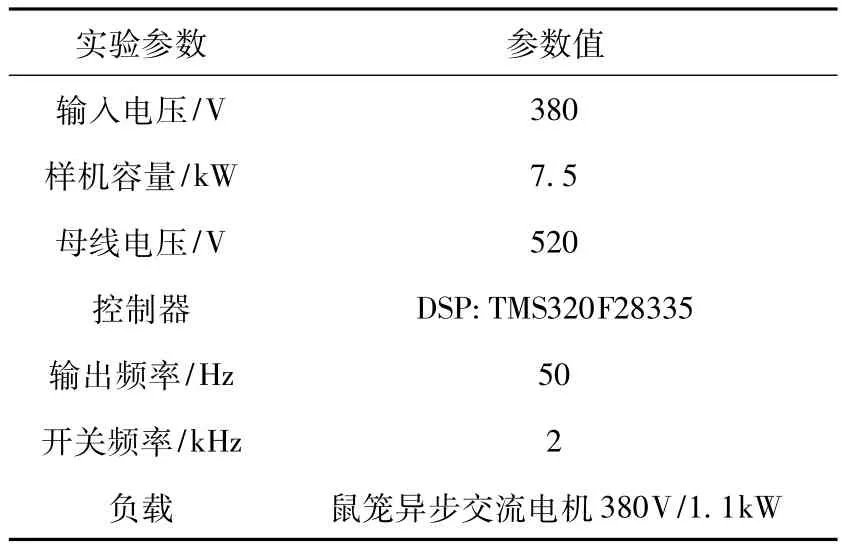
表1 实验参数Table 1 Experimental parameters
图 9(a)、(b)、(c)、(d)分别线性调制度(M=0.6)、过调制I(M=0.93)、过调制 II(M=0.98)以及最大调制度(M=1.0)下,输出频率为50 Hz时,输出线电压Uab和相电流Ia的实验波形;由线电压Uab和相电流Ia波形可以看出,随着调制度的增大其输出电压逐渐趋向方波,直到最大调制度(M=1.0)下,系统输出电压为最大可能输出(六阶梯波)。过调制方法使逆变器输出电压产生失真,导致输出电流失真,输出电流增大,并且在进入过调制时电流波形脉动变大。
图10(a)~(d)给出了不同调制度时输出线电压和相电流波形的FFT分析,可以看出随着调制度的增大,输出电流的幅值在增大,但THD也在逐步升高。由线电压和相电流谐波分析可知,该双模式过调制策略能够提高逆变器输出电压和电流,使直流母线电压利用率达到最大,能够获得高转矩输出。然而这些优点的得到是以引入不可避免的高次谐波为代价的,因此在一般情况下应该限制调制比,只有在要求瞬时驱动能力增大的场合下才进入过调制状态,使系统具有良好的过调制特性。

图9 不同调制度时输出线电压和相电流波形Fig.9 The waveforms of output line-to-line voltage and phase current under different modulation
5 结语

图10 不同调制度下输出线电压和相电流谐波分析Fig.10 The harmonic analysis of output line-to-line voltage and phase current under different modulation
研究了一种NPC型三电平逆变器由线性调制到过调制下的双模式过调制策略,采用一种相对简洁的电压矢量作用时间计算方法,快速和有效的确定了参考电压矢量位置,分析了其调制算法的实现过程。在搭建的NPC型三电平逆变器开发平台上对该策略进行了实验验证。实验结果表明,该双模式过调制策略能够使得直流母线电压利用率达到最大,提高逆变器输出电压,获得高转矩输出。虽然这些收益的得到是以引入不可避免的高次谐波为代价的,但是相对于许多实际的应用,这一代价还是值得的。
[1] 李阳,戴鹏,于月森,等.三电平逆变器SVPWM过调制控制策略综述[J].电气传动,2010,40(7):8 -11.LI Yang,DAI Peng,YU Yuesen,et al.Overview of the SVPWM overmodulation strategies of three-level inverter[J].Electric Drive,2010,40(7):8 -11.
[2] N HO N V.Two-mode overmodulation in two-level voltage source inverter using principle control between limit trajectories[C]//Proceedings of PEDS2003,Nov 17-Nov 20,2003,Novotel A-pollo Hotel,Singapore.2003:1274 -1279.
[3] SUBRATA K MONDAL,BIMALK BOSE,VALENTIN OLES-CHUK.Space vector pulse width modulation of three-level inverter extending oper-ation into overmodulation region[J].IEEE Trancactions on Power Electronics,2003,18(2):604 -611.
[4] CHEN YIE-TONE,MEMBER,LIN HUNG-TSE.Analysis and implemen-tation of a novel space vector modulation strategy for multilevel inverter about the operations in the overmodulation region[J].IEEE International Symposium on Power Electronics for Distributed G -eneration Systems,2010:417-422.
[5] LEE DONGCHOON,LEE GMYOUNG.A novel overmodulation technique for space-vector PWM inverters[J].IEEE Trancactions on Power Electronics,1998,13(6):1144 -1151.
[6] ANSHUMA TRIPATHI,ASHWIN M KHMBADKONE.Direct method of overmodulation with integrated closed loop stator flux vector control[J].IEEE Trancactions on Power Electronics,2005,20(5):1161-1168.
[7] 金舜,钟彦儒,程为彬.新颖的 SVPWM过调制策略及其在三电平逆变器中的应用[J].中国电机工程学报,2006,26(20):84-90.JIN Shun,ZHONG Yanru,CHENG Weibin.Novel SVPWM overmodulation scheme and its application in three - level inverter[J].Proceedings of the CSEE,2006,26(20):84 -90.
[8] GUPTA A K,KHMBADKONE A M.A general space vector PWM algorithm for a multilevel inverter including operation in overmdulation range,with a detailed modulation analysis for a 3-level NPC inverter[J].IEEE Trancactions on Power Electronics,2005,20(5):2527-2533.
[9] GUPTA A K,KHMBADKONE A M.A simple space vector PWM scheme to operate a three-level NPC inverter at high modulation index including overmodulation region,with neutral point balancing[J].IEEE Trancactions on Power Electronics,2007,43(3):751-760.
