测量设备轴角编码器误差修正研究

钟德安，包 飞，张同双，冯鸿奎，刘 扬

(中国卫星海上测控部，江苏江阴214431)

0 引言

角度测量是由轴角编码器(角度编码装置)来完成，其基本功能是把天线2个轴的机械转角变为数字量的角度数据输出［1］。轴角编码器是测量设备重要的测角部件，其精度对测量设备总精度产生直接影响。一般要求轴角编码器精度比测量设备总精度高3～10倍［2］。影响轴角编码器精度的因素很多，如度码盘和旋转变压器的轴与天线机械轴间的耦合精度及同心度、数码读出电路、传感器电路等。目前对轴角编码器的误差有多种处理方法:文献［3］给出的测量设备测角系统误差修正模型中未考虑对轴角编码器误差的修正;文献［4］仅考虑了轴角编码器由于安装时与旋转轴的同心度不准造成的偏心误差的修正;文献［5］以正弦规律的形式给出了轴角编码器造成的误差修正模型。从实际检测情况看，由于轴角编码器误差因素的复杂性，安装在不同测量设备上的轴角编码器虽然工作原理相同，但误差规律不尽相同。有的轴角编码器虽然其总的精度满足指标要求，但在某些角度范围内的误差远低于其精度指标，如果误差修正方法和修正模型应用不当，对这一角度范围内测量数据的精度将产生较大影响。因此，应根据误差实际检测情况采用不同的修正方法和模型加以修正。

本文列举了3个轴角编码器误差检测例子，通过分析其误差规律和采用不同的修正模型，使轴角编码器测量值均方根误差分别降低了7.2″、1.8″和1.6″。

1 轴角编码器工作原理

轴角编码器有直接角度编码器和间接角度编码器2种类型。直接角度编码器将天线轴的角位移直接转换为数字化角度数据，可分为直读式码盘(如接触式码盘或光电码盘［6］)和“增量积累”的增量码盘;而间接角度编码器是先将天线机械轴的转角通过传感器(如电位器、旋转变压器)变为连续的物理量(电压、时间间隔)，然后再转换为数字化角度数据。光电码盘和用旋转变压器作角位移传感器的编码器是比较普遍采用的轴角编码器。因产生的角度数据都代表着当前机械轴角位移，因此码盘和旋转变压器的轴必须与天线的机械轴作硬连接，通常采用套轴式联接，以提高它们之间的耦合精度。

直接角度测量是由编码装置和数码读出电路2部分完成。编码装置由编码盘和固定的敏感元件组成，编码盘直接或通过随动系统与天线机械轴相连，而输出数码则从敏感元件取得。数码读出电路的作用是从敏感元件读取角度数码。

常见的间接角度测量是用旋转变压器作为角位移的敏感元件(角度传感器)，其编码原理是将天线轴的机械转角用一对幅度随转角正弦和余弦变化的交流电压反映出来，有这一对正余弦电压即可形成天线轴转角的数码。一般称轴角编码器为天线轴角位置显示单元。轴角编码器采用分解器—数字转换器(Resover-to-Digital Converter RDC)实现对旋转变压器输出的模拟信号到数字信号的转换，RDC是一个锁相环，其数字输出角度将自动地跟踪天线的机械转角。

2 轴角编码器误差检测方法

2.1 方法原理

对轴角编码器精度检测采用与高精度测角仪器直接比对的方法。以方位轴角编码器为例，作为检测标准的高精度经纬仪与测量设备同时测量同一个固定目标，对测量数据进行比对作差，统计方位轴角编码器精度。

2.2 检测步骤

采用经纬仪检测方位轴角编码器精度包括以下步骤:

①将经纬仪安装在测量设备方位旋转中心顶部，并仔细调整其竖轴与天线方位轴重合，以减少测量设备方位转盘倾斜对经纬仪读数的影响;

②经纬仪对准一个距离大于1 km、仰角近似为零度的固定目标，读取方位编码器数据Aci和经纬仪数据Aji;

③顺时针或逆时针转动天线方位，每转15°左右停转，经纬仪重新瞄准同一目标，再读取方位编码器数据和经纬仪数据;

④按下式计算方位轴角编码器精度:

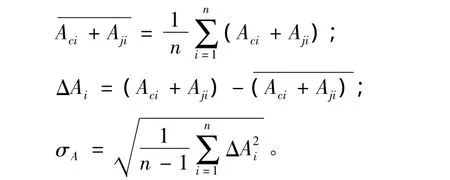
3 轴角编码器误差检测举例

利用上述检测方法分别对3套测量设备的方位轴角编码器误差进行了检测，3套均为用旋转变压器作为角位移敏感元件的间接式角度编码器。三套轴角编码器检测得到的残差数据如表1、表2和表3所示。

根据检测数据可算得A、B、C三套编码器测量值均方根误差分别为 11.2″、12.2″和 10.8″。

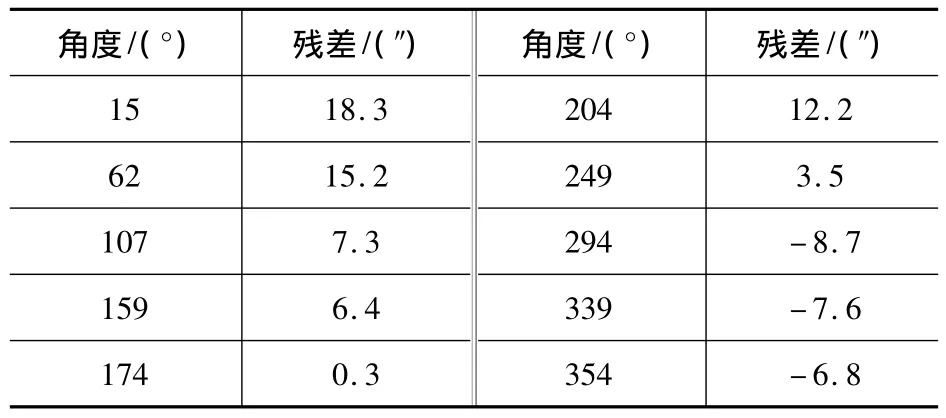
表1 A套轴角编码器方位残差数据

表2 B套轴角编码器方位残差数据

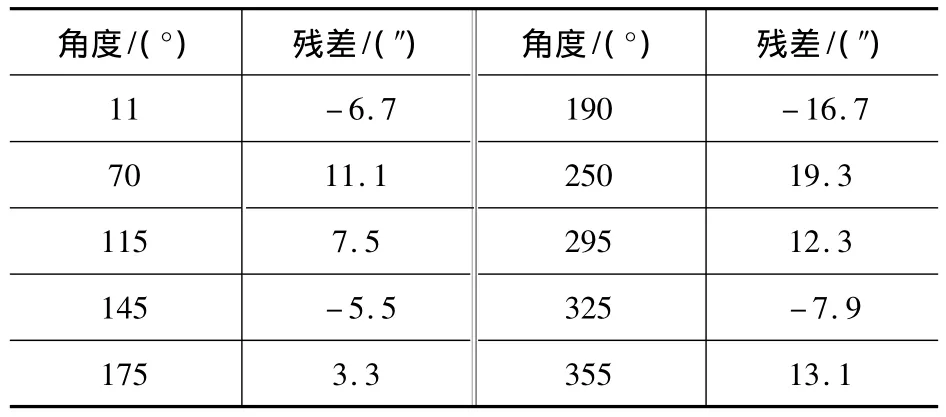
表3 C套轴角编码器方位残差数据

4 轴角编码器误差修正

图1、图2和图3分别为A、B、C三套编码器的残差图(图中散点用“▲”所示)。可以看出，A套编码器在方位角15°～204°之间的残差为正值，其余为负值;B套、C套则正负相间无明显规律。同时也可看出，残差曲线并没有呈现出典型的正弦或余弦型偏心误差规律。因此，应根据对编码器的实际检测结果，采用不同的方法和模型加以修正。

通用的测量设备方位角误差修正公式如下:

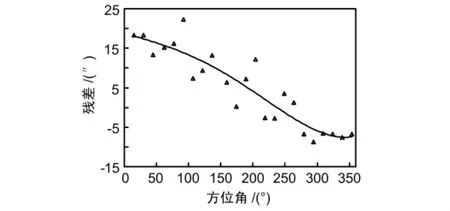
图1 A套编码器的残差

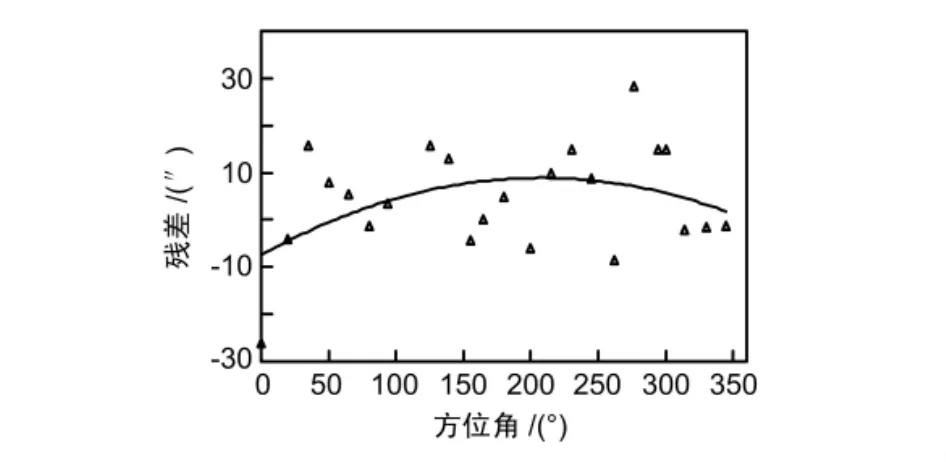
图2 B套编码器的残差

图3 C套编码器的残差

式中，A为经轴系误差、零位及编码器误差修正后的方位角;Ac为测量设备轴角编码器方位角输出值;A0为方位零位;βm、Am分别为大盘最大倾斜量和最大倾斜方向;Ec为测量设备轴角编码器俯仰角输出值;δm为两轴不正交;Sb为光机偏差;Cs为方位光电偏差;ΔUA为方位误差电压;CA为方位支路定向灵敏度;fb(Ac)为方位编码器误差模型。

图1、图2、图3中的连续曲线分别为根据A、B、C三套编码器残差进行拟合的编码器误差模型。

A套编码器误差模型为:

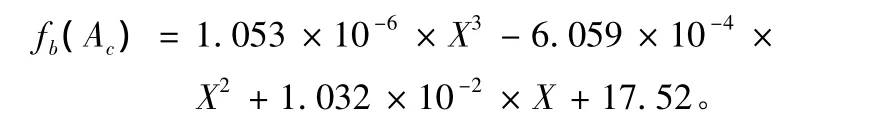
B套编码器误差模型为:

C套编码器误差模型:

经过拟合修正后，A、B、C三套编码器测量值的均方根误差分别为 4″、10.4″和 9.2″，与修正前相比分别降低了7.2″、1.8″和 1.6″。

5 结束语

轴角编码器误差对测量设备的测量精度有直接影响，有些轴角编码器虽然其总的精度满足指标要求，但在某些局部角度范围内的均方根误差可远超其精度指标，应根据实际检测结果对其进行修正。

由于航天器飞行轨道有自身的规律，对可移动测量设备应避开编码器误差较大的区域范围。对固定台站可根据对航天器测量的实际角度范围，对编码器误差进行分段拟合并加以修正，进一步提高测量精度。

通过增加检测点数、采用不同的修正方法和模型可进一步提高轴角编码器误差修正精度。

［1］赵业福.无线电跟踪测量［M］.北京:国防工业出版社，2003.

［2］江文达.陈道桂.航天测量船［M］.北京:国防工业出版社，2002.

［3］杨斌峰.地面测控雷达角度标校技术［J］.现代电子技术，2005(17):47-52.

［4］吕亚强.单脉冲雷达测量误差修正方法研究［J］.计算机测量与控制，2008(8):1 155-1 157.

［5］袁 勇.雷达的卫星标定技术方法［J］.陕西科技大学学报，2008(4):109-113.

［6］罗世魁，王国强.伪随机码在绝对式光电轴角编码器中的应用［J］.光学精密工程，2003(6):596-601.