基于LS－RVR误差补偿的动态矩阵控制

赵铁彪，徐毅，樊培利，薛美盛

（1.中国科学技术大学自动化系，合肥230026；2.山东石横发电厂，山东泰安271261）

动态矩阵控制（DMC）是一种重要的预测控制算法，由Cutlergf在1980年提出［1］。它采用在工程上易于测取的对象阶跃响应做模型，算法比较简单，计算量较少，鲁棒性较强，适用于有纯时延、开环渐进稳定的非最小相位系统，近年来已在冶金、石油、化工等部门的过程控制中取得成功的应用［2］。研究发现，DMC对模型失配的鲁棒性有一定的局限性，需要改善预测模型，从而使得预测输出值更准确。

文献［3－4］中提到，由于先验知识的局限性和过程的时变性，因而模型误差势必降低系统的控制精度和鲁棒性，必须采取附加的预测手段弥补模型预测的不足。针对这个问题，席裕庚提出了引入误差预测，采用误差预测和模型预测相结合的思路。文献［5］中，基于BP结构神经网络，对系统的建模误差进行预测，取得了一定的效果。文献［6］中，提出用小波网络建立误差的预测模型，并对模型预测进行动态补偿，增强了系统鲁棒性。文献［7］中将LS－SVM支持向量机用于广义预测控制的误差补偿，取得了一定的效果。然而，支持向量机建模也存在一定不足，如基函数必须满足mercer定理等。文献［8］提出一种新的机器学习方法最小二乘相关向量回归（LS－RVR），并将其与支持向量机（SVM）模型、相关向量回归（RVR）模型分别就计算复杂度和模型精度做了比较，获得了更良好的建模效果。

笔者针对动态矩阵控制中遇到的模型失配问题，结合相关向量回归的特点，提出了基于LS－

RVR的误差补偿动态矩阵控制算法，并进行了仿真实验，实验结果表明了该算法的有效性。

1 动态矩阵控制

1.1 预测模型

假设未来M个时刻的控制增量分别为Δu（k），Δu（k＋1），…，Δu（k＋M－1），则未来P个时刻系统的预测模型输出值为

式中：Ym（k＋1）——k时刻施加Δu（k）时未来N个时刻的模型预测值，Ym（k＋1）＝［ym（k＋1／k），ym（k＋2／k），…，ym（k＋N／k）］T；Y0（k＋1）——k时刻未施加Δu（k）时未来N个时刻的模型输出初值，Y0（k＋1）＝［y0（k＋1／k），y0（k＋2／k），…，y0（k＋N／k）］T；ΔU（k）＝［Δu（k），Δu（k＋1），…，Δu（k＋M－1）］T；A——动态矩阵，

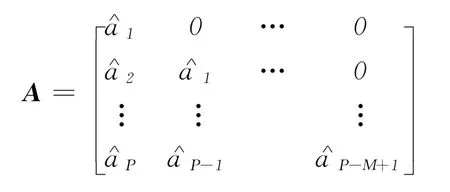
模型输出初值：

式中：U（k－1）＝［u（k－N＋1），u（k－N＋2），…，u（k－1）］T。将式（2）代入式（1）中，即可求出未来N个时刻预测模型输出值为

1.2 反馈校正

为了克服模型误差和干扰等的影响，需要用实际输出误差对系统预测模型输出进行修正，得到预测输出值，即：

式中：Yp（k＋1）＝［yp（k＋1），yp（k＋2），…，yp（k＋P）］T；H＝［h1，h2，…，hP］T。

1.3 滚动优化

最优控制律由二次型性能指标确定：

由∂JP／∂ΔU（k）＝0，求得：

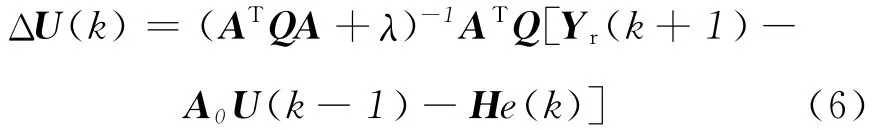
式中：e（k）＝y（k）－ym（k）。将上式展开，可求得从k到k＋M－1时刻的控制增量，即：

2 最小二乘相关向量回归

2.1 RVR

RVR是文献［10］提出的一种贝叶斯框架，可以用来获得回归建模的稀疏解。与SVM相比，RVR使用更少的基函数；不仅可以得到预测输出的点估计，还可以得到预测输出的概率分布。另外，基函数无须满足mercer定理［10－11］。

设广义线性模型：

式中：K（x，xi）——基函数；wi——模型的权值向量的第i个元素。假设输入输出样本集

输出值是来自有附加噪声模型的采样值：

εn服从方差为σ2的零均值高斯分布，则样本集的似然函数为［10］

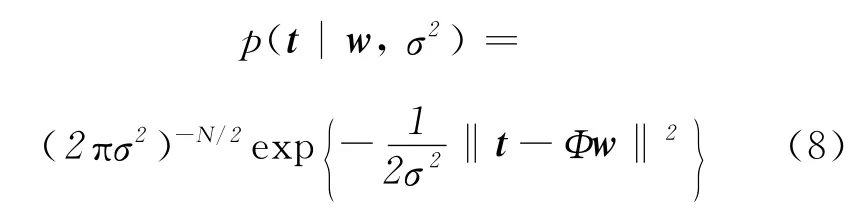
式中：t＝（t1，t2，…，tN）；w＝（w1，w2，…，wN）；Φ——设计矩阵，Φ∈N×（N＋1），Φ＝［φ（x1），φ（x2），…，φ（xN）］T。其中，φ（xn）＝［1，K（xn，x1），K（xn，x2），…，K（xn，xN）］T。对权值向量定义先验的概率密度分布，即：

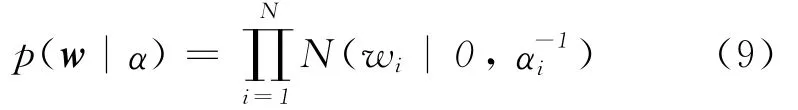
式中：α——N＋1维向量，被称为超参数，它使得回归模型的复杂程度降低并更为光滑。由贝叶斯准则，可以得到权值向量的后验似然分布为

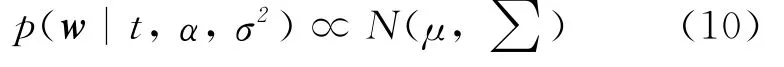
对式（10）两端取对数，得：

分别对α和σ2求导，并令导数等于0，可以得到公式［10］：

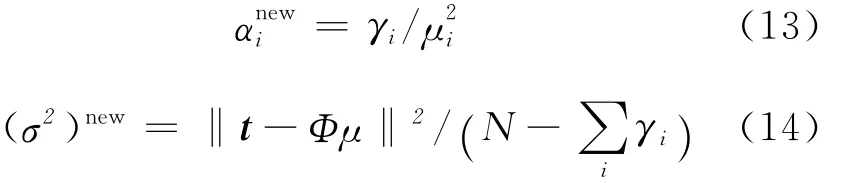
2.2 LS－RVR

对于采样获得的输入输出数据，先进行最小二乘线性建模，然后把该线性模型的拟合误差和输入输出数据用RVR进行建模，从而构成整个LSRVR模型［8］。

对于n阶系统，假设输入输出序列为｛u（k），y（k）｝k＝1，2，…，n＋N，则有：

式中：Y＝［y（n＋1），y（n＋2），…，y（n＋N）］T；

运用LS－RVR建模步骤如下：

a）运用标准递推最小二乘方法建模，根据建立的模型可以得出对于输入X，模型输出为

b）最小二乘方法建模误差为

c）运用RVR方法对E进行建模，求得模型权值向量序列和相关向量序列｛wk｝，｛xk｝，k＝1，2，…，m，其中m为相关向量的个数。有：

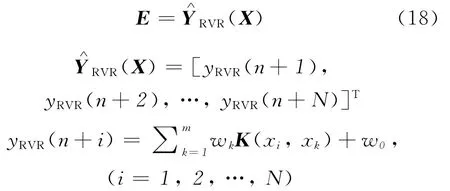
d）对于一个未知点x＊，建立模型的输出结果为

3 误差补偿动态矩阵控制

为了克服模型误差和干扰的影响，DMC算法采用该步系统实际输出与模型预测输出的误差来代替下一步模型预测输出的误差，增加了模型预测输出精度，但它对建模误差的修正仍有一定的局限性。为了提高模型预测精度，笔者提出了基于LSRVR误差补偿算法，对历史输入输出和误差进行训练，建立误差模型并对误差进行一步预测得到下一步的模型预测误差，从而提高了模型预测的精度。

利用LS－RVR建模方法，建立误差模型。该误差模型可以表示为［7］

根据得到的误差模型，预测下步的误差：

从而可得控制增量输出为

计算步骤：

a）对预测控制参数进行初始化。

b）进行传统动态矩阵控制，得到输入、输出、误差数据，作为训练样本。

c）对误差数据进行建模，得到误差模型。

d）根据误差模型，采用式（22）描述的控制律进行动态矩阵控制。

4 仿真实验

例1 选取具有大惯性的火电厂热工系统主蒸汽压力对象［12］，其传递函数为

采样周期为5s，预测前景为90，控制前景为15，误差矩阵hi＝1，控制加权矩阵λi＝1。

离散化后，由于实际系统中存在一定的扰动，假设实际模型为

预测模型为

仿真结果如图1～3所示，纵坐标变量为无量纲。

图1 传统DMC方法

图2 LS－RVR误差补偿DMC方法

图3 两种方法输出比较

例2 选取仿真对象为文献［13］给出的山东石横电厂2号炉主汽温过程，在高负荷（270～315MW）时模型对象：

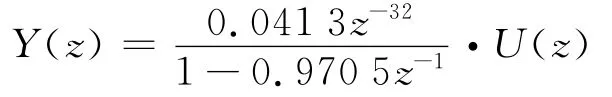
采样时间选4s，预测前景为130，控制前景为15，误差矩阵hi＝1，控制加权矩阵λi＝1。

由于实际系统中存在一定的扰动，假设实际模型为

预测模型为

仿真结果如图4～6所示，纵坐标变量为无量纲。

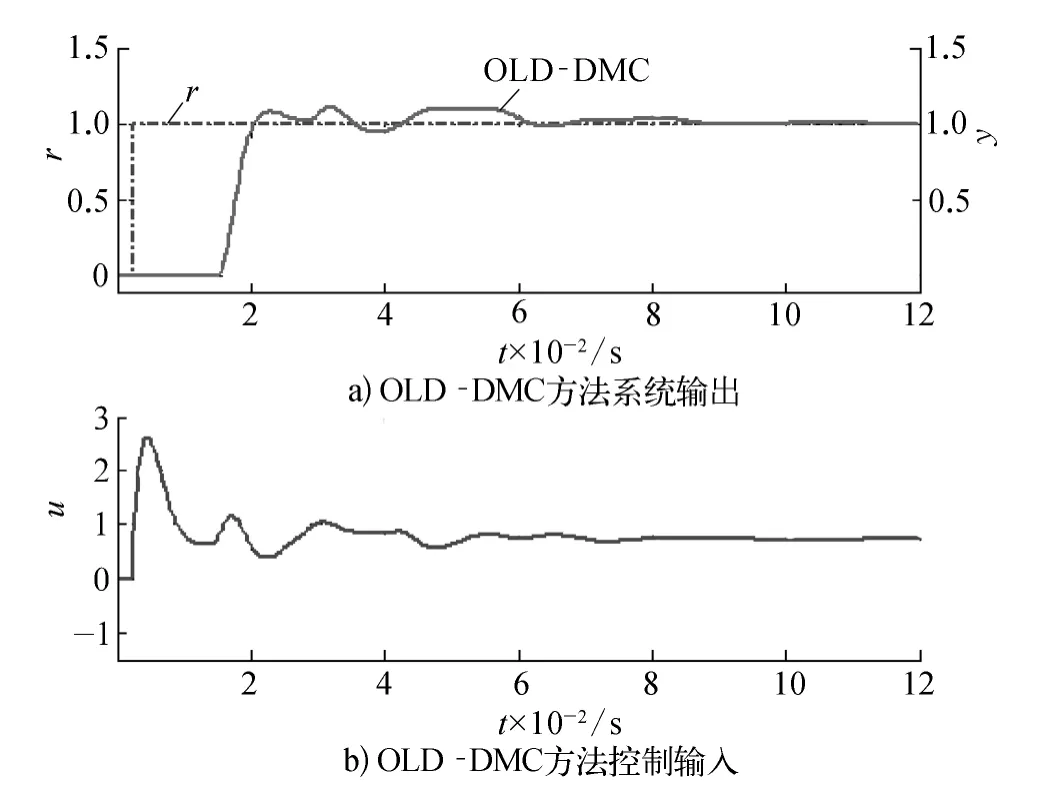
图4 传统DMC方法

由仿真结果可以看出，误差补偿型预测控制算法与传统动态矩阵控制算法相比，控制效果得到进一步提高。

图5 LS－RVR误差补偿DMC方法

图6 两种方法输出比较

5 结束语

笔者针对传统DMC控制对于模型失配的鲁棒性有一定的局限性，提出新的LS－RVR误差补偿动态矩阵控制算法。通过LS－RVR良好的建模能力，对误差与历史输入输出进行模型建模，从而提高预测输出的精度，提高控制性能。仿真结果表明，该算法改善了系统在模型失配情况下的控制效果。

［1］ CUTLER C R，RAMAKER B L.Dynamic Matrix Control－a Computer Control Algorithm［C］.Proc.Joint Automatic Control Conf.CA；San Francisco，1980.

［2］ 舒迪前.预测控制系统及应用［M］.北京：机械工业出版社，1996：127－132.

［3］ 席裕庚，许晓鸣，张钟俊.预测控制的研究现状和多层智能预测控制［J］.控制理论与应用，1989，6（02）：1－7.

［4］ 席裕庚.关于预测控制的进一步思考［J］.控制理论与应用，1994，11（02）：219－221.

［5］ 李少远，刘浩，袁著祉.基于神经网络误差修正的广义预测控制［J］.控制理论与应用，1996，13（05）：677－680.

［6］ 王群仙，李少远，李焕芝，等.基于小波网络动态补偿的广义预测控制器［J］.自动化学报，1999，9（05）：701－704.

［7］ 翟永杰，李海丽，王东风，等.LS－SVM误差补偿的广义预测控制［J］.计算机工程，2010，46（03）：24－27.

［8］ 陶呈纲.基于相关向量回归模型的预测控制研究［D］.合肥：中国科学技术大学，2011：18－20.

［9］ 席裕庚.预测控制［M］.北京：国防工业出版社，1993：11－18.

［10］ 吴冰，程思微，张文琼，等.基于相关向量回归的仿真元建模方法［J］.计算机工程，2010，36（03）：24－27.

［11］ TIPPING M E.Sparse Bayesian Learning and the Relevance Vector Machine［J］.Journal of Machine Learning Research，2001，1（03）：211－214.

［12］ WANG D F，HAN P，REN Q.Chaos Optimization Variable Arguments PID Controller and Its Application to Main Steam Pressure Regulating System［C］／／2002International Conference on Machine Learning and Cybernetics，2002：2116－2120.

［13］ 弓岱伟.先进控制与优化软件的设计及在电站锅炉汽温预测控制中的应用［D］.合肥：中国科学技术大学，2008：68－70.