＊ 两类3－正则图的邻点可区别I－全染色

杨随义，杨晓亚，唐保祥，何万生

（天水师范学院 数学与统计学院，甘肃 天水 741001）

＊两类3－正则图的邻点可区别I－全染色

杨随义，杨晓亚，唐保祥，何万生

（天水师范学院 数学与统计学院，甘肃 天水 741001）

图G的I－全染色是指若干种颜色对图G的顶点和边的一个分配，使得任意两个相邻的点的颜色不同，任意两条相邻的边的颜色不同.在图G的一个I－全染色下，G的任意一个点的色集合是指该点的颜色以及与该点相关联的全体边的颜色构成的集合.图G的一个I－全染色称为是邻点可区别的，如果任意两个相邻点的色集合不相等.对一个图G进行邻点可区别I－全染色所用的最少颜色的数目称为图G的邻点可区别I－全色数.本文给出了两类3－正则图的邻点可区别I－全色数.

I－全染色；邻点可区别I－全染色；邻点可区别I－全色数

图的染色是图论的重要研究内容之一，由计算机科学和信息科学等所产生的点可区别边染色［1］，邻点可区别边染色（或邻强边染色）［2］，及邻点可区别全染色［3－6］等都是十分困难的问题，至今文献甚少.在此基础上，进一步提出了图的新染色概念.图的邻点可区别I－全染色是其中之一［7］，本文给出了两类3－正则图的邻点可区别I－全色数.

定义1.1［6］设G是阶至少为2的连通图，k为正整数，f是图G的使用颜色为1，2，…，k的正常全染色.对∀x∈V（G），令C（x）表示在f下点x的颜色及与x关联的全体边的颜色构成的集合，称之为在全染色f下点x的色集合，令¯C（x）＝｛1，2，…，k｝＼C（x）.如果∀uv∈E（G），有C（u）≠C（v），则f称为G的k－邻点可区别全染色.称

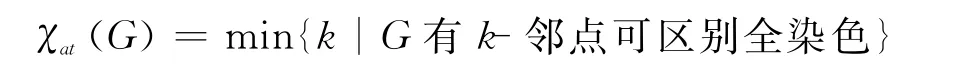
为G的邻点可区别全色数.

定义1.2［7］设G是阶至少为2的连通图，f是图G的使用颜色为1，2，…，k的全染色.如果G的任意相邻的点染不同的颜色，并且G的任意相邻的边染不同的颜色，那么称f为G的I－全染色.设f是G的I－全染色，对∀x∈V（G），令C（x）表示在f下点x的颜色及与x关联的全体边的颜色构成的集合，称之为在f下点x的色集合，令¯C（x）＝｛1，2，…，k｝＼C（x）.如果对∀uv∈E（G），有C（u）≠C（v），则f称为G的k－邻点可区别I－全染色（简记为k－AVDIT染色）.称

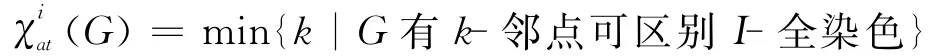
为G的邻点可区别I－全色数.

定义1.3 设k，m均为正整数，图Bk，m的定义如下：

定义1.4 设k，m均为正整数，且k≥3，图Rk，m的定义如下：

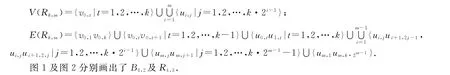
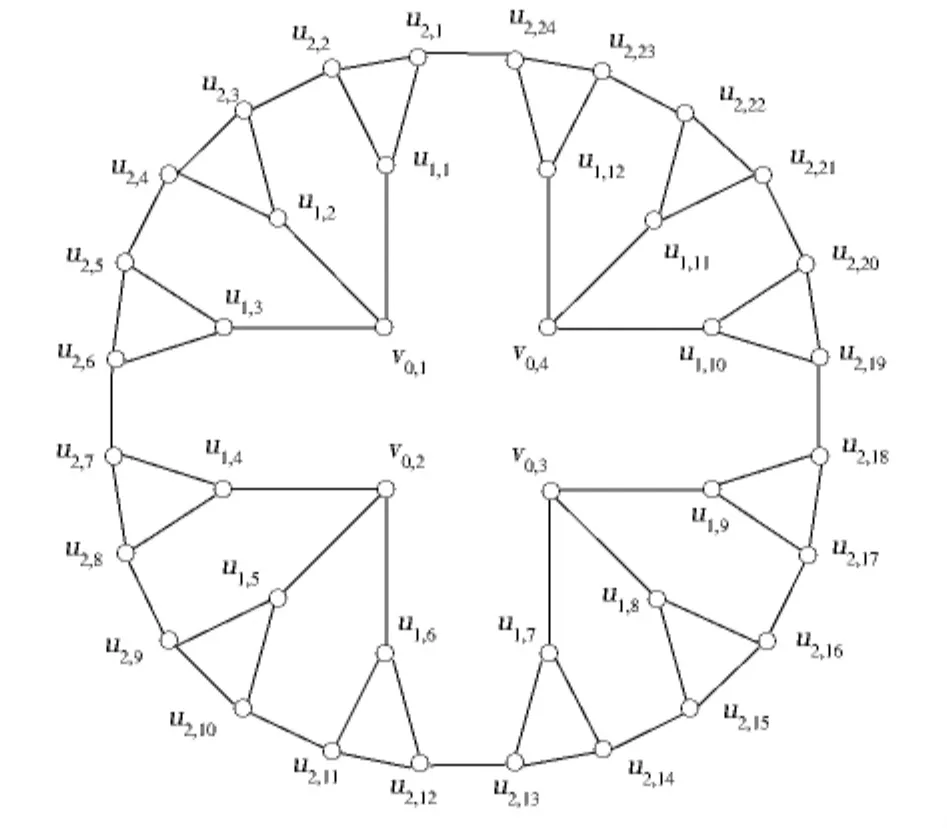
图1 B 4，2Fig.1 B 4，2

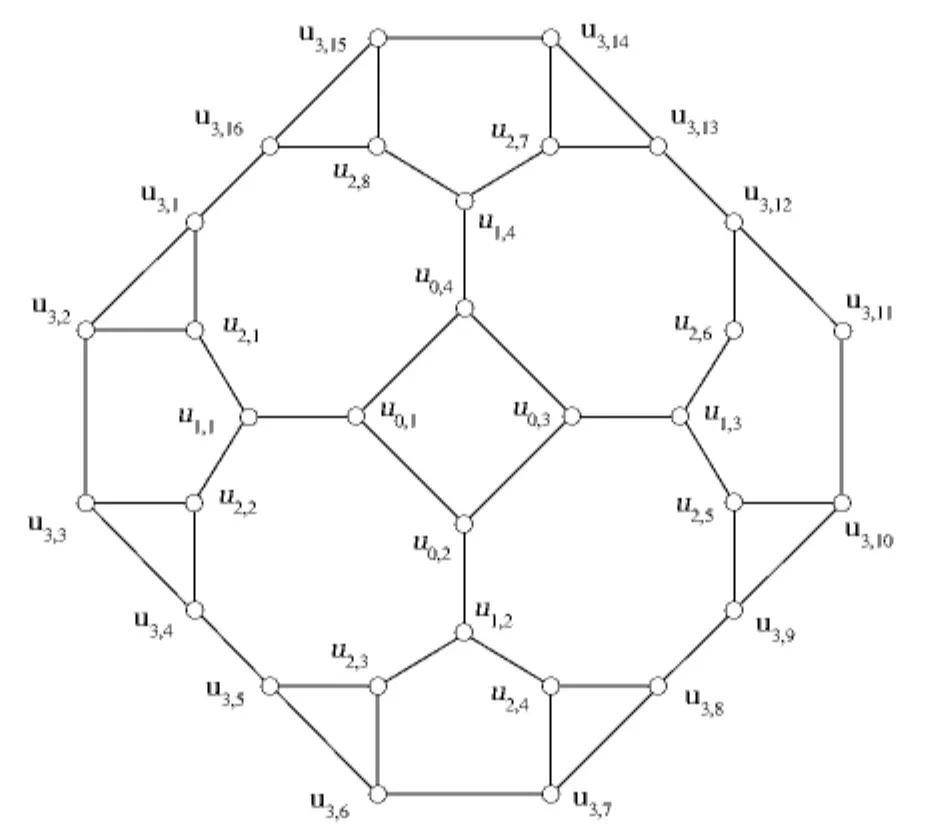
图2 R 4，3Fig.2 R4，3

本文给出了图Bk，m和R k，m的邻点可区别I－全色数.

在本文的主要定理的证明中，为了方便将“边ui，ju i＋1，2j－1和ui，ju i＋1，2j分别用颜色a和b去染色”写为“有序边对［ui，ju i＋1，2j－1，ui，ju i＋1，2j］用［a，b］去染”；

将“点ui＋1，2j－1和ui＋1，2j分别用颜色a和b去染色”写为“有序点对［ui＋1，2j－1，ui＋1，2j］用［a，b］去染”；对多于两条的边构成的有序组及多于两个的点构成的有序组，有类似的说法和记号.

图中未加说明的术语，记号可参看文献［8］.

1 主要结果

引理1.1［7］对简单图G，则有

（1）对∀x∈V（K4），都有｜¯C（x）｜＝1，由此可知，f（x）∈S（x）＝C（x），其中，S（x）表示在f下与x关联的全体边的颜色构成的集合，此时考虑f在E（K4）上的限制g，则g是K4的一个点可区别正常边染色，由参考文献［2］知χ′as（K4）＝5，显然矛盾.

（2）存在x∈V（K4），使得｜¯C（x）｜＝0，即C（x）＝｛1，2，3，4｝，不妨设C（v0.1）＝｛1，2，3，4｝且f（v0，1）＝1，则对于u1，1，u1，2，u1，3一定有｜C（u1，1）｜＝｜C（u1，2）｜＝｜C（u1，3）｜＝3，进而可知，f（u1，j）∈S（u1，j）＝C（u1，j）（j∈｛1，2，3｝）.

下面根据¯C（u1，1），¯C（u1，2），¯C（u1，3）三者中有没有等于｛1｝分两种情形讨论：

①若¯C（u1，1），¯C（u1，2），¯C（u1，3）三者中存在一个等于｛1｝，不妨设¯C（u1，1）＝｛1｝，即C（u1，1）＝｛2，3，4｝.若f（v0，1，u1，1）＝2，则边u1，1u1，2和u1，1u1，3只能分别用3，4或4，3去染，这就有C（u1，2）＝｛3，4，f（u1，2u1，3）｝，C（u1，3）＝｛3，4，f（u1，2u1，3）｝，由此可知，C（u1，2）＝C（u1，3）；对于f（u0，1u1，1）＝3或f（v0，1u1，1）＝4可得类似结果，这显然与f是K4的邻点可区别I－全染色矛盾.

②若¯C（u1，1），¯C（u1，2），¯C（u1，3）三者均不等于｛1｝，则¯C（u1，1），¯C（u1，2），¯C（u1，3）两两互不相等且只能分别取｛2｝，｛3｝，｛4｝中的某一个，此时，考虑f下在E（K4）上的即制g，则g是K4的一个点可区别正常边染色，又与χ′as（K4）＝5矛盾，综上所述可知，χi at（K4）＝χi

at（B1，1）＞4.

2）证明（B1，1）＝5.下面给出B1，1有一个5－AVDIT染色.定义一个从V（B1，1）∪E（B1，1）到｛1，2，3，4，5｝的映射f如下：f（v0，1）＝4，f（u1，j）＝j，f（v0，1u1，j）＝j，j∈｛1，2，3｝.f（u1，1u1，2）＝4，f（u1，2，u1，3）＝5，f（u1，1u1，3）＝2.在该染色下，有C（v0，1）＝｛1，2，3，4｝，C（u1，1）＝｛1，2，4｝，C（u1，2）＝｛2，4，5｝，C（u1，3）＝｛2，3，5｝.可看出，任意相邻两点的色集合不同.所以，f是3－正则图B1，1的一个5－AVDIT染色.

情形2 当k≥2且m＝1时，欲证明（Bk，1）＝4，仅需给出图Bk，1的一个4－AVDIT染色，如下构造Bk，1的一个使用颜色1，2，3，4的I－全染色f：

点v0，t（t∈｛1，2，…，k｝）用颜色2（当t≡1（mod2）时）或3（当t≡0（mod2）时）去染；

对于t∈｛1，2，…，k－1｝，有序三边组［v0，tu1，3t－2，v0，tu1，3t－1，v0，tu1，3t］和有序三点组［u1，3t－2，u1，3t－1，u1，3t］均用［4，1，3］（当t≡1（mod2）时）或［1，4，2］（当t≡0（mod2）时）去染；

有序三边组［v0，ku1，3k－2，v0，ku1，3k－1，u0，k u1，3k］和有序三点组［u1，3k－2，u1，3k－1，u1，3k］均用［4，3，1］（当k≡1（mod2）时）或［1，4，2］（当k≡0（mod2）时）去染；

对于t∈｛1，2，…，k－1｝，有序三边 组［u1，3t－2u1，3t－1，u1，3t－1u1，3t，u1，3t u1，3（t＋1）－2］均用［3，2，4］（当t≡1（mod2）时）或［2，3，1］（当t≡0（mod2）时）去染；

有序三边组［u1，3k－2u1，3k－1，u1，3k－1u1，3k，u1，3tu1，1］用［2，4，2］（当k≡1（mod2））或［2，3，1］（当k≡0（mod2）时）去染.

在上述染色下，C（v0，t）＝｛1，2，3，4｝，t∈｛1，2，…，k｝.

对于t∈｛2，…，k－1｝，当t≡1（mod2）时，C（u1，3t－2），C（u1，3t－1），C（u1，3t）分别为｛1，3，4｝，｛1，2，3｝，｛2，3，4｝；当t≡0（mod2）时，C（u1，3t－2），C（u1，3t－1），C（u1，3t）分别为｛1，2，4｝，｛2，3，4｝，｛1，2，3｝.

当k≡1（mod2）时，C（u1，1），C（u1，2），C（u1，3），C（u1，3k－2），C（u1，3k－1），C（u1，3k）分别为｛2，3，4｝，｛1，2，3｝｛2，3，4｝，｛1，2，4｝，｛2，3，4｝，｛1，2，4｝，

当k≡0（mod2）时，C（u1，1），C（u1，2），C（u1，3），C（u1，3k－2），C（u1，3k－1），C（u1，3k）分别为｛1，3，4｝，｛1，2，3｝，｛2，3，4｝，｛1，2，4｝，｛2，3，4｝，｛1，2，3｝.

可看出，任意相邻两点的色集合不同.所以，f是3－正则图B k，1的一个4－AVDIT染色.

情形3 当m≥2时，欲证明χi at（Bk，m）＝4，仅需给出图Bk，m的一个4－AVDIT染色.

在图Bk，m中与点v0，t的距离不超过m的所有点导出的子图记为∑t（t∈｛1，2，…，k｝），显然，∑t≅∑l（1≤t＜l≤k），该同构使得点v0，t与v0，l对应，点ui，j与u i，s对应，其中2i－1·3（t－1）＋1≤j≤2i－1·3t，2i－1·3（l－1）＋1≤s≤2i－1·3l且s－j＝2i－1·3（l－t）（i∈｛1，2，…，m｝），满足上述条件的∑t到∑l的同构是唯一的，因此，对于图Bk，m包含的每一个∑t（t∈｛1，2，…，k｝），利用前面所建立的同构关系可得∑t≅∑1（2≤t≤k），于是让∑t（t∈｛2，3，…，k｝）与∑1的染色相同（即∑t与∑1对应的边染同色，对应的点染同色），最后将未被染色的k条边均用1（若m≡0（mod2）时）或2（若m≡1（mod2）时）去染，这样得到Bk，m的一个染色记为f.

下面只需对∑1进行邻点可区别I－全染色，具体染色方法如下：

点v0，1用颜色2去染，

对有序三边组［v0，1u1，1，v0，1u1，2，v0，1u1，3］和有序点对［u1，1，u1，2，u1，3］均用［4，1，3］去染.

对于i∈｛1，2，…，m－1｝，j∈｛1，2，…，2i｝，有序边对［ui，ju i＋1，2j－1，ui，ju i＋1，2j］和有序点对［ui＋1，2j－1ui＋1，2j］均用［2，3］（若i≡1（mod2）时）或［1，4］（若i≡0（mod2）时）去染；

对于i∈｛1，2，…，m－1｝，j∈ ｛2i＋1，…，2i－1·3｝，有序边对 ［ui，j u i＋1，2j－1，ui，j u i＋1，2j］和 有 序点对［ui＋1，2j－1ui＋1，2j］均用［2，4］（若i≡1（mod2）时）或［1，3］（若i≡0（mod2）时）去染.

对于j∈｛1，2，…，2m｝且j≡1（mod2），有序边对［um，ju m，j＋1，um，j＋1um，j＋2］用［3，2］（若m≡1（mod2）时）或［4，1］（若m≡0（mod2））；

对于j∈｛2m＋1，…，2m－1·3｝且j≡1（mod2），有序边对［um，j u m，j＋1，um，j＋1um，j＋2］用［4，2］（若m≡1（mod2）时）或［3，1］（若m≡0（mod2）时）去染，最后将边um，3·2m－1um，3·2m－1＋1的色去掉.

下面只需说明∑1中任两个相邻点在f下的色集合不同.显然有C（v0，1）＝｛1，2，3，4｝，C（v1，1），C（u1，2），C（u1，3），分别为｛2，3，4｝，｛1，2，3｝，｛2，3，4｝，其余各点ui，j（i∈｛2，3，…，m｝）的色集合为

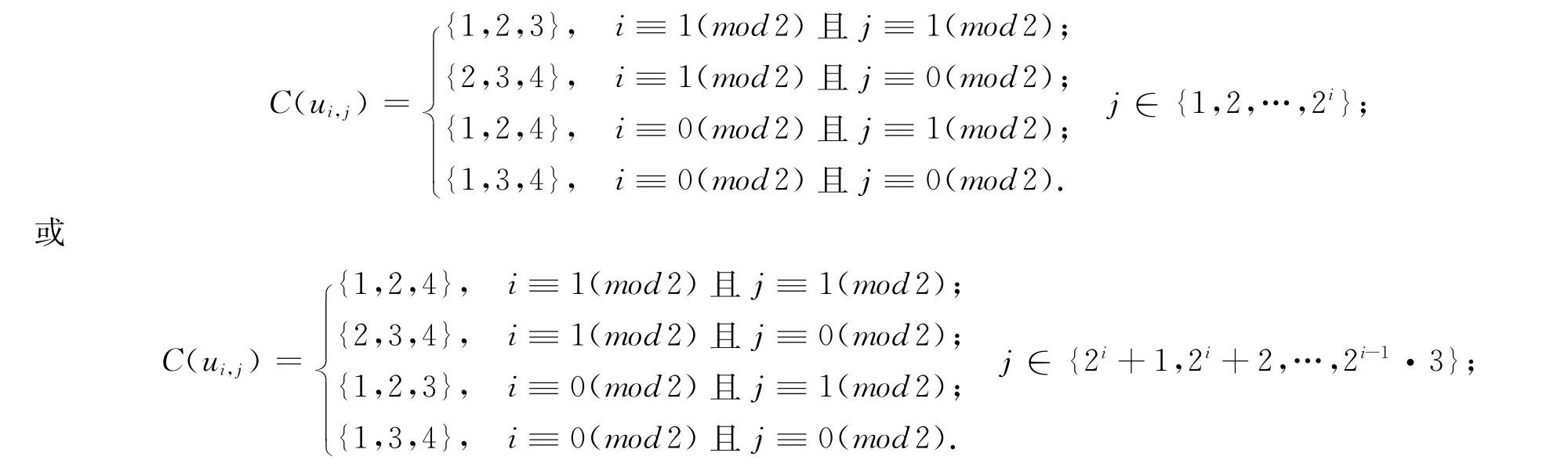
特别地，当m≡1（mod2）时，C（um，1）＝｛1，2，3｝，C（um，2m－1），C（um，2·2m－1），C（um，3·2m－1）均为｛2，3，4｝；当m≡0（mod2）时，C（um，1）＝｛1，2，4｝，C（um，2m－1），C（um，2·2m－1），C（um，3·2m－1）均为｛1，3，4｝，可看到，任意相邻两点的色集合不同.所以，f是3－正则图B k，m的一个4－AVDIT染色.

定理1.2 对于3－正则图R k，m，则有χi at（Rk，m）＝4.

证明 易知Δ（Rk，m）＝3，由引理1.1知，χi at（Rk，m）≥4，欲证明χiat（Rk，m）＝4，仅需给出图Rk，m的一个4－AVDIT染色的.下面分两种情形进行证明.

情形1 当m＝1时.

（1）当k＝3时，将3－正则图R3，1的染色方法记为R3染法，具体如下：

有序三边组［v0，1v0，2，v0，2v0，3，v0，3v0，1］和有序三点组［v0，1，v0，2，v0，3］均用［1，2，3］去染；

有序三边组［u1，1u1，2，u1，2u1，3，u1，3u1，1］和有序三点组［u1，1，u1，2，u1，3］均用［2，3，1］去染；剩余的边均用4去染.

在上述染色之下，

C（v0，1），C（v0，2），C（v0，3）分别为：｛1，3，4｝，｛1，2，4｝，｛2，3，4｝；

C（u1，1），C（u1，2），C（u1，3）分别为：｛1，2，4｝，｛2，3，4｝，｛1，3，4｝；可看到，任意相邻两点的色集合不同.所以，上述染色是3－正则图R3，1的一个4－AVDIT染色.

（2）当k＝4时，将3－正则图R4，1的染色方法记为R4染法，具体如下：

有序四边组［v0，1v0，2，v0，2v0，3，v0，3v0，4，v0，4v0，1］和有序四点组［v0，1，v0，2，v0，3，v0，4］均用［1，2，4，3］去染；

有序四边组［u1，1u1，2，u1，2u1，3，u1，3u1，4，u1，4u1，1］和有序四点组［u1，1，u1，2，u1，3，u1，4］均用［2，4，3，1］去染；

有序四边组［v0，1u1，1，v0，2u1，2，v0，3u1，3，v0，4u1，4］用［4，3，1，2］去染.

在上述染色之下，C（v0，1），C（v0，2），C（v0，3），C（v0，4）分 别 为 ｛1，3，4｝，｛1，2，3｝，｛1，2，4｝，｛2，3，4｝；C（u1，1），C（u1，2），C（u1，3），C（u1，4）分别为：｛1，2，4｝，｛2，3，4｝，｛1，3，4｝，｛1，2，3｝，可看到，任意相邻两点的色集合不同.所以，上述染色是3－正则图R4，1的一个4－AVDIT染色.

（3）当k＝5时，3－正则图R5，1的染色方法记为R5，具体如下：

有序五边组［v0，1v0，2，v0，2v0，3，v0，3v0，4，v0，4v0，5，v0，5v0，1］用［4，1，4，2，1］去染；

有序五点组［v0，1，v0，2，v0，3，v0，4，v0，5］用［4，3，4，3，1］去染.

有序五边组［u1，1u1，2，u1，2u1，3，u1，3u1，4，u1，4u1，5，u1，5u1，1］用［1，4，3，2，4］去染.

有序五点组［u1，1，u1，2，u1，3，u1，4，u1，5］用［3，4，2，1，4］去染；

有序五边组［v0，1u1，1，v0，2u1，2，v0，3u1，3，v0，4u1，4，v0，5u1，5］用［2，2，2，1，3］去染.

在上述染色之下，C（v0，1），C（v0，2），C（v0，3），C（v0，4），C（v0，5）分别为｛1，2，4｝，｛1，2，3，4｝，｛1，2，4｝，｛1，2，3，4｝，｛1，2，3｝；C（u1，1），C（u1，2），C（u1，3），C（u1，4），C（u1，5）分别为｛1，2，3，4｝，｛1，2，4｝，｛2，3，4｝，｛1，2，3｝，｛2，3，4｝，可看到，任意相邻两点的色集合不同.所以，上述染色是3－正则图R5，1的一个4－AVDIT染色.

（4）当k≥6时，对于3－正则图R k，1的染色可以将R3染法和R4染法作为工具反复使用，具体如下：

为了说明方法的合理性，我们仅对R4染法与R3染法一次结合验证，以R7，1为例.

先用一次R4染法：有序四边组［v0，1v0，2，v0，2v0，3，v0，3v0，4，v0，4v0，5］和有序四点组［v0，1，v0，2，v0，3，v0，4］均用［1，2，4，3］去染；有序四边组［u1，1u1，2，u1，2u1，3，u1，3u1，4，u1，4u1，5］和有序四点组［u1，1，u1，2，u1，3，u1，4］均用［2，4，3，1］去染；有序四边组［v0，1u1，1，v0，2u1，2，v0，3u1，3，u0，4v1，4］用［4，3，1，2］去染.

然后用一次R3染去：有序三边组［v0，5v0，6，v0，6v0，7，v0，7v0，1］和有序三点组［v0，5，v0，6，v0，7］均用［1，2，3］去染；有序三边组［u1，5u1，6，u1，6u1，7，u1，7u1，1］和有序三点组［u1，5，u1，6，u1，7］均用［2，3，1］去染；剩余的边均用4去染.

在上述染色之下，C（v0，1），C（v0，2），C（v0，3），C（v0，4），C（v0，5），C（v0，6），C（v0，7）分别为：｛1，2，4｝，｛2，3，4｝，｛1，3，4｝，｛1，2，4｝，｛2，3，4｝，；C（u1，1），C（u1，2），C（u1，3），C（u1，4），C（u1，5），C（U1，6），C（u1，7）分别为：｛1，2，4｝，｛2，3，4｝，｛1，3，4｝，｛1，2，3｝，｛1，2，4｝，｛2，3，4｝，｛1，3，4｝.可看到，任意相邻两点的色集合不同，说明对3－正则图R k，1的这种染色方法是合理的，进而说明上述染色是3－正则图R k，1的一个4－AVDIT染色.

情形2 当m≥2时.

在图Rk，m中与点v0t（此时暂不考虑v0，t与其它v0，l之间的边）的距离不超过m－1的所有点导出的子图记为∑t（t∈｛1，2，…，k｝），显然∑t≅∑p（1≤t＜p≤k），该同构使得点v0，t与v0，p对应，点ui，j与u i，s对应，其中2i－1·（t－1）＋1≤j≤2i－1·t，2i－1·（p－1）＋1≤s≤2i－1·p且s－j＝2i－1·（p－t）（i∈｛1，2，…，m｝）.满足上述条件的∑t到∑p的同构是唯一的，因此，对于图Rk，m包含的每一个∑t（t∈｛1，2，…，k｝），利用前面所建立的同构关系可得∑t≅∑p（1≤t＜p≤k），于是当t≡1（mod2）（t∈｛3，4，…，k－1｝）让∑t与∑1的染色相同（即∑t与∑2对应的边染同色，对应的点染同色）；当t≡0（mod2）（t∈｛3，4，…，k－1｝）让∑t与∑2的染色相同（即∑t与∑2对应的边染同色，对应的点染同色）；对∑k来说，当k≡0（mod2）时与∑2的染色相同，当k≡1（mod2）时，∑k的单独染色.

下面只需对∑1，∑2，∑k（若k≡1（mod2）时）进行邻点可区别I－全染色.

第一步，对∑1染色.

点v0，1用颜色1去染，边v0，1u1，1和点u1，1均用颜色4去染；

对于i∈｛1，2，…，m－1｝，j∈｛1，2，…，2i－1｝，有序边对［ui，j u i＋1，2j－1，ui，j u i＋1，2j］和有序点对［ui，1，2j－1，ui＋1，2j］均用［2，3］（若i≡1（mod2）时）或［1，4］（若i≡0（mod2）时）去染；

对于j∈｛1，2，…，2m－1｝且j≡1（mod2），有序边对［um，ju m，j＋1，um，j＋1um，j＋2］用［3，2］（若m≡1（mod2）时）或［4，1］（若m≡0（mod2）），最后将边um，2m－1um，2m－1＋1的色去掉.

特别地，当k≡1（mod2）且m＝2时，将点u2，1的颜色2换成颜色1.

第二步，对∑2染色.

点v0，2用颜色2去染，边v0，2u1，2和点u1，2均用颜色3去染；

对于i∈｛1，2，…，m－1｝，j∈｛2i－1＋1，…，2i－1·2｝，有序边对［ui，j u i＋1，2j－1，ui，j u i＋1，2j］和有序点对［ui＋1，2j－1，ui＋1，2j］均用［2，4］（若i≡1（mod2）时）或［1，3］（若i≡0（mod2）时）去染；

对于j∈｛2m－1＋1，…，2m－1·2｝且j≡1（mod2），有序边对［um，j u m，j＋1，um，j＋1um，j＋2］用［4，2］（若m≡1（mod2）时）或［3，1］（若m≡0（mod2）），最后将边um，2·2m－1um，2·2m－1＋1的色去掉.

第三步，对∑k（当k≡1（mod2）时）染色.

点v0，k用颜色3去染，边v0，ku1，k和点u1，k均用颜色4去染；

对于i∈｛1，2，…，m－1｝，j∈｛2i－1·（k－1）＋1，…，2i－1·k｝，有序边对［ui，ju i＋1，2j－1，ui，ju i＋1，2j］和有序点对［ui＋1，2j－1，ui＋1，2j］均用［2，1］（若i≡1（mod2）时）或［3，4］（若i≡0（mod2）时）去染；

对于j∈｛（k－1）·2m－1＋1，…，k·2m－1｝且j≡1（mod2），有序边对［um，ju m，j＋1，um，j＋1um，j＋2］用［1，2］（若m≡1（mod2）时）或［4，3］（若m≡0（mod2）），最后将边um，k·2m－1um，1的色去掉.

特别地，当m＝2时，将点u1，k的颜色4换成颜色2，将点u2，2k－1的颜色2换成颜色3，将点u2，2k的颜色1换成颜色4；当m≡1（mod2）（m≥3）时，将点um，（k－1）·2m－1＋1的颜色3换成颜色1.

对边v0，tv0，t＋1（t∈｛1，2，3，…，k－1｝）用颜色1（当t≡1（mod2）时）或2（当t≡0（mod2）时）去染；

对边v0，kv0，1用颜色3（当k≡1（mod2）时）或2（当k≡0（mod2）时）去染；

最后将未被染色的k条边均用2（若m≡1（mod2）时）或1（若m≡0（mod2）时）去染，特别地，当k≡1（mod2）且m≡0（mod2）时，将边um，k·2m－1um，1的色换成3，将图Rk，m的这一个染色记为f.

下面只需说明∑1，∑2，∑k（当k≡1（mod2）时）中任两个相邻点在f下的色集合不同，

在上述染色下，有

特别地，当m＝2时C（u2，2k－1）＝｛1，2，3，4｝；当m≡0（mod2）（m≥3）时C（um，（k－1）·2m－1＋1＝｛1，2，4｝.可看出，任意相邻两点的色集合不同，所以，上述染色f是3－正则图R k，m的一个4－AVDIT染色.

［1］ Fravaron O，Li H，Schelp R H.Strong Edge Colorings of Graphs［J］.DiscreteMathematics，1996，159（1－3）：103－109.

［2］ Zhang Zhong－fu，Liu Lin－zhong，Wang Jian－fang.Adjacent Strong Edge Coloring of Graphs［J］.AppliedMathematicaLetters，2002，15：623－626.

［3］ Cheng Xiang－en，Zhang Zhong－fu，Yan Jing－zhi，etal.Adjacent－vertex－Distinguishing Total Chromatics Numbers onM ycielski’sGraphs of Several Kinds of Particular Graphs［J］.JournalofLanzhouuniversity（NaturalScience），2005，41（2）：117－122.

［4］ 陈祥恩.关于图r K2∨Ks的邻点可区别全色数［J］.兰州大学学报：自然科学版，2007，43（5）：91－93.

［5］ 陈祥恩，张忠辅.关于图K2n＋1－E（2K2）的邻点可区别全色数［J］.兰州大学学报：自然科学版，2005，41（6）：102－105.

［6］ 杨随义，王治文.一类3－正则图的关联邻点可区别全染色［J］.山西大学学报：自然科学版，2010，33（3）：354－357.

［7］ Zhang Zhong－fu，Woodall D R，Yao Bing，etal.Adjacent Vertex－distinguishing I－total Coloring of Graphs［EB／OL］.（2008－06－12）http：／／202.201／18.40：8080／mas5／.

［8］ Bondy J A，Murty U S R.Graph Theory［M］.London：Springer，2008.

Adjacent Vertex－distinguishing I－total Coloring of Two Kinds of 3－regular Graphs

YANG Sui－yi，YANG Xiao－ya，TANG Bao－xiang，HE Wan－sheng
（DepartmentofMathematics，TianshuiNormalUniversity，Tianshui741001，China）

The I－total coloring of a graphsGis an assignment of some colors to its vertices and edges such that no two adjacent vertices receive the dame color and no two adjacent edges receive the same color.Under the I－total coloring ofG，the color set of a vertexxofGis the set of all colors which are assigned to vertexxor the edges incident tox.An I－total coloring is called adjacent vertex distinguishing if any two adjacent vertices have different color sets.The minimum number of colors required in an adjacent vertex－distinguishing I－total coloring is called adjacent vertex－distinguishing I－total chromatic number.The adjacent vertex－distinguishing I－total coloring of two kind of 3－regular graphs are discussed.

I－total coloring；adjacent vertex－distinguishing I－total coloring；adjacent vertexdistinguishing I－total chromatic number

O157.5

A

2011－04－19；

2011－06－10

甘肃省自然科学基金（096RJZE106）；天水师范学院中青年教师科研资助项目（TSA1102）

杨随义（1977－），男，甘肃天水人，硕士，副教授，研究方向：代数图论与染色.E－mail：yangzhangyike＠yahoo.com.cn

0253－2395（2012）04－0641－07

book=647,ebook=349