＊ 一类正线性映射的可分解性和最优性

侯晋川，李丽君

（1.太原理工大学 数学学院，山西 太原 030024；2.山西大学 数学与应用数学研究所，山西 太原 030006）

＊一类正线性映射的可分解性和最优性

侯晋川1，2，李丽君1

（1.太原理工大学 数学学院，山西 太原 030024；2.山西大学 数学与应用数学研究所，山西 太原 030006）

非完全正的正线性映射在判定复合系统量子态的纠缠性中起关键作用.文章研究一类非完全正的正线性映射的性质，证明了此类正线性映射Φ是可分解的，不是2－正的，并给出了由此类正线性映射Φ生成的纠缠witnessesWΦ成为最优的充分必要条件.

正映射；可分解性；最优性

0 引言

在量子力学、量子计算和量子信息理论中，量子纠缠态一直被看做量子信息处理和通信中最基本的资源.因此，寻找检测量子纠缠性的方法是该领域重要而具有挑战性的基本问题.目前已经找到一些检测量子纠缠性的判据，例如正映射判据，纠缠witness判据，PPT判据，重排判据（参见［1－6］）等等.正线性映射和完全正线性映射在量子信息理论中发挥着重要的作用.一个量子态是否是纠缠态可以用非完全正的（简单记作NCP）正线性映射来检测，而量子信道都可以用保迹的完全正的线性映射来表示.

量子态可以表示为复Hilbert空间上迹为1的正算子（半正定矩阵）.设H，K是复Hilbert空间，复合系统H⊗K上的态ρ是纠缠的如果它不能表示为形如∑n i＝1p iρi⊗σi的态的（迹范数）极限，这里ρi，σi分别为H，K上的态，数p i＞0且∑ip i＝1.在众多的纠缠判据当中，正映射判据和纠缠witness判据［1，3－4］给出了量子态纠缠的充分必要条件.一个给定的量子态是纠缠的当且仅当至少存在一个NCP正线性映射（纠缠witness）能够检测它.因此探讨NCP正线性映射和纠缠witness的性质并尽可能多地掌握NCP正线性映射和纠缠witness的例子是很重要的.

注意，当dimH⊗K＜∞时，由 Choi－Jamiolkowski同构［7－8］，对于事先任意取定的一组基｛｜i〉｝，每一个NCP正线性映射Φ∶B（H）→B（K）对应一个作用在H⊗K上的纠缠witnessWΦ＝（Φ（Eij）），其中E ij＝｜i〉〈j｜表示（i，j）元为1其它元为0的矩阵，我们称这个矩阵为Choi－Jamiolkowski矩阵.此时我们说WΦ是NCP正映射Φ对应的纠缠witness.反过来，对于一个纠缠witnessW来说，我们用ΦW来表示这个纠缠witness所对应的正映射，因此，W＝WΦW（参见［4，9－11］）.

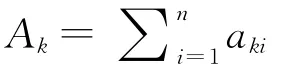
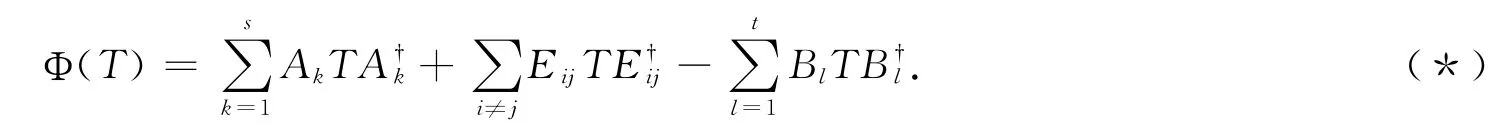
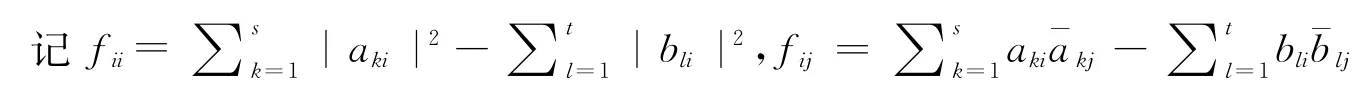
1 预备知识

下面介绍本文中用到的一些基本的知识.

设Φ∶B（H）→B（K）是线性映射.如果对于任意的A∈B（H），A是正的蕴含Φ（A）也是正的，那么我们就称Φ是正的；如果有Φn＝Φ⊗In是正的，那么我们就说Φ是n－正的；如果对任意的n＞0，Φn都是正的，那么我们就说Φ是完全正的.正映射判据断言：如果ρ是H⊗K上的纠缠态，则存在NCP正映射Φ∶B（H）→B（K）使得（Φ⊗I K）ρ不是正算子.

纠缠witness（或者简称witness）W是作用在H⊗K（H，K是两个可分的复Hilbert空间）上的自伴算子（也称为Hermitian算子）并且满足对所有的可分态σ有Tr（Wσ）≥0，并且至少存在一个纠缠态ρ使得Tr（Wρ）＜0（在这种情况下，我们就说W可以检测ρ，或者说W是ρ的一个witness）［12］.而纠缠witness判据则说任何一个纠缠态都可以被某个特殊的witness检测.

但是注意不存在这样的NCP正映射和纠缠witness可以检测所有纠缠态.对于任意的两个纠缠witnessesW1和W2，如果W1比W2检测的纠缠态多，那么我们就说W1比W2更优.刻画witness的一个特别重要的特性就是最优性的概念.大致说来，最优的witness就是能够检测最多的纠缠态的witness.也就是说，如果不存在其他的witness比W更优，我们就说witnessW是最优的.

如果一个纠缠witness可以表示成W＝P＋QΓ的形式，那么，就称W是可分解的，其中P≥0，Q≥0，QΓ表示QT1和QT2中的任意一个，而QT1和QT2又分别表示Q根据子系统H和K的部分转置.如果一个给定的witness不能写成这种形式，我们就说这个纠缠witness是不可分解的.类似地，如果一个正映射Φ可以写成一个完全正映射Φ1加上一个完全正映射Φ2和转置T复合的形式，即Φ＝Φ1＋T◦Φ2，那么我们就称这个正映射是可分解的.WΦ是可分解的当且仅当Φ是可分解的.

命题1.1［13］W是最优的纠缠witness当且仅当对当任意的正算子Q，W－Q不再是纠缠witness.

命题1.2［13］如果集合PW＝｛｜ψ〉｜φ〉∈H⊗K∶〈ψ｜〈φ｜W｜ψ〉｜φ〉＝0｝能够张成整个空间H⊗K，那么W就是最优的（在这种情况下，我们就说W具有张性质）.

注意命题1.2仅仅是个充分条件，已经找到不具备张性质的最优的witness.例如，Choi映射φ∶M3→M3生成的纠缠witnessWφ是最优的，其中φ的定义为

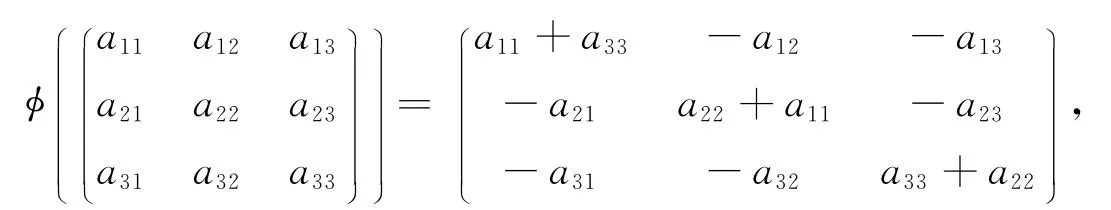
但是集合PWφ并不能张成整个空间C3⊗C3.

2 主要结果及证明

下面是本文的一些主要结果.

定理2.1 式（＊）中构造的正线性映射Φ是可分解的.

证明 注意到

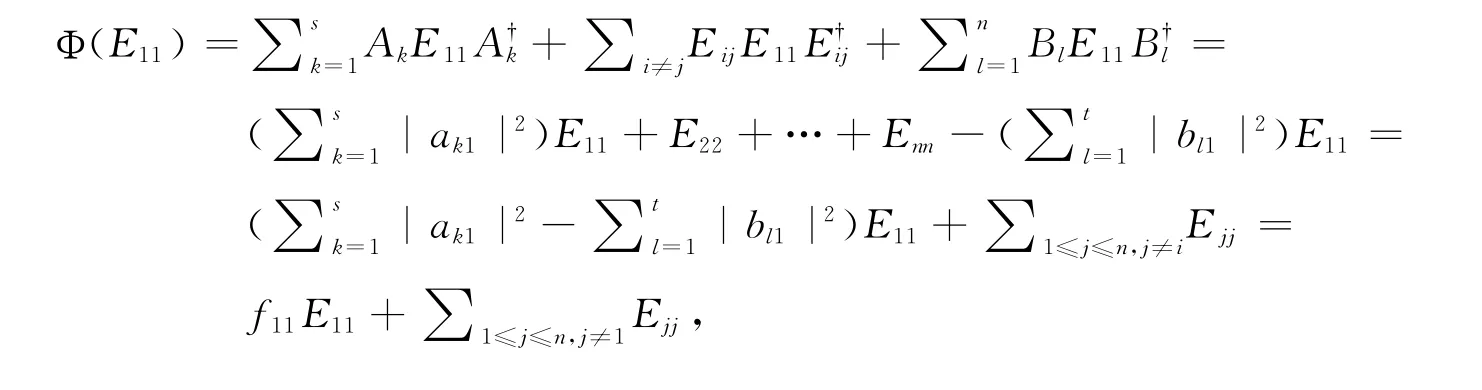
.由于｜x〉是任意的，这个等式不能总成立.所以，Φ不是2－正的.证毕.

下面考虑这类纠缠witness的最优性问题.我们得到WΦ最优的一个充分必要条件，即，

定理2.3 设Φ为式（＊）中的正线性映射.那么，纠缠witnessWΦ是最优的当且仅当∀i，f ii＝0且∀i≠j，｜f ij｜＝1.

证明 必要性.我们只需证明以下两个部分：（i）如果存在某个i使得f ii＞0，那么WΦ不是最优的；（ii）如果对于任意的i，f ii＝0并且存在某对i，j使得｜f ij｜＜1，那么WΦ不是最优的.我们分别给出它们的证明.首先，如果存在某个i使得f ii＞0，那么我们就有

这样，我们就证明了D＝0.因此，当n＝3时，W是最优的.

我们在这里指出，文献［14］中也得到定理2.3中的“充分性”部分.但我们这里用到的证明方法与文献［14］中的方法是不一样的.为了证明纠缠witnessWΦ是最优的，文献［14］应用的是命题1.2，即张性质，而我们用的是命题1.1.

［1］ Hou Jin－chuan.A Characterization of Positive Linear Maps and Criteria for Entangled Quantum States［J］.JPhysA：MathTheor，2010（43）：385201；ar Xiv［quant－ph］：1007.0560v1.

［2］ Hou Jin－chuan，Qi Xiao－fei.Constructing Entanglement Witnesses for Infinite－dimensional Systems［J］.PhysRevA，2010（81）：062351；ar Xiv：1005.5530v2.

［3］ Qi Xiao－fei，Hou Jin－chuan.Positive Finite Rank Elementary Operators and Characterizing Entanglement of States［J］.J PhysA：MathTheor，2011，44：215305.

［4］ Horodecki M，Horodecki P，Horodecki R.Separability of Mixed States：Necessary and Sufficient Conditions［J］.PhyLettA，1996，223：1－8.

［5］ Peres A.Separability Criterion for Density Matrices［J］.PhysLettA，1996，202：16.

［6］ Chen K，Wu L A.A Matrix Realignment Method for Recognizing Entanglement［J］.QuantInfComput，2003，3：193.

［7］ Choi M D.Completely Positive Linear Maps on Complex Matrices［J］.LinAlgAppl，1975（10）：285－290.

［8］ Jamiolkowski A.Linear Transformations which Preserve trace and Positive Semi definiteness of Operators［J］.RepMath Phys，1972，3：275.

［9］ Augusiak R，Stasi’nska J.General Scheme for Construction of Scalar Separability Criteria from Positive Maps［J］.Phy RevA，2008，77：010303.

［10］ Chrus′cin′ski D，Kossakowski A.On the Structure of Entanglement Witnesses and New Class of Positive Indecomposable Maps［J］.OpenSystemsandInf.Dynamics，2007，14：275.

［11］ Chrus′cin′ski D，Kossakowski A.A Class of Positive Atomic Maps［J］.JPhysA：MathTheor，2008，41：215201.

［12］ Hou Jin－chuan，Guo Yu.When Different Entanglement Witnesses Detect the same Entangled Ststes Phys［J］.RevA，2010（82）：052301.

［13］ Lewensetein M，Kraus B，Cirac J I，etal.Optimization of Entanglement Witnesses［J］.PhysRevA，2000，62：052310.

［14］ Dariusz Chrus′cin′ski.Justyna Pytel Optimal Entanglement Witnesses from Generalized Reduction and Robertson Maps［J］.JPhysA：MathTheor，2011（44）：165304.

Decomposability and Optimality of a Class of Positive Maps

HOU Jin－chuan1，2，LI Li－jun1
（1.DepartmentofMathematics，TaiyuanUniversityofTechnology，Taiyuan030024，China；2.ResearchInstituteofMathematicsandAppliedMathematics，ShanxiUniversity，Taiyuan030006，China）

NCP positive linear maps play important rules in detecting entanglement of states in composite quantum systems.A kind of NCP positive maps are studied.It is shown that these positive linear mapsΦare decomposable and not 2－positive.A necessary and sufficient condition is given for the entanglement witnessesWΦarising from suchΦto be optimal.

positive map；decomposablity；optimality

O179；O413.1

A

0253－2395（2012）02－0181－07＊

2012－01－08；

2012－01－14

国家自然科学基金（11171249）

侯晋川（1954－），男，山西汾西人，理学博士，教授，研究领域为算子理论和算子代数、矩阵分析、线性系统、量子信息.E－mail：jinchuanhou＠yahoo.com.cn