利用一维正则化反演进行大地电磁测深数据拟二维反演解释
2012-01-11戴亦军童孝忠张连伟曹创华
戴亦军,童孝忠,张连伟,曹创华
(1.中南大学 信息物理工程学院,长沙 410083;2.铁道第三勘察设计院,天津 300251)
利用一维正则化反演进行大地电磁测深数据拟二维反演解释
戴亦军1,童孝忠1,张连伟2,曹创华1
(1.中南大学 信息物理工程学院,长沙 410083;2.铁道第三勘察设计院,天津 300251)
大地电磁测深的反演问题是不适定的,其反演结果不稳定,且具有非唯一性。通过在目标函数中采用正则化方法,可以使得不适定反演问题具有稳定的反演结果,并改善解的稳定性和非唯一性问题。为了提高野外大地电磁测深数据的处理效率和初步解释的精度,提出了大地电磁测深数据的一维正则化反演进行拟二维反演解释方法。这里所述的大地电磁测深一维反演解释,与以往的解释方法不同,其思路首先用Bostick反演的深度来控制层参数,使反演计算的模型参数仅存在电阻率;最后采用阻尼高斯-牛顿算法进行反演计算,并将Bostick反演结果作为反演计算的初始模型。通过模型试算,结果表明其处理速度快、解释直观,对野外大地电磁测深数据进行初步反演解释是可行的。
大地电磁测深;反演;正则化方法;阻尼高斯~牛顿算法
0 前言
大地电磁测深法(MT)是前苏联学者Tikhonov[1]和 Cagniard[2]于上世纪五十年代提出来的,是利用天然交变电磁场研究地球电性结构的一种地球物理勘探方法。由于它不用人工供电,成本低,工作方便,不受高阻层屏蔽,对低阻层分辨率高,且勘探深度仅与电磁场的频率有关,浅可达几十米,深可达数百公里,因此在许多领域内得到了广泛的应用。MT资料反演解释就是根据地表测得的地球电磁场响应,如视电阻率、阻抗相位、表面阻抗、倾子等,通过一定的优化处理求得一个合理的地电模型[3]。目前二维数据处理技术日趋成熟,比较典型的二维反演解释方法有:OCCAM法[4]、RRI法[5]、REBOCC 法[6]、NLCG 法[7]和 ABIC法[8]。同时,一维反演方法也很多,应用广泛的有:OCCAM反演[9]、一维连续介质反演的曲线对比法[10]、“正演修正法”一维反演[11]、二次函数逼近非线性反演[12]和自适应正则化反演[13]。
另外,一维反演通常是二维反演计算的第一步骤,并且可以采用一维反演方法对地质模型进行拟二维反演解释,往往能对MT数据解释带来有用的效果。拟二维反演方法的精度比不上二维反演[14],但由于其反演速度快、内存需求少,所以在实际工作中,可以对野外大地电磁测深数据进行初步解释。因此,使用一维反演方法进行拟二维反演解释还是非常有意义的。
作者在本文采用Bostick反演的深度来控制层参数,使反演计算的模型参数仅存在电阻率,并将Bostick反演结果作为反演计算的初始模型。
1 MT一维正演
假定地电剖面是水平分层均匀的,如果地电剖面共有N层,则共有2 N-1个参数,hi(i=1,2,…,N-1)和ρi(i=1,2,…,N)分别代表第i层的厚度和电阻率。
对于上述的一维层状介质模型,计算视电阻率ρa和相位φa的公式如式(1)。
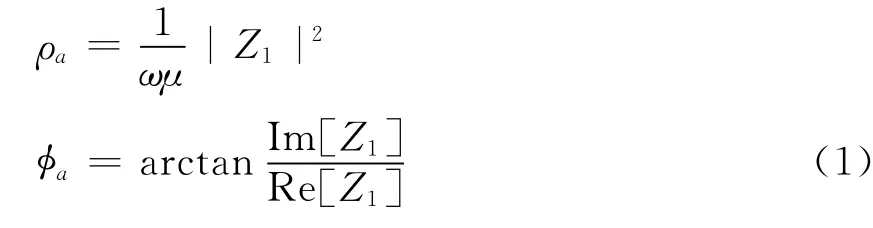
其中 Z1表示第一层地表的波阻抗;μ为导磁率;为角频率;Z可用下面的递推公式计算。1
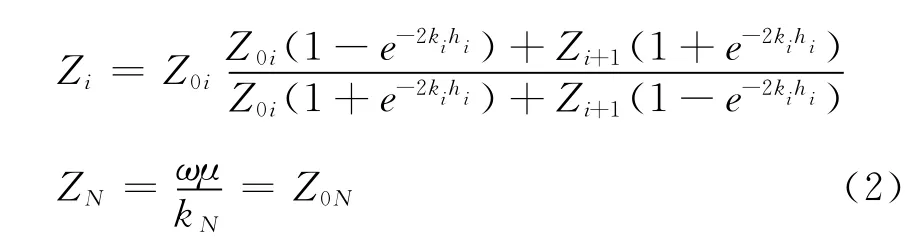
0ii层的特征阻抗;Zi是第i层顶面的波阻抗。
由此可见,对N层地电断面而言,若固定每一层的厚度,则视电阻率ρa和相位φa可表示为关于信号周期及层电阻率参数之间的函数,即
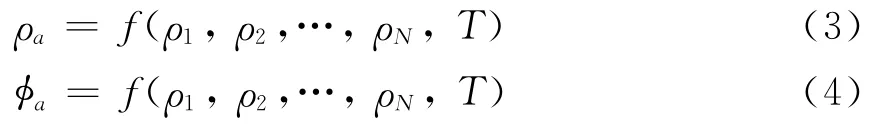
2 MT拟二维反演
2.1 反演问题描述
大地电磁反演问题,可以抽象地描述为已知观测数据求之于对应模型的过程。设d是观测数据向量,m是模型参数向量,F为把地球模型映射到理想数据的函数,则

式中 F为正演函数。
大地电磁反演问题是不适定的,其反演结果是不稳定的,并且具有非唯一性,这也就意味着不同的地电模型对观测数据的拟合具有同样的精度。在地球物理反演中,为了改善解的稳定性和非唯一性问题,通常是引入Tikhonov的正则化思想[15、16],见式(6)。
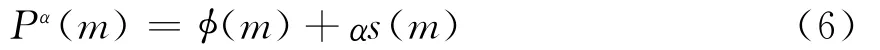
其中 Pα(m)为总目标函数;α为正则化因子;φ(m)为观测数据与预测数据之差的平方和(即数据目标函数);s(m)为稳定器(即模型约束目标函数),这里采用基于先验模型的最小模型约束。
因此,大地电磁反演问题的总目标函数表示为式(7)。
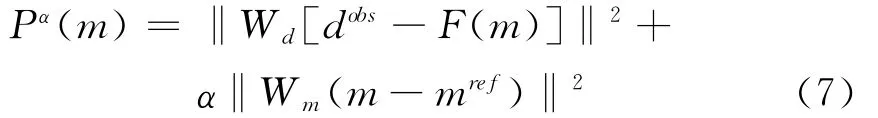
式中 Wd为数据权系数矩阵;Wm为模型权系数矩阵;mref为先验模型。
将F(m)用泰勒公式展开为式(8)。
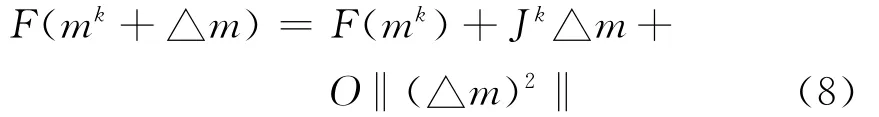
其中 mk为模型的第k次迭代值。

于是可得:这里 dk=F(mk);△m=mk+1-mk;Jk是雅克比灵敏度矩阵。
于是有:
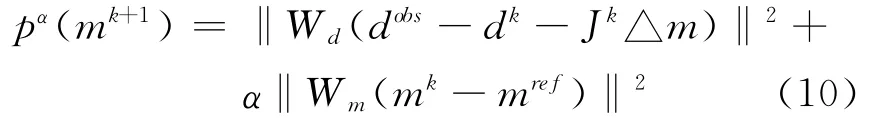
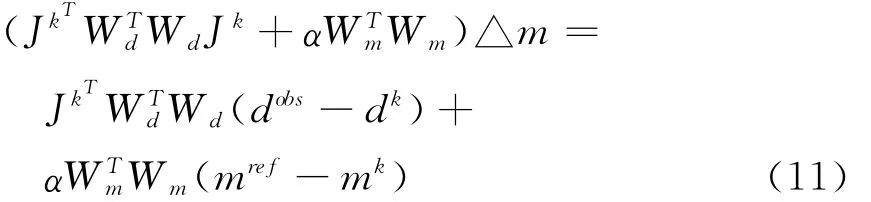
2.2 拟二维反演实现
对实测数据进行Bostick反演,求取地电模型的层厚度,并且使其在整个反演过程中保持不变,使反演计算的模型参数仅存在电阻率。这样层厚度参数不参与反演计算,即可实现一维正则化自动迭代反演计算。
线性方程组(11)求解采用阻尼~高斯牛顿算法,并将Bostick反演的电阻率作为反演计算的初始模型参数,将同一断面的多条MT测深曲线进行一维自动迭代反演,并把反演结果绘制成拟断面图,对其进行二维地质推断解释。
2.2.1 灵敏度矩阵的计算方法
在解决参数反演问题中的难点之一,就是计算观测数据关于模型参数的偏导数,即灵敏度矩阵,它们反映了参数的相对变化对观测数据相对变化的影响情况。同时它们还在模型参数与正演模拟响应之间,建立起一种线性关系。这里,我们采用扰动法来计算灵敏度矩阵,即利用一阶有限差分公式[17](12)来近似计算它们关于第k个参数 △mk的扰动,并通过正演问题来活动扰动后的大地电磁响应。
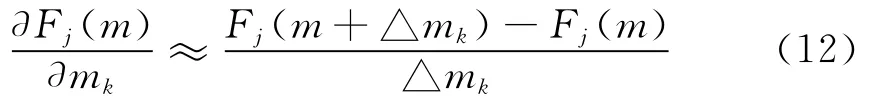
2.2.2 正则化因子的选取
在总目标函数中,正则化因子α为数据目标函数与模型约束目标函数的权重系数,它的大小决定了反演的拟合对象;α过大主要拟合先验模型,α过小则主要拟合观测数据。因此,正则化反演问题的关键,在于正则化因子的选取方法。在这里,我们采用广义交叉验证方法(Generalized Cross Validation,GCV)[18]来选取正则化因子,其正则化因子α的广义交叉验证函数可以写为式(13)。
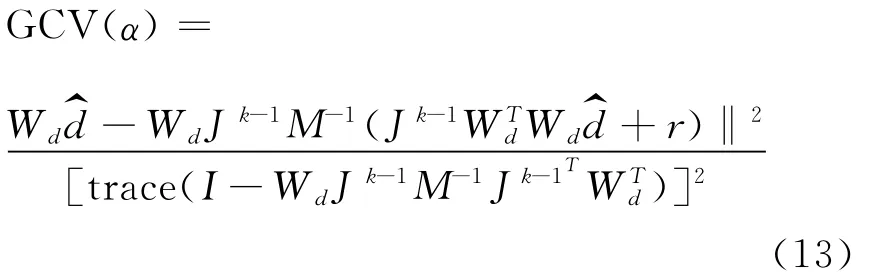
其中
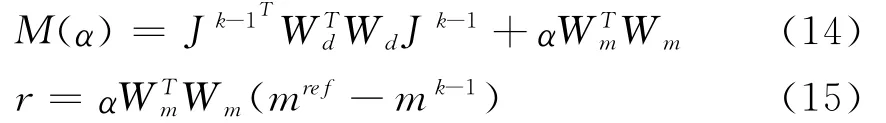
利用广义交叉验证方法,确定“最优”的正则化因子α,也就是寻找使GCV(α)函数达到极小时的α值。但该方法有时并不像我们想象的那样理想,在许多实际问题中,GCV函数在达到极小点时过于平坦,难于确定哪一点为最小值点。于是,我们采用类似离差原理的选取方法,将第k次迭代的正则化因子表示为式(16)。
αk= max(cαk-1,α*) (16)其中 0.01≤c≤0.5;α*为GCV函数的最小值。
3 算例
3.1 一维模型反演
选用K型地电模型正演理论数据进行反演计算,其真实的模型参数为:
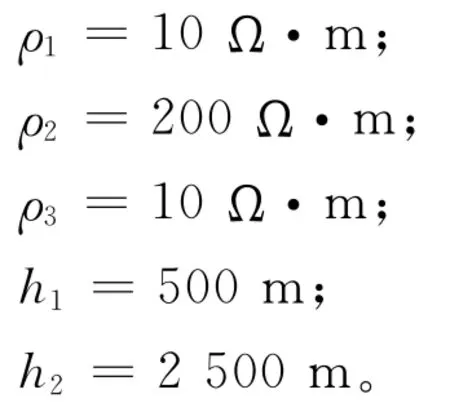
在反演计算中,将Bostick反演结果作为初始模型,先验模型取mref=0Ω·m,数据权系数矩阵取为单位矩阵,迭代次数为十次,图1和图2(见下页)显示了反演结果。
从图1可以看出,反演结果与实际的地电模型吻合较好。相对于Bostick反演,一维反演的结果更加准确地反映出中间高阻层的位置及大小。
从数据的拟合角度(见下页图2)看,一维反演的结果对理论数据的拟合非常好,也优于Bostick反演的拟合曲线。
3.2 二维模型反演
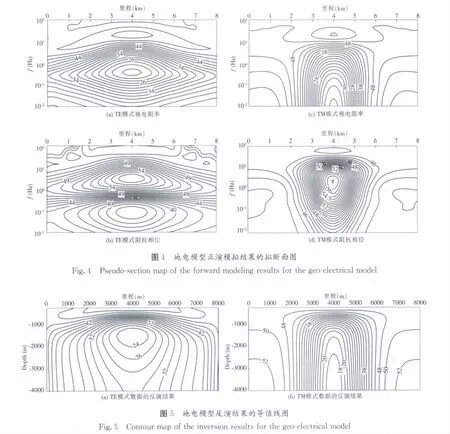
构造的地电模型如下页图3所示。在电阻率为50Ω·m的围岩中,存在电阻率为5Ω·m的低阻异常体,异常体顶部埋深1 000m。采用双二次插值的有限单元法进行正演计算[19],模拟测点数为25个,采用40个记录频点(0.01Hz~100Hz),并绘制出视电阻率和阻抗相位拟断面图(如下页图4所示)。
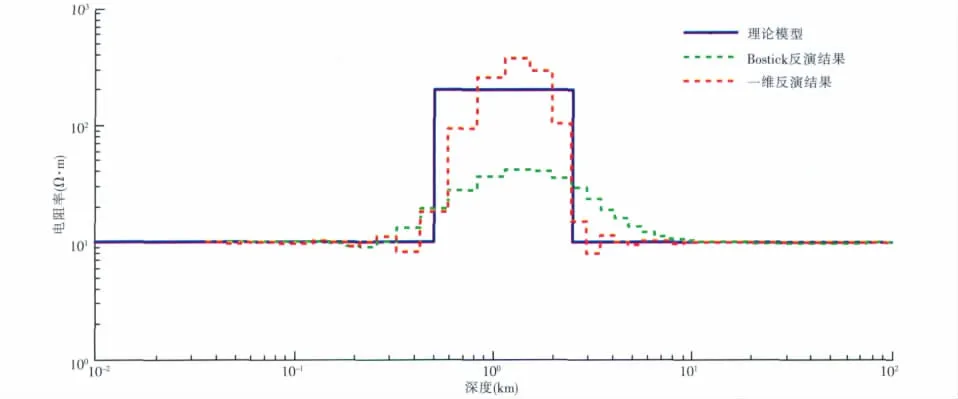
图1 三层地电模型的真实结果与反演结果对比图Fig.1 Comparison of the true and inversion results of three-layer geo-electrical model
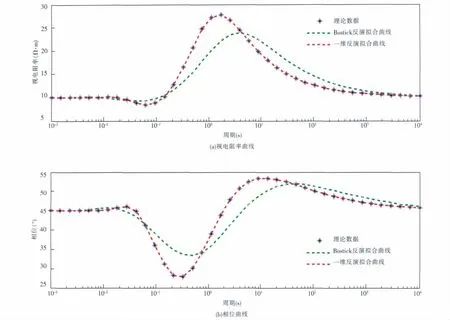
图2 大地电磁响应的真实结果与反演结果对比图Fig.2 Comparison of the true and inversion results of MT response
作者在对地电模型正演产生的TE模式数据和TM模式数据进行了一维反演,并绘制出视电阻率拟二维反演等值线图(见下页图5)。可以看出,虽然反演的电阻率参数值还存在较大误差,但异常体的形态还是得到了较好的反映。
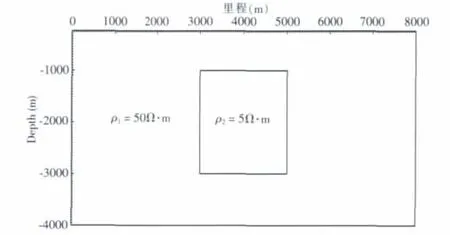
图3 地电模型Fig.3 The geo-electrical model
4 结论
(1)大地电磁测深反演问题是不适定的,其反演结果是不稳定的,并且具有非唯一性。这也就意味着不同的地电模型,对观测数据的拟合具有同样的精度。在目标函数中采用正则化方法,可以使得不适定反演问题,具有稳定的反演结果,改善了解的稳定性和非唯一性问题。
(2)与传统的一维大地电磁测深反演方法相比,由于将Bostick反演结果作为反演计算的初始模型,因此不需要人工输入初始模型参数,从而提高了工作效率。
(3)虽然拟二维反演方法的精度比不上二维反演,但由于其反演速度快、内存需求少,所以在实际工作中,可以对野外大地电磁测深数据进行初步解释。
[1] TIKNONOV A N.On determining electrical charac-teristics of the deep layers of the earth’s crust[J].Deki Akud Nuck,1950(73):295.
[2] CAGNIARD L.Basic theory of the magnetotelluric methods of geophysicalprospecting[J].Geophysics,1953(18):605.
[3] 陈乐寿,刘任,王天生.大地电磁测深资料处理与解释[M].北京:石油工业出版社,1989.
[4] DEGROOT-HEDLIN C,CONSTABLE S.Occam’s inversion to generate smooth,two-dimensional models from magnetotelluric data[J].Geophysics,1990,55(12):1613.
[5] 高才坤,汤井田,王烨,等.基于RRI反演的高频大地电磁测深在深边部矿产勘探中的试验研究[J].地球物理学进展,2009,24(1):309.
[6] SIRIPUNVARAPORN W,EGBERT G.An efficient data-subspace inversion method for 2-D magnetotelluric data[J].Geophysics,2000,65(3):791.
[7] RODI W,MACKIE R L.Nonlinear conjugate gradient algorithm for 2-D magnetotelluric inversion[J].Geophysics,2001,66(1):174.
[8] UCHIDA T.Smooth 2-D inversion for magnetotelluric for magnetotelluric data based on statistical criterion ABIC[J].Journal of Geomagnetism and Geoelectricity,1993,45(9):841.
[9] 吴小平,徐果明.大地电磁数据的Occam反演改进[J].地球物理学报,1998,41(4):547.
[10]徐世浙,刘斌.大地电磁一维连续介质反演的曲线对比法[J].地球物理学报,1995,38(5):676.
[11]苏朱刘,罗延钟,胡文宝.大地电磁测深“正演修正法”一维反演[J].石油地球物理勘探,2002,37(2):138.
[12]严良俊,胡文宝.大地电磁测深资料的二次函数逼近非线性反演[J].地球物理学报,2004,47(5):935.
[13]陈小斌,赵国泽,汤吉,等.大地电磁自适应正则化反演算法[J].地球物理学报,2005,48(4):937.
[14]TONG X Z,LIU J X,XU L H.Damped Gauss-Newton optimization algorithm for two-dimensional magnetotelluric regularization inversion[A].International Conference on Information Engineering and Computer Science,2009.
[15]TIKHONOV A N,ARSENIN V Y.Solution of illposed problems[M].New York:Wiley,1977.
[16]FARQUHARSON C G,OLDENBURG D W.A comparison of automatic technique for estimating the regularization parameter in non-linear inverse problems[J].Geophysical Journal International,2004,156(3):411.
[17]FARQUHARSON,C G.Approximate sensitivities for the multi-dimensional electromagnetic inverse problem[D].University of Edinburgh,1990.
[18]HABER E,OLDENBURG D.A GCV based method for nonlinear ill-posed problems[J].Computational Geosciences,2000,4(1):41.
[19]柳建新,蒋鹏飞,童孝忠,等.不完全LU分解预处理的BICGSTAB算法在大地电磁二维正演模拟中的应用[J].中南大学学报:自然科学版,2009,40(2):484.
P 631.3+25
A
1001—1749(2012)01—0033—06
湖南省自然科学基金项目(10JJ6059);湖南省科研条件创新专项基金项目(2010TT2056)
2011-08-31
戴亦军(1975-),男,博士,主要从事电磁法正演模拟与反演成像。
