广义分数阶线性定常系统的状态响应
2012-01-11徐天博
徐天博
(大连交通大学 理学院,辽宁 大连 116028)
目前,几乎所有的以微分方程描述的控制系统,其微分均考虑为整数阶.实际上, 许多物理系统因其特殊的材料和化学特性而展现出分数阶动力学行为.实际系统通常大都是分数阶的,采用分数阶描述那些本身带有分数阶特性的对象时,能更好地揭示对象的本质特性及其行为.之所以忽略系统的实际阶次(分数阶),主要是因其复杂性和缺乏相应的数学工具.近年来分数阶相关成果不断涌现[1,2,3].当然,目前对分数阶系统的研究还不深入,尤其是广义分数阶系统的研究刚刚展开.本文定义了广义分数阶线性定常系统正则和p-δ函数,给出了状态方程解的一般表达式.
1 预备知识
1.1 分数阶微积分
分数阶微积分理论是研究任意阶微分和积分的,有关分数阶积分和微分的定义可见文献[1].
(1)Riemann-Liouville 定义

(2)Caputo定义
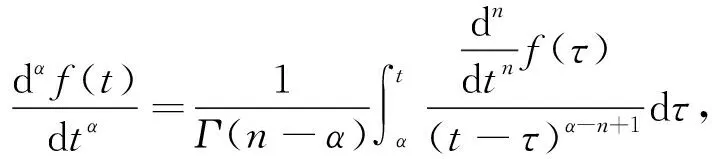
对Caputo分数阶微分取Laplace变换有
1.2 广义分数阶线性定常系统的状态方程可以描述为

2 广义分数阶线性定常系统及其解
广义分数阶线性定常系统的状态方程可以描述为
对广义分数阶系统进行受限等价变换:
当矩阵对(E,A)正则时,总存在可逆矩阵P,Q,使得

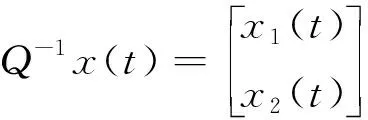
x1(t)∈Rr,x2(t)∈Rn-r,有
Dqx1(t)=A1x1(t)+B1u(t),y1(t)=C1x1(t)
(1)
NDαx2(t)=x2(t)+B2u(t),y2(t)=C2x2(t)
(2)
和整数阶广义系统中相类似,(1)、(2)式所作分解也称为快慢子系统分解,并称(1)式为慢子系统,(2)式为快子系统.
本文考虑如下正则的广义分数阶系统
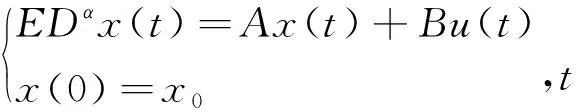
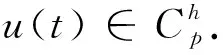
引理1[2,3]分数阶定常系统

引理2 定义P-δ函数

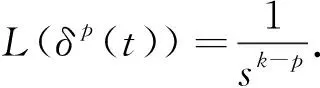
证明

令
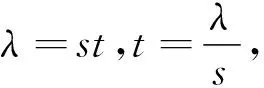
定理1 当t≥0时,广义分数阶定常系统
的状态响应为

(3)
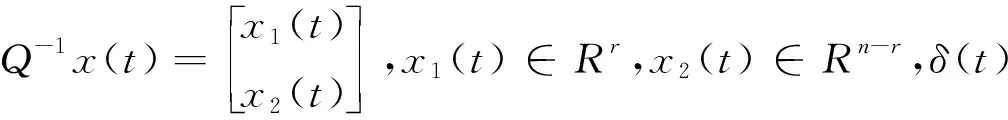

.
证明Dαx1(t)=A1x1(t)+B1u(t),y1(t)=C1x1(t)对慢子系统,对任意的初始状态,广义系统的解唯一,由引理1慢子系统的解为
(4)
另一方面,对快子系统NDαx2(t)=x2(t)+B2u(t),n-1<α 当矩阵对(E,A)正则时,有 . 所以 两边同时取Lapalace逆变换,有 (5) 其中 m=[αl+α-k-1]+1-(αl+α-k-1) 证毕. 可以看出,分数阶广义系统的解中含有类似于整数阶广义系统的脉冲项和输入的导数项. 参考文献: [1]Podlubny I.Fractional differential equations[M].San Diego:Academic Press,1999. [2]曾庆山,曹广益.分数阶线性系统的能观性研究[J].系统工程与电子技术,2004(11). [3]曾庆山,冯冬青,曹广益.基于分数阶微分方程描述的系统的能控性和能观性判据[J].郑州大学学报:工学版,2004(1). [4]杨冬梅,张庆灵,姚波.广义系统[M].北京:科学出版社,2004.



