非饱和土应力变量选取原则刍议

谢新宇 ，刘 斌 ，周 建

（1. 浙江大学 岩土工程研究所，杭州 310058；2. 浙江大学 软弱土与环境土工教育部重点实验室，杭州 310058）

1 引 言

在连续介质力学[1]中，本构方程或本构关系，是反映介质宏观性质的数学模型，包括反映纯力学行为的本构关系的Hooke 定律、Newton 黏性定律、Saint-Venant 理想塑性定律等和反映热力学性质的Clapeyron 理想气体状态方程、Fourier 热传导方程等。本构方程是理性力学研究的重要内容之一，是物体受外部作用发生响应时建立闭合可解方程的必要条件，也是在一定初始条件和边界条件下解决问题的基础。狭义的本构方程是指应力-应变的关系式，在非饱和土的研究中也大都是指描述应力-应变关系的方程。由此可见，应力是非饱和土本构模型的重要组成部分，也是研究本构关系的基础，正确选取非饱和土介质上的应力变量是建立本构方程的前提条件。随着越来越多的学者加入到非饱和土的研究领域，非饱和土本构模型得到不断发展，但一些学者在不断地追求更精确、更全面的非饱和土本构模型同时，却忽略了对非饱和土一些基本问题的斟酌，比如本构模型中应力变量选取问题，因为有的变量是不能直接应用于本构关系中的。这对后续学者的研究带来了不利影响，也阻碍了非饱和土本构模型的进一步发展。

自1959 年Bishop[2]在挪威奥斯陆市第1 次提出非饱和土的有效应力开始，Bishop 等[3]、Bolzon 等[4]又对Bishop 有效应力进行改进，后来发展到以Fredlund 等[5]提出的净法向应力（σ -ua，σ 为总应力，ua为土中的孔隙气压）和基质吸力（s= ua-uw，uw为土中的孔隙水压）为代表的双应力变量，再到现在Lu 等[6]提出的吸应力概念，非饱和土应力变量的选取一直是人们研究的热点问题，遗憾的是目前还没有一个统一的选取原则[7]，已有本构模型中应力变量选取的合理性也值得商榷。应力变量是建立正确本构模型的重要基础，鉴于此，本文从土体微观结构、能量守恒及力学平衡这3 个方面对非饱和土应力变量选取进行研究，提出非饱和土应力变量选取原则，在此基础上对现有广泛应用的应力变量进行分析，旨在为非饱和土本构理论研究提供合理的指导和依据。

2 应力变量选取原则

连续介质力学中应力变量指的是作用在物质内部单位面积上的力，它应与材料的性质无关，但对于土这种多孔、多相松散介质，由于孔隙压力是一种特殊应力，它与土体性质有关，故土中的应力变量有别于一般固体力学，可能含有材料参数[8]。与饱和土一样，本文用多孔介质力学中表征单元体积（REV，即Representative Elementary Volume）[9]的概念对应力变量进行阐述。REV 是可以代表材料力学、变形、渗透特性的最小单元，因此，应力变量也可定义为周边环境对介质REV 单位表面积上的作用力。由于非饱和土是固-液-气三相体，表征单元体积REV 也应由这3 相组成，故非饱和土的应力变量应是作用在三相体REV 单位表面积上的力。

本文根据应力变量的特性，提出了以下3 个原则判断一个应力变量是否作用在非饱和土上。

2.1 从微观结构角度分析

非饱和土中的应力变量是能够反映非饱和土特性的变量，它们应该是作用在非饱和土REV 上的各种应力。在非饱和土中，存在着各种应力，如孔隙压力、基质吸力、收缩膜张力、物理化学力等，它们作用的载体都不尽相同。比如传统的非饱和土力学中常用到ua与uw，从连续介质力学的角度上看，这些变量都是定义在单相体上的，即是分别定义在土中气和土中水单相体REV 上，如图1 所示[10]。

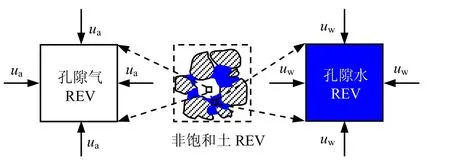
图1 非饱和土及单相体REV Fig.1 REV of unsaturated soil and single phase

而且传统定义的孔隙压力是一种非偏性力，即是各向同性的，如饱和土中的孔隙水压力，但在非饱和土中，无论是孔隙气压或是孔隙液压都可能作用在土颗粒局部区域上，从而形成偏性应力。因此，如果将这些变量视为是非饱和土的应力变量，则与前述的应力变量定义不符，即它们不是作用在非饱和土REV 上的应力。

图2 是饱和土和非饱和土中应力变量的对比图（为简化起见，图中未标出剪应力，且只考虑孔隙压力和骨架作用力）。

图2 非饱和土及饱和土应力变量 Fig.2 Stress variables of unsaturated soil and saturated soil

由图2(b)可见，饱和土中作用在REV 表面的应力变量有孔隙水压力uw、外力p 以及由控制土体强度和变形的粒间作用力fi经过面积归一化而得到的有效应力σ′，即σ′=∑ fi/A；在图2(a)所示的非饱和土受力简图中，由于气相的存在，在REV 表面分布有大小为uai、uwi的孔隙气压和孔隙水压，其对应的作用面积分别为Aai、Awi。若要将孔隙水压力和孔隙气压力视为应力变量，则需将其进行转换，即将这些在作用在相对小尺度单相体REV 上的应力变量转化到非饱和土REV 上，于是得到孔隙气应力aσ =∑uaiAai/A、孔隙水应力wσ =∑uwiAwi/A、有效应力σ′、外力p 等应力变量。

因此，在判断非饱和土应力变量时，必须考虑该应力变量所作用的介质，要将非饱和土中存在的各种作用力经过一定的转换作用到非饱和土REV上来。

2.2 从能量守恒角度分析

应力变量是1 个应力，连续介质力学中应力也等于物体产生单位体积或面积变化而消耗的能量。因此，应力的变化伴随能量的变化。自然界中，能量不会凭空产生，也无法凭空消失。所以，所选取的应力变量必须符合能量守恒定律。如果只考虑物体的“纯力学”行为，不包含热能、化学能、电磁能等其他形式的非机械能，则能量守恒规律表述为：介质动能加内能随时间的变化率等于外力的功率，这可从介质运动方程直接推出[1]：

式中：d/dt 为物质导数；ρ 为介质的质量密度；v为介质所占区域存在的速度场；∑为应力张量；b为单位质量的体积力。

Houlsby[11]将外力输入功率引起的土体变形和孔隙流体运动表示为

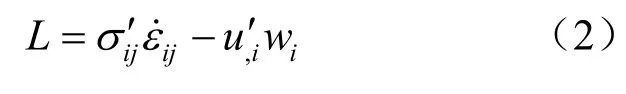
式中：ijσ′为非饱和土有效应力；ijε˙为应变率；，iu′ 为孔隙压力梯度；iw 为渗流场速度。

Houlsby 假设土颗粒和孔隙流体均为不可压缩，认为非饱和土在饱和度很高或是很低时孔隙中的流体相对于土颗粒是静止的，由此化简得到了非饱和土的功率平衡方程：

可见通过能量守恒原理而确定的应力变量才能反映非饱和土的力学特性。这里需要特别注意的是，非饱和土的应力变量反映的必须是非饱和土单位体积或面积变化而产生的能量，而不能是其他介质的能量，如ua、uw等，这些变量只是反映单相体单位体积或面积变化而产生的能量，因此，不能视为非饱和土的应力变量。

2.3 从力学平衡角度分析

连续介质力学中，单相体上的受力情况如图3所示[1]。作用在单相体表面的应力就为应力变量，包括法向应力和剪应力，共有6 个不同的应力变量。

图3 单相体REV 应力变量 Fig.3 Stress variables of single phase REV

传统的非饱和土力学模型中[12]，共有包括净法向应力（σ -ua）、基质吸力s 和剪应力τ 在内的7个应力变量。与饱和土相比，增加了基质吸力和净法向应力这2 个变量，这些应力变量共同作用在非饱和土REV 表面，且满足力学平衡，如图4 所示。

图4 传统的非饱和土REV 应力变量 Fig.4 Traditional stress variables of unsaturated soil REV

但在非饱和土多相体中，并不仅仅只有基质吸力和净法向应力对非饱和土的力学特性有影响，表面张力及其他物理化学应力等对其也有较大影响。为集中、全面地分析非饱和土的应力变量，必须在一个统一的参照物上进行分析，换句话说，应该把所有的应力转换到非饱和土REV 表面上，这可以通过转换参数X 把非饱和土中存在的各种应力转换到其REV 的尺度上。

这些作用在非饱和土REV 上的应力变量必须满足力学平衡，平衡方程如下：

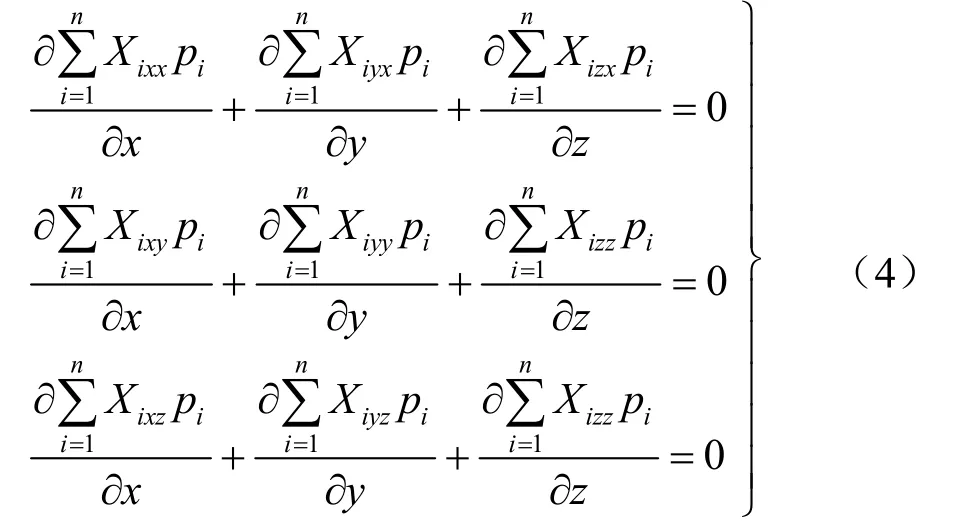
式中：pi为包括体积力、孔隙压力、界面张力、外力、物理化学力（如范德华力、电层力等）等在内的非饱和土中各种应力；Χikl为pi对应的转换参数，其将作用在微观介质上的非饱和土内部应力转换为非饱和土REV 表面上的各种应力变量。

2.4 讨论

从上述分析可以看到，较为合理地判断某变量是否是非饱和土中的应力变量应该从微观结构、能量守恒、力学平衡3 方面进行分析，三者缺一不可，只有同时满足3 方面的变量才能视为是非饱和土的应力变量。

应力变量作为非饱和土本构关系中的重要组成部分，不但对非饱和土的力学特性影响很大，对描述非饱和土的状态也有着重要意义，由于非饱和土的应力变量一般可以视为应力状态变量，如有效应力等，现有研究中就常将非饱和土应力变量与应力状态变量相混淆，这在很大程度上导致了本构模型中应力变量选择极为混乱的现状。

Fung[13]对状态变量做了如下定义：当已知某个系统、某一研究目标下的所有特性信息时，就可以确定该系统所处的状态，比如对于某一静止状态下的均质弹性体，要对其热力学状态进行完整的描述，这就需要知道其化学成分的含量、天然状态下的几何特征、应力场、应变场、表示物质冷热程度的物理量。这些物理量就是物质的状态变量。

若用上述的应力变量选取原则进行判别可发现，传统的非饱和土理论研究中，一些变量虽然不是作用在非饱和土上的应力变量，但对非饱和土变形、强度及流动特性等状态的描述具有重要作用，如孔隙压力等，这些变量便是应力状态变量，研究中不能忽视对它的判别，不能将其与应力变量混为一谈。

下面结合本文研究成果对近些年来非饱和土本构模型中选取的一些应力变量进行分析。

3 现有非饱和土应力变量分析

对于非饱和土本构模型中变量的选取，不同的学者有着不同的选择，大体上主要有净法向应力（σ -ua）、s、有效应力σ′等。有的学者定义了非饱和土有效应力，并作为唯一的应力变量描述非饱和土的特性，其目的是与传统的饱和土有效应力原理相结合，使非饱和土与饱和土之间能很好地衔接，便于工程设计及应用；但也有的学者认为，单应力变量不能很好地反映非饱和土的真实性状，尤其是变形特性，因此，建议采用多应力变量对非饱和土特性进行研究，这样描述的非饱和土特性与实际较吻合，由此引出的问题是本构关系中需要增加许多新的破坏准则、状态方程等，应用起来较为繁琐。

3.1 基质吸力

非饱和土总吸力包括基质吸力和渗透吸力两部分，实际工程中总吸力处于较低的水平，当总吸力较低时，基质吸力起控制作用，因此，长期以来对非饱和土吸力的研究主要侧重于基质吸力的研究。

（1）s 是非饱和土内部毛细管弯液面处空气压力与水压力的差值（ua-uw），单位与应力单位（kPa）相同，因此，许多学者将其定义为作用在非饱和土上的应力变量。s 由非饱和土中存在的气-液收缩膜引起，而不是非饱和土REV，此外组成s 的孔隙压力也都是定义在单相体上的应力。因此，从微观结构角度看，s 没有作用在非饱和土REV 上，不能视为是非饱和土的应力变量。

（2）从能量角度上来看，由前面Houlsby[11]提出的功率守恒方程发现，若s 是应力变量，则其对应的应变一定要是（+），这样才能满足功率守恒方程，而现有研究中，只有少数学者将s与其共轭应变对应起来（如Wheeler 等[14]）。另外还应特别注意，功率守恒建立的是非饱和土的能量平衡，而s 只是反映孔隙流体单位体积变化而产生的能量差或收缩膜单位体积变化的能量变化，因此，从能量的角度来看，s 未能反映非饱和土的能量变化，不满足应力变量的选取原则。

（3）从力学平衡上看，传统的非饱和土力学将

s 和净法向应力视为应力变量作用在非饱和土上，从而建立7 个变量间的力学平衡，该平衡是将基质吸力视为非偏性应力作用在非饱和土REV 上，然而组成s 的孔隙压力虽是非偏性应力，但孔压作用在骨架部分、非对称的接触面上，它对土体变形、强度的影响并不能体现出非偏性应力的特性，因此，将s 直接作用于非饱和土REV 上建立力学平衡是不合理的，需要经过一定的转换才能参与建立非饱和土力学平衡。Lu[10]也同样认为，s 不是应力变量，必须引入一个尺度转换函数Χ，将s 转换为作用在非饱和土REV 上的吸应力sσ ，才能参与建立力学平衡，如图5 所示。

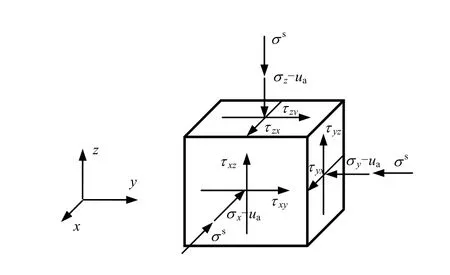
图5 考虑吸应力的非饱和土REV 应力变量 Fig.5 Stress variables of unsaturated soil REV that considering suction stress

综上所述，s 不能视为是非饱和土的应力变量，如果要在本构关系中使用，就要通过一定的转换，如Lu[10]提出的尺度转换，使其作用在非饱和土REV上。但试验研究结果表明，s 对土变形和强度等力学特性有着很大的影响，可见它是一个重要的应力状态变量。

3.2 净法向应力

净法向应力定义为总应力与孔隙气压的差值，即σ -ua，该应力变量广泛地应用于非饱和土的等吸力试验研究中。Fredlund[15]指出，土体饱和度为100%时，土中的孔隙气压等于孔隙水压，此时基质吸力为0，有效应力为σ -uw，故使用净法向应力能使饱和土与非饱和土间有很好的过渡，而且使用净法向应力可以使总应力的变化与孔隙水压力的变化区别开来，便于分析。大多数实际工程问题中，孔隙气压等于大气压力，气压力表量测的读数为0，即孔隙气压为0，净法向应力即为总应力，问题能得到简化。因此，净法向应力被大多数学者选用作为非饱和土的一个应力变量，现对其进行分析。

（1）从微观结构的角度来看，净法向应力中既有作用在单相气体上的孔隙气压，又有作用在非饱和土上的外部应力，仅用简单的数学关系将两者组合势必会引起应力作用尺度上的矛盾，因此，不能判断其作用在非饱和土REV 上，也不能视为是非饱和土的应力变量。

（2）从能量的角度上来看，由Houlsby 功率守恒方程得到，净法向应力与应变（ijε˙）共轭，可以满足功率守恒方程，但同样由于孔隙气体单位体积变化产生的能量不能与非饱和土单位体积变化产生的能量简单叠加，从而反映非饱和土的能量，因此，从能量的角度上看将净法向应力视为非饱和土的应力变量是不合理的。

（3）从力学平衡的角度上看，传统非饱和土力学简单地将总应力与孔隙气压力进行代数组合，将其视为非偏性应力作用在非饱和土上建立力学平衡。但实际上，净法向应力中的孔隙气压力并不是均匀作用于土颗粒周围的，孔隙气压的偏向性使其不能简单、均匀地作用于非饱和土REV 表面，故净法向应力和基质吸力一样，不能直接参与建立力学平衡。要使之成为非饱和土的应力变量，需要对其作一定的转换或与其他变量组合（如有效应力）。

由上述分析可以看出，常用的净法向应力也不是非饱和土的应力变量，不能直接用于本构方程中。各种试验结果表明，净法向应力实际上也是对非饱和土应力状态有重要影响的应力状态变量。

3.3 有效应力

自非饱和土概念提出以来，一直有许多学者致力于非饱和土有效应力的研究（Croney 等[16]，Bishop 等[3]，Aitchison[17]，谢定义等[18]，Lu 等[19]），他们希望将非饱和土中的有效应力与传统的Terzaghi 有效应力原理相结合起来，这样可以不用引入新的强度准则和状态方程，大大减小了设计和应用的难度。不过Jennings 等[20]及随后的许多学者也发现，单用非饱和土有效应力不能很好地反映非饱和土的强度特性和变形特性，尤其是部分非饱和土的湿陷性。下面对有效应力是否可以作为应力变量进行判别，以此分析用有效应力来研究非饱和土本构关系是否正确。

（1）从微观结构上分析，现有的非饱和土有效应力表达形式主要由2 项组成，一项是净法向应力；一项是关于基质吸力的函数，如Bishop 有效应力、谢定义提出的有效应力、Lu 有效应力等均如下表示：

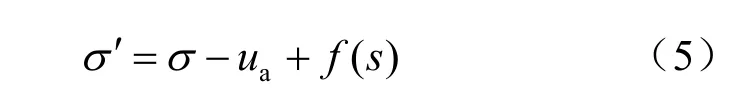
他们将作用在非饱和土表面及内部的各类应力（如孔隙压力、收缩膜张力、物理化学力、外力等）通过与相应参数（与饱和度Sr或体积含水量vθ 有关）耦合或是面积归一化后相加而得到有效应力，这类有效应力是以非饱和土为载体而进行研究的，因此，是作用在非饱和土REV 上，这是有效应力成为非饱和土应力变量的前提。

（2）从能量守恒上分析，利用Houlsby 功率守恒方程可以证明有效应力可以与应变（ijε˙）共轭，而且有效应力中虽然有反映单相体或者收缩膜等单位体积或面积变化而产生能量的孔隙压力和基质吸力等，但这些变量都经过一定的参数转化，使得它们的组合能用来表示非饱和土的能量，因此，满足能量守恒的原则。

（3）从力学平衡上分析，非饱和土有效应力如同饱和土中的有效应力，代表的是作用在非饱和土上能控制土体强度和变形特性的应力，是非偏性的，满足建立力学平衡的条件，因此，可以视为非饱和土的应力变量。

可见，有效应力可以作为非饱和土的应力变量并应用于本构方程中，而且有效应力影响着非饱和土的状态，同时也是一个应力状态变量。但现已确定的非饱和土有效应力还不足以全面反映非饱和土特性，因此，Kohgo 等[21]，Jommi 等[22]，Bolzon 等[4]，Gallipoli 等[23]，Wheeler 等[24]，Sun 等[25]，姚仰平等[26]将有效应力作为第1 应力变量，将与s 有关的函数作为第2 应力变量，利用双应力变量来描述非饱和土特性。

3.4 吸应力

Lu 等[6]将土体骨架中由于颗粒间的物理化学作用产生的力称为吸应力，包括黏结力、范德华力、毛管张力、负孔隙水压力等，从微观角度分析了非饱和土表征单元体积中存在的作用力，提出了一个尺度转换函数，将s 转换为作用在非饱和土上的应力变量——吸应力，具体表达式为[19]

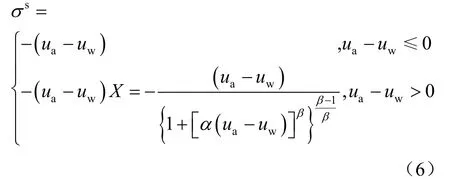
式中：sσ 可以通过Van Genuchten[27]提出的土-水特征曲线表达式求出；α 是孔隙的几何参数，数值上为进气压力值的倒数；β 为孔隙流体的参数，数值大小与孔隙分布有关。土颗粒越细，α 和β 的值越小。

由于sσ 是将非饱和土上存在的各种力通过尺度转换作用到非饱和土REV 上，故在微观上是合理的。将式（3）进行一定的变换可得：

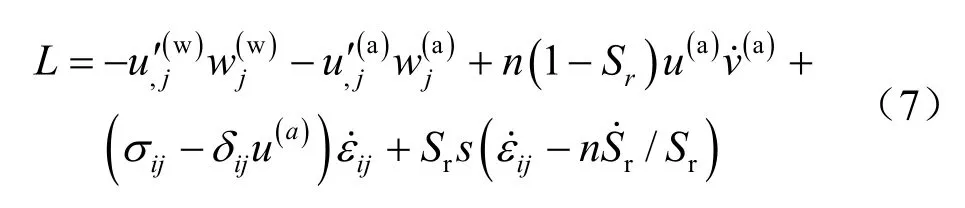
式中：第1、2 项是水、气在土中径流而耗散的能量；第3 项是气相压缩所需的能量；后2 项即是两对共轭的变量。

鉴于Lu 提出的 σs是关于饱和度的函数，由式（7）可知，（-/Sr）可视为吸应力的共轭应变，故满足Houlsby 功率守恒方程，且吸应力作用在非饱和土上，代表的是非饱和土单位体积变化产生的能量；最后，吸应力是s 经过尺度转换后形成的对非饱和土特性有重要影响的非偏性应力，可直接作用在非饱和土单元上，参与建立力学平衡方程。由此可以判断，吸应力可以作为非饱和土的一个应力变量。

3.5 讨论

通过对现有非饱和土模型所选取的应力变量分析发现，由于现有研究还没有明确提出应力变量的选取原则，致使一些应力变量的选取还不够准确。非饱和土应力变量必须作用在非饱和土表征单元体积REV 上且应满足力学平衡，而且反映的是单位非饱和土体积或面积变化的产生能量，一个变量只有完全符合这些选取原则时才能被定义为非饱和土的应力变量。一些变量（如净法向应力、基质吸力等）虽能满足功率平衡的要求，但没有作用在非饱和土REV 上，不能反映非饱和土的能量，这样的变量也不能作为应力变量。当然，这些变量虽然不能直接用于本构模型的建立，但在反映非饱和土状态时却有很大作用，因此，同样不能忽视对这些应力状态变量的研究。

总之研究非饱和土时，一定要注意选取变量的类型及选取的原则，分清应力变量与应力状态变量的关系，这样才不会错选应力变量。

4 结 论

（1）现有非饱和土本构模型中应力变量没有统一的选取标准。文中由微观结构、能量守衡及力学平衡3 方面确定了非饱和土应力变量的选取原则。经分析发现，净法向应力和基质吸力不是非饱和土的应力变量，而是应力状态变量。

（2）非饱和土有效应力（Bishop、谢定义、Lu等）和Lu 提出的吸应力将作用在非饱和土外部及内部的应力进行一定的变换从而作用于非饱和土REV 上，可以作为非饱和土的应力变量应用到本构模型中去；

（3）从现有的非饱和土本构模型来看，谢定义、Lu 等提出的非饱和土有效应力能很好地符合上述应力变量选取原则，且得出的非饱和土强度特性与实际情况较为吻合，但对变形问题还无法进行详细阐述，故一些学者建议选取多个应力变量，以更全面地反映非饱和土特性。但作者以为，不能因此认为有效应力在全面描述非饱和土特性时是无力的，反而应对现有有效应力的研究进行思考，就如谢定义在文献[8]中所提出的一些观点，总是存在有能反映非饱和土强度、变形特性的有效应力，就如同饱和土一样，可以发现一个简单应力变量来描述不同饱和度土体的特性。

（4）应力变量选取的正确与否决定着非饱和土本构关系研究是否合理，应该加以重视。本文提出的应力变量选取原则还不是十分严格，但通过这3个原则可以初步判断应力变量选取的合理性，可适当借鉴。本文旨在提出非饱和土本构研究中应力变量选取的问题并加以讨论，希望能引起研究者的注意，并通过不断研究，提出一个完善的非饱和土本构模型应力变量选取准则。

[1] 吕洪生， 曾新吾. 连续介质力学（上）-连续介质力学基础[M]. 长沙： 国防科技大学出版社， 1999.

[2] BISHOP A W. The principle of effective stress[J]. Tecknisk Ukeblad， 1959， 106 (39)： 859－863.

[3] BISHOP A W， BLIGHT G E. Some aspects of effective stress in saturated and unsaturated soils[J]. Géotechnique， 1963， 13(3)： 177－197.

[4] BOLZON G， SCHREFLER B A， ZIENKIWICZ O C. Elastoplastic soil constitutive laws generalized to partially saturated states[J]. Géotechnique， 1996， 46(2)： 279－289.

[5] FREDLUND D G， MORGENSTERN N R. Stress state variables for unsaturated soils[J]. Journal of Geotechnical Engineering Division, ASCE， 1977， 103(5)： 447－466.

[6] LU N， LIKOS W J. Suction stress characteristic curve for unsaturated soil[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE， 2006， 132(2)： 131－142.

[7] 周建. 非饱和土本构模型中应力变量选择研究[J]. 岩石力学与工程学报， 2009， 28(6)： 1200－1205. ZHOU Jian. Reseach on selection of stress variables of constitutive model for unsaturated soils[J]. Chinese Journal of Rock Mechanics and Engineering， 2009， 28(6)： 1200－1205.

[8] 谢定义. 对非饱和土有效应力研究中若干基本观点的思辨[J]. 岩土工程学报， 2006， 28(2)： 170－173. XIE Ding-yi. Consideration of some fundamental viewpoints in studying effective stress of unsaturated soils[J]. Chinese Journal of Geotechnical Engineering， 2006， 28(2)： 170－173.

[9] BEAR J. 多孔介质流体动力学[M]. 李竞生， 陈崇希译.北京： 中国建筑工业出版社， 1983.

[10] LU N. Is matric suction stress variable?[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE， 2008， 134(7)： 899－905.

[11] HOULSBY G T. The work input to an unsaturated granular material[J]. Géotechnique， 1997， 47(1)： 193－196.

[12] FREUND D G， RAHARDJO H. Soil mechanics for unsaturated soils[M]. New York： Wiley， 1993.

[13] FUNG Y C. Foundations of solid mechanics[M]. Englewood Cliffs： Prentice-Hall， 1965.

[14] WHEELER S J， SIVAKUMAR V. An elasto-plastic critical state framework for unsaturated soil[J]. Geotéchnique， 1995， 45(1)： 35－53.

[15] FREDLUND D G. Second canadian geotechnical colloquium： Appropriate concepts and technology for unsaturated soils[J]. Canadian Geotechnical Journal， 1979， 16(1)： 121－139.

[16] CRONEY D， COLEMAN J D， BLACK W P M. Movement and distribution of water in soil in relation to highway design and performance[J]. Highway Research Board Special Report， 1958， 40： 226－252.

[17] AITCHISON G D. Relationship of moisture and effective stress functions in unsaturated soils[C]//Golden Jubilee of the International Society of Soil Mechanics and Foundation Engineering at ICE. London： Butterworths， 1961： 47－52.

[18] 谢定义， 邢义川， 刘奉银. 非饱和土中力的传递机理及有效应力分析[J]. 西安理工大学学报， 2001， 17(1)： 1－5. XIE Ding-yi， XING Yi-chuan， LIU Feng-yin. Stress transmission mechanism and effective stress analysis of unsaturated soils[J]. Journal of Xi’an University of Technology， 2001， 17(1)： 1－5.

[19] LU N， GODT J， WU D. A closed form equation for effective stress in unsaturated soil[J]. Water Resources Research， 2010， 46： 1－29.

[20] JENNINGS J E B， BURLAND J B. Limitations to the use of effective stresses in partly saturated soil[J]. Géotechnique， 1962， 12(2)： 125－144.

[21] KOHGO Y， NAKANO M， MIYAZAKI T. Theoretical aspects of constitutive modeling for unsaturated soils[J]. Soils and Foundations， 1993， 33(4)： 49－63.

[22] JOMMI C， DI PRISCO C. Un semplice approcio teorico per la modellazione del comportamento meccanico di terreni granulari parcialmente saturi[C]//Conference Ilruolo dei Fluidi nei Problemi di Ingegneria Geotecnica. [S. l.]： Mondovi， 1994： 167－188.

[23] GALLIPOLI D， GENS A， SHARMA R， et al. An elastoplastic model for unsaturated soil incorporating the effects of suction and degree of saturation on mechanical behavior[J]. Géotechnique， 2003， 53(1)： 123－135.

[24] WHEELER S J， SHARAMA R J， BUISSON M S R. Coupling of hydraulic hysteresis and stress-strain behavior in unsaturated soils[J]. Géotechnique， 2003， 53(1)： 41－54.

[25] SUN D， SHENG D， SLOAN S W. Elastoplastic modeling of hydraulic and stress-strain behavior of unsaturated soils[J]. Mechanics of Materials， 2007， 39(3)： 212－221.

[26] 姚仰平， 牛雷， 杨一帆， 等. 考虑温度影响的非饱和土本构模型[J]. 岩土力学， 2011， 32(10)： 2881－2888. YAO Yang-ping， NIU Lei， YANG Yi-fan， et al. Constitutive model for unsaturated clays considering temperature effects[J]. Rock and Soil Mechanics， 2011， 32(10)： 2881－2888.

[27] VAN GENUCHTE M Th. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal， 1980， 44(5)： 892－898.