混合型缓冲回填材料非饱和水分扩散试验研究
2012-01-08张虎元贾灵艳
张 明,张虎元,贾灵艳
(兰州大学 西部灾害与环境力学教育部重点实验室,兰州 730000)
1 引 言
纯膨润土作为缓冲回填材料,虽然可以最大限度地发挥其防渗性能、膨胀自愈性能和吸附性能,但纯膨润土存在着可施工性差、材料强度低等弊端。向膨润土中添加石英砂,可显著提高其可施工性和力学强度[1-2]。另外,与其他添加剂相比,石英砂储量丰富且相对廉价,缓冲回填材料添加石英砂也不会明显增大工程成本。
处置库运行之后,缓冲回填材料要经历很长的时间才能达到饱和状态。处置库运行初期,靠近围岩一侧的缓冲回填材料受到地下水的浸润,逐渐吸水产生膨胀应力,缓冲材料的干密度也可能随之发生变化。在浸水过程中,缓冲材料的干密度也会发生变化。缓冲回填材料的非饱和导水率特别是液态形式水的非饱和导水率可间接反映溶质的迁移能力。因此,研究缓冲材料浸水过程有着很重要的理论及工程意义。
关于膨润土-砂混合物浸水规律的研究,国内外已取得了一定的研究成果。Mata 等[3]通过室内和现场浸水试验研究了不同离子及浓度对水分迁移的影响。Villar[4]发现,溶液离子会促进混合物吸收水分。在浸水试验结束后实测了离子含量与干密度在试样中的分布。Börgesson 等[5]研究了温度对膨润土的非饱和导水率的控制作用。Kanno 等[6]研究了干密度对膨润土-砂混合物非饱和导水率的影响,认为干密度越大,非饱和导水率越小。Cui 等[7]研究了不
同膨胀条件下膨润土-砂混合物非饱和导水率的差异。叶为民等[8]采用自制仪器测试了GMZ001 膨润土在非膨胀条件下的非饱和导水率。
本研究采用自制的浸水试验装置,实测掺砂率为30%的GMZ001 膨润土-砂混合物浸水后干密度和水分分布曲线,分析混合物的非饱和导水率,试图区分水分的汽/液迁移形式。同时,对浸水过程中混合物两端的应力进行监测,所测结果可为我国混合型缓冲回填材料优化配比提供依据。
2 材料与方法
2.1 试验材料
试验所用高庙子膨润土主料由核工业北京地质研究院提供,简称“GMZ001 膨润土”,产自内蒙古兴和县高庙子地区。石英砂骨料为人工加工的标准砂,产自我国石英砂岩六大储藏地之一的甘肃永登县奖俊埠,由富隆石英砂厂生产。试验材料基本性质见表1。

表1 试验材料基本性质[9-10] Table 1 Basic properties of test material
2.2 试验方法
定义石英砂与膨润土-石英砂混合物的干重之比为掺砂率(Rs)。将烘干的膨润土与石英砂按掺砂率为30%的比例混合后充分搅拌,根据设计的压制含水率计算所需水量,按喷雾法将蒸馏水喷入样品均匀湿化,将土样置于保湿器中密封润湿60 h。参考张虎元等[10]的方法,采用CSS-WAW300 型电液伺服万能材料试验机进行压实制样(浸水试验设计见表2)。

表2 浸水试验设计及试样参数 Table 2 Physical parameters of specimens for infiltration tests
图1 是设计加工的专用浸水试验装置。压实试样切入环刀(高为40 mm,直径为60 mm)内,环刀和刚性夹具共同限制试样的膨胀变形。夹具与试样之间安置透水石。试样两端放置一层滤纸。装入试样的装置浸入蒸馏水中,水面维持在样块中间,认为水头为0(见图1)。试样底端称为“渗入端”,顶端称为“渗出端”。每个浸水试验周期结束后将试样切成2 mm 厚薄片,用烘干法量测各薄片质量含水率,确定试样的水分分布曲线。试样的初始含水率0ω 相同,即12.3%(最优含水率),初始干密度基本相同,可视为平行试样,试验水温为20 ℃。试验目的见表2。

图1 浸水试验装置简图 Fig.1 Schematic of water infilitration test apparatus
3 试验结果
3.1 水分分布
试样S1、S2、S3、S4 分别经历8、24、48、 96 h 浸水试验后,实测的水分分布曲线如图2 所示。由于4 个试样的初始干密度基本相同,图中不同时间的水分分布曲线,可以看成同一个试样经历不同浸水时间后水分分布曲线的依次演变过程。由图可知,渗入端一侧的含水率迅速升至25.4%,并在随后的8~96 h 浸水过程中,含水率仅升高了1.67%。与此相对应,试样内部的浸润锋面在浸水8 h 后推移至15 mm 深,浸水24 h 后推移至约30 mm 深,浸水96 h 后推移并超出渗出端。不同浸水时间在深度zi处的含水率ω(%),即水分分布曲线,可用表3 的拟合方程进行描述。

图2 不同浸水周期的水分分布曲线 Fig.2 Water content distributions at different infiltration periods

表3 试样水分分布曲线拟合方程 Table 3 Fitted equations for distributions of water contents
3.2 干密度分布
试样S5 安装于浸水试验装置后移入保湿器中静置96 h 作为参比;试样S6 安装于浸湿试验装置中按图1 所示的方式浸水96 h。试验结束后,将试样切成厚度均为8 mm 的薄片,采用烘干法分别量测其干质量并计算干密度。图3 是试样S5、S6 的干密度分布曲线。由图可以看出,未经浸水的试样S5,干密度峰值出现在试样中部。这说明采用张虎元等[10]的双压头单轴静力压实法获得的试样,中部密度偏高,两端密度偏低。与此相比,采用相同方法制备但经过浸水之后的试样S6,干密度峰值比S5有所降低,峰值位置由原来的试样中部(即20 mm处)偏移到距渗入端约30 mm 处;试样S6 两端部的干密度比S5 有所提高。换言之,浸水之后,试样中部的干密度有所下降,两端的干密度有所提高,即试样干密度原有的不均匀分布有所缓和。这说明,在围限条件下,混合物吸水膨胀变形有使内部密度向均一化调整的趋势。
撤除刚性限制之后,试样材料会发生一定程度的膨胀,采用切片烘干法测定干密度也会对试样原有状态产生一定程度的扰动,因此,与理想真值相比,实测干密度会包含一定的误差。但对揭示不同位置的干密度分布还是很有价值的。

图3 浸水前后干密度分布变化 Fig.3 Distributions of dry density before and after water infiltration
3.3 应力发展
在试样S7 的渗入端及渗出端分别安置BX-1 型土压力传感器,连接YJ-35 型静态电阻应变仪,通过标定系数求出不同时刻试样受到刚性限制产生的应力。图4 为应力随时间的变化曲线。浸水96 h 后,渗入端的最大应力值为1.02 MPa;试样渗出端的最大应力值为1.00 MPa。由图可知,浸水初期,混合物渗入端应力增大很快,但24 h 后明显减慢。相反,渗出端的应力一直保持持续增长。图4 表明,浸水96 h 之后,渗入端与渗出端的应力值基本接近。
如图5 所示,试样浸水后会受到3 种力的作用:上、下刚性限制的约束力P1与P2、与环刀侧壁的摩擦力f 以及垂直于侧壁方向的约束力F。而仪器读数则为P1与P2的反作用力所对应的应力值,并不与试样的实际膨胀应力对等。
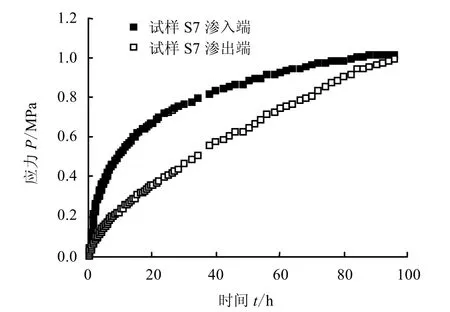
图4 应力-时间关系 Fig.4 Curves of stress-time
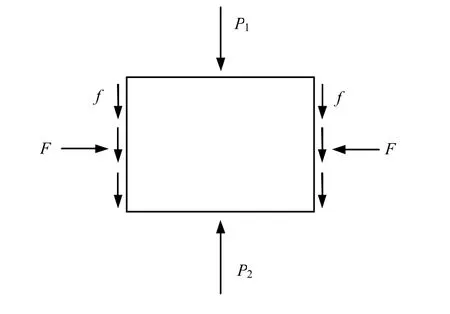
图5 试样受力分析 Fig.5 Sample stress analysis
试样压制进入环刀,材料与环刀侧壁紧密接触,两者之间存在很大的摩擦力。这一点,从试样从环刀里脱出可以验证。试样从环刀内脱出,环刀内侧可以明显看到材料表面上的擦痕。由于摩擦力的存在,试样顶部及底部的约束力会有差异。
4 讨 论
4.1 水分扩散系数与非饱和导水率的关系
非膨胀条件下膨润土-砂混合物试样一维水分迁移可用下式表达[11]:

式中:Q 为迁移水量;k 为非饱和导水率;z 为标高;ψ 为孔隙水势,包括基质势、重力势和渗透势。
孔隙水势有多种表达方式,如单位质量含有的能量、单位体积含有的能量和单位重量含有的能 量[12]。本研究中,孔隙水势定义为单位重量所含能量,意义等价于水头。混合物中水分重力势的影响可以忽略,因此,非饱和水流可用下式表达[11]:
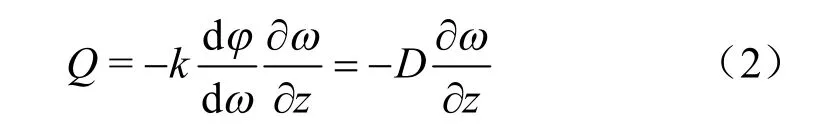
其中

式中:D 为水分扩散系数;ω 为质量含水率;φ 为基质势与渗透势之和;d dω φ 为比水重度。
4.2 水分扩散系数
对试样长度l 中的某一位置zi而言,从时间t1到t2的水分扩散系数,可在浸水试验得到的水分分布曲线的基础上按照下式计算:
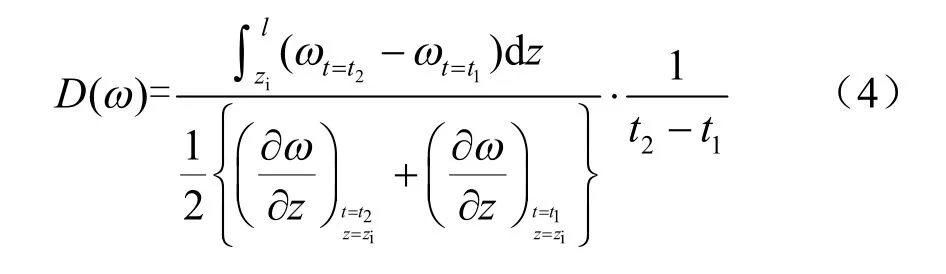
式中:t 为浸水时间;l 为试样长度;zi(0≤zi≤l)为测试点到渗入端的距离。
利用式(4)及图2 的水分分布曲线,可以求出混合物不同含水率时的水分扩散系数。图6 中的黑点是基于式(4)对实测数据进行准确计算的数值,图中的曲线是采用式(10)对实测数值进行拟合后的结果。水分扩散系数取决于水分分布曲线,形如U 型。最小值出现在含水率为23.5%附近。

图6 混合物水分扩散系数与含水率关系 Fig.6 Relationship between water diffusivity of bentonite-sand mixtures and water content
水分扩散包括汽态水和液态水2 种形式的扩散。随着含水率增大,水分迁移形式从汽态占主导逐渐过渡为液态占主导。汽态水扩散系数Dv可用Philip 等[13]提出的等式表达;液态水扩散系数Dl可用Darcy 公式表达。有研究表明,汽态水和液态水扩散系数都受 φ ω∂ ∂ 控制,即水分扩散系数可以表达成含水率的函数[14],见下式。

且存在式(6)、(7)2 个边界条件:

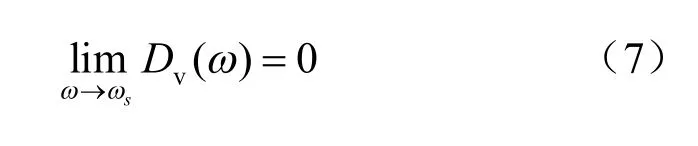
随着含水率增大,试样中液态水迁移量增多,汽态水迁移量逐渐减少。由不等式理论可知,当汽态水分扩散系数Dv与液态水分扩散系数Dl相等时,两者之和最小。如图7 所示,首先假设水分扩散系数U 型曲线最低点,Dv=Dl=1/2Dmin,即水分扩散系数最小值的1/2 为汽态水分扩散系数,另一半为液态水分扩散系数。用光滑曲线连接1/2Dmin与饱和时扩散系数,即得到右侧液态水分扩散系数。汽态水分扩散系数可由水分扩散系数减去液态水分扩散系数得到。同理,可估算出水分扩散系数最小值左侧的汽态水分扩散系数和液态水分扩散系数。由曲线形式可知,汽态水分扩散系数符合下式:

液态水分扩散系数符合下式
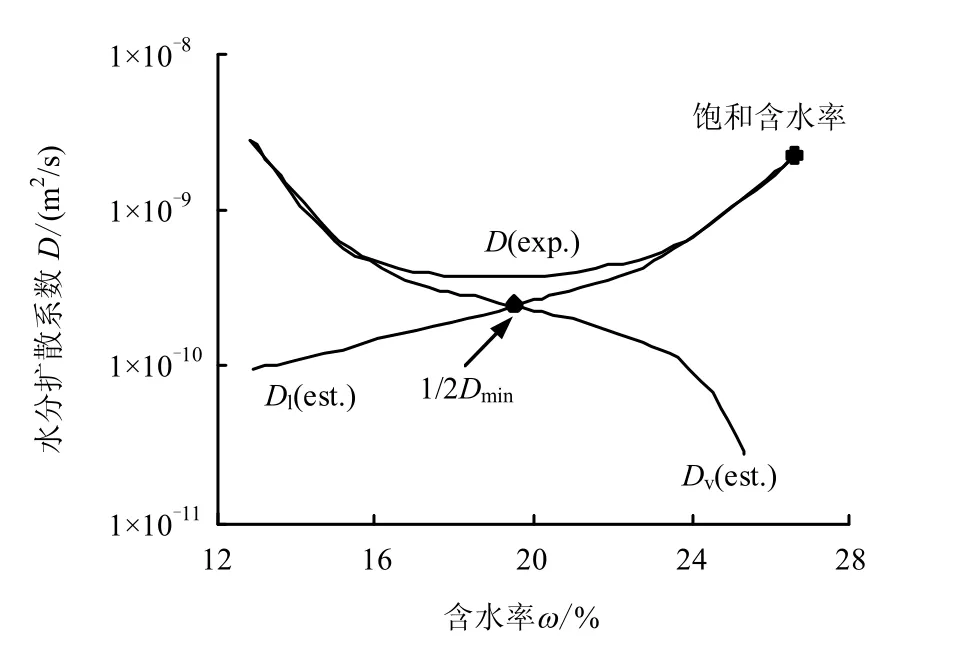
图7 汽态及液态水分扩散系数估算方法 Fig 7 Method for estimating water vapor and liquid water diffusivity
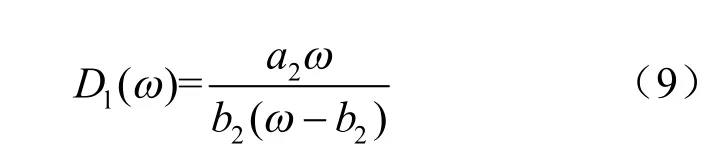
所以,水分扩散系数应满足
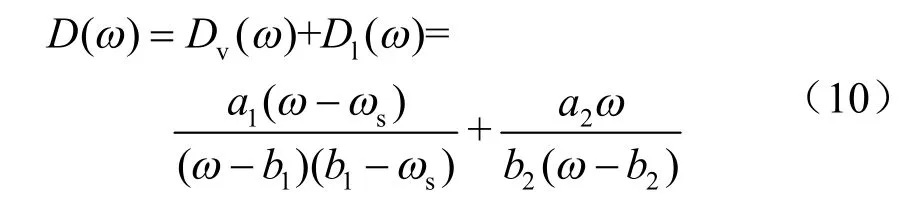
式中:v( )D ω 为汽态水分扩散系数;l( )D ω 为液态水分扩散系数;sω 为试样饱和含水率;a1、a2、b1和b2为拟合系数。由试验结果得到:a1=28.26,a2= -1.42×10-7,b1=-651,b2=0.276,sω =0.279。图8是将水分扩散系数分解为汽态水分扩散系数和液态水分扩散系数之后的结果。由图可知,随着含水率增加,汽态水分扩散系数单调递减,而液态水分扩散系数单调递增。理论上讲,含水率达到最大值时,汽态水分扩散系数趋近于0,液态水分扩散系数达到最大,即等于饱和时混合物的水分扩散系数。
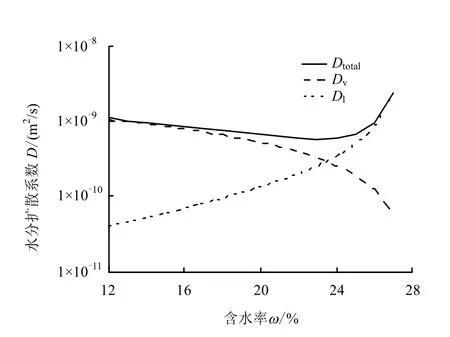
图8 利用式(10)估计汽态及液态水分扩散系数 Fig 8 Estimated water vapor and liquid water diffusivity according to Eq. 10
4.3 非饱和导水率
前期试验[15]获得的膨润土-砂混合物修正土-水特征曲线方程为

由式(3)、(10)和(11)可知,水分非饱和导水率(ktotal)为汽态水非饱和导水率(kv)与液态水非饱和导水率(kl)之和,即:
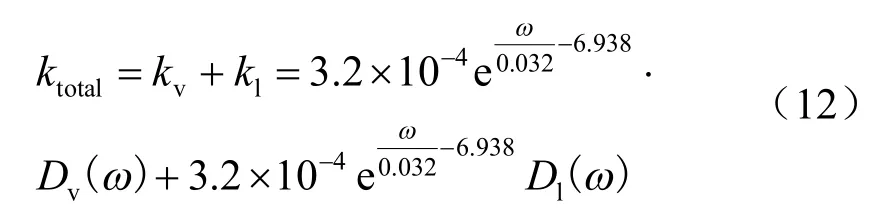
两者共同描述的混合物非饱和导水率绘于图9。由图可知,随着含水率的增加,混合物汽态水分非饱和导水率先增大后略有减小;液态水非饱和导水率始终增大。随着含水率的增加,膨润土-砂混合物非饱和导水率增大。含水率约为12.0%时,非饱和导水率最小,约为1.45×10-14m/s。含水率约为27.0%(试样接近饱和)时,非饱和导水率最大,约为3.40×10-12m/s。由此可见,混合物非饱和导水率的最大值与最小值之间相差2 个数量级。
核废料处置工程屏障中,溶质的迁移形式主要是以液态水为载体而进行的。而膨润土缓冲回填材料几乎不可能达到饱和状态。因此,液态水非饱和导水率可作为评价缓冲材料性质优劣的重要指标。液态水分非饱和导水率越低,缓冲材料的溶质迁移能力越弱。
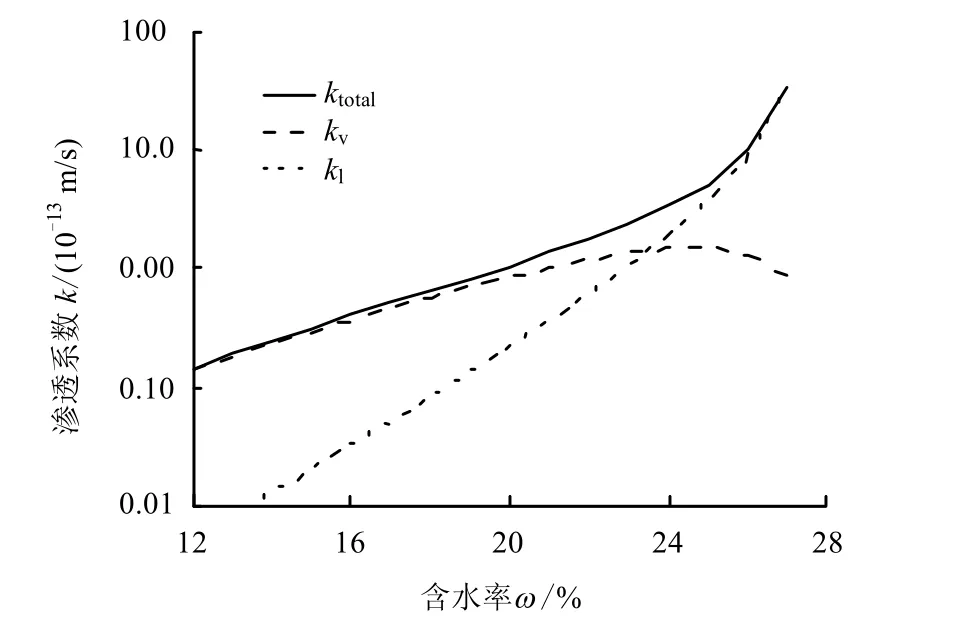
图9 混合物非饱和导水率 Fig 9 Estimated unsaturated hydraulic conductivity of bentonite-sand mixtures
5 结 论
(1)膨润土-砂混合物浸水后干密度会发生变化。混合物初始压制完成后,干密度最大值维持在试样中间位置,两端部偏小。浸水96 h 的试样干密度最大值位置向渗出端偏移,干密度分布趋于均一。
(2)随着浸水时间的增加,膨润土-砂混合物渗入端应力快速增长,随后减缓;渗出端应力持续缓慢增长。浸水96 h 后,两端应力趋于一致。
(3)混合物的水分扩散系数可分解成汽态水分扩散系数和液态水分扩散系数。随着含水率的增加,前者单调减小,后者单调增大。整体上,混合物的水分扩散系数随含水率变化呈U 型特征。
(4)混合物的非饱和导水率可分解为汽态水分非饱和导水率和液态水分非饱和导水率。随着含水率增加,前者缓慢增大,随后略有减小;后者单调增大。混合物的非饱和导水率随含水率增加单调增大,数值变化在1.45×10-14~3.40×10-12m/s 之间。
[1] GRAY M N, CHEUNG S C H, DIXON D A. The influence of sand content on swelling pressures and structure developed in statically compacted Na-bentonite[R]. Canada: AECL, 1984.
[2] DIXON D A, GRAY M N, THOMAS A W. A study of the compaction properties of potential clay-sand buffer mixtures for use in nuclear fuel waste disposal[J]. Engineering Geology, 1985, 21(3-4): 247-255.
[3] MATA C, GUIMARÃES L DO N, LEDESMA C A, et al. A hydro-geochemical analysis of the saturation process with salt water of a bentonite crushed granite rock mixture in an engineered nuclear barrier[J]. Engineering Geology, 2005, 81(3): 227-245.
[4] VILLAR M V. Infiltration tests on a granite/bentonite mixture: Influence of water salinity[J]. Applied Clay Science, 2006, 31: 96-109.
[5] BÖRGESSON L, CHIJIMATSU M, FUJITA T, et al. Thermo-hydro-mechanical characterisation of a bentonite-based buffer material by laboratory tests and numerical back analyses[J]. International Journal of Rock Mechanics & Mining Sciences, 2001, 38: 95-104.
[6] KANNO T, FUJITA1 T, TAKEUCHI1 S, et al. Coupled thermo-hydro-mechanical modelling of bentonite buffer material[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1999, 23: 1281-1307.
[7] CUI Y J, TANG A M, LOISEAU C, et al. Determining the unsaturated hydraulic conductivity of a compacted sand-bentonite mixture under constant-volume and free-swell conditions[J]. Physics and Chemistry of the Earth, 2008, 33: 462-471.
[8] 叶为民, 钱立鑫, 陈宝, 等. 侧限状态下高压实高庙子膨润土非饱和渗透性的试验研究测试[J]. 岩土工程学报, 2009, 31(1): 105-109. YE Wei-min, QIAN Li-xin, CHEN Bao, et al. Laboratory test on unsaturated hydraulic conductivity of densely compacted Gaomiaozi bentonite under confined conditions[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(1): 105-109.
[9] 刘月妙, 温志坚. 用于高放射性废物深地质处置的黏土材料研究[J]. 矿物岩石地球化学通报, 2003, 23(4): 42-45. LIU Yue-miao, WEN Zhi-jian. Study of clay-based materials for the repository of high level radioactive waste[J]. Bulletin of Mineralogy Petrology and Geochemistry, 2003, 23(4): 42-45.
[10] 张虎元, 梁建, 刘吉胜, 等. 高庙子膨润土与砂混合物的击实性能研究[J]. 岩石力学与工程学报, 2009, 28(12): 2585-2592. ZHANG Hu-yuan, LIANG Jian, LIU Ji-sheng, et al. Role of sand content on the shear strength of compacted bentonite-sand mixtures as buffer/backfill material for HLW disposal[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(12): 2585-2592.
[11] FREDLUND D G, RAHURDJO H. Soil mechanics for unsaturated soils[M]. New York: John Wiley & Sons, 1993: 125-135.
[12] SMITH K, MULLINS C. Soil analysis-physical methods[M]. New York: Marcel Dekker, 1991.
[13] PHILIP J R, DE VRIES D A. Moisture movement in porous materials under temperature gradients[J]. Am. Geophys.Union Trans., 1957, 38(2): 222-232.
[14] NASSER H. Hydromechanical and thermo-hydro- mechanical behaviour of deep argillaceous rock[M]. Netherland: Swets & Zeitlinger, 2002: 23-33.
[15] 张虎元, 张明, 崔素丽, 等. 混合型缓冲回填材料土水特征曲线测试与修正[J]. 岩石力学与工程学报, 2011, 30(2): 382-390. ZHANG Hu-yuan, ZHANG Ming, CUI Su-li, et al. Determination and modification of soil water characteristic curves of bentonite-sand mixtures as HLW backfill/buffer material[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(2): 382-390.
