地应力与岩石弹性模量关系试验研究

秦向辉 ，谭成轩 ，孙进忠，陈群策 ，安美建

（1. 国土资源部新构造运动与地质灾害重点实验室，北京 100081；2. 中国地质科学院地质力学研究所，北京 100081；

3. 中国地质大学 工程技术学院，北京 100083）

1 引 言

实践证明，地壳浅表层地应力状态研究对于深部矿产开采、地震监测预报、区域地壳稳定性评价、煤瓦斯突出等研究等具有十分重要的意义[1－4]。而地壳浅表层地应力状态受很多因素影响，诸如岩性、岩体结构、岩石力学性质、地质构造条件、地形地貌条件等[5－6]，具有一定的复杂性和未知性，前人在地应力与岩性、岩体结构等方面进行了一些有意义的探讨，但一些认识仍需要不断完善和发展，如地应力大小与弹性模量、岩体完整性等之间的定量关系，需要开展系统的试验研究，尤其是钻孔不同深度地应力测量、岩石力学试验及其对比分析系统研究，因为已有研究成果多为平面二维资料。

本文主要基于深孔地应力测量、岩石力学试验及岩体结构统计，对地应力与岩石弹性模量关系进行了研究。

2 已有研究成果和认识

2.1 岩性对地应力大小的影响

岩性是影响地应力大小的一个重要因素，其对地应力影响的主要原因是岩石材料的变形性质。岩石形成的地质环境、岩石成分以及后期改造作用都会影响岩石的变形性质，从而影响地应力的大小，相关研究者对实测地应力的分析成果以及相关的理论研究都证明了这一点[7－10]。

2.2 岩体结构对地应力状态的影响

结构面使岩体完整性受到了破坏，导致岩体物理力学性质发生变化，进一步影响地应力状态，也是实测地应力值具有分散性的一个重要原因。造成岩体物理力学性质变化的岩体结构主要有断层（裂）、节理等结构面。断裂直接影响地应力的分布特征，使断裂附近地应力大小和方向发生突变，也可以形成完全有别于区域应力场的局部应力场，国内外相关研究者对一些断裂附近的地应力测量已经证明了这一点[11－14]；节理使岩体的力学性质弱化，从而间接影响地应力的分布状态，已有研究者在地应力测量及结果分析、地应力与岩石力学性质关系研究中考虑了岩体结构的影响，并尝试了将岩体结构的影响引入到地应力与岩石弹性模量之间关系分析中[15－16]。

2.3 岩石力学性质对地应力状态的影响

在其他条件相同的情况下，岩石力学性质差异也会造成地应力状态的不同，影响地应力状态的主要岩石力学参数包括弹性模量、抗压强度等。相关研究者通过试验并结合理论分析，研究了不同岩石和地应力环境下地应力大小与岩石力学性质间的关系[16－18]。已有研究成果表明，地应力状态和围岩力学性质之间存在密切的相关性，岩性、岩体结构影响岩体强度（抗压、抗张、抗剪）、弹性模量、泊松比、内摩擦角、凝聚力等力学指标，进而影响地壳浅表层地应力大小，同时岩体结构构造对主应力方向有重要影响。但到目前为止，已有研究成果普遍认为，岩石力学性质与地应力之间有一定的关系，但缺乏定量化，并且多为区域平面二维数据的收集整理和统计分析，缺少典型钻孔随深度的系统研究。

基于前人的研究程度，尝试依托深孔不同深度系统地应力测量、详细的岩体结构统计，配合岩石力学试验，对地应力与岩性、岩体结构及岩石力学性质之间的关系进行分析探讨。

3 典型钻孔地应力与围岩力学性质关系试验分析

3.1 北京平谷深孔地应力测量结果分析

地应力测量钻孔位于北京市平谷区南独乐河镇南山村盘山花岗岩体（E117°16′15″，N40°08′05″，高程为155 m），构造上位于东西向纬向断裂构造带与北北东向新华夏系活动断裂构造带（夏垫活动断裂）交汇之北东象限，历史上1679 年9 月曾在马坊附近发生过Ms8 级地震，属于北京地区关键构造部位之一。钻探深度为600.47 m，全孔采取岩芯，并进行钻孔岩芯详细编录和岩体结构系统统计分析。钻孔岩芯详细编录揭示：0～413.13 m 为花岗岩；413.13～500.83 m 为矽化灰岩；500.83～508.14 m 为花岗岩；508.14～600.47 m 为灰岩（见图1）。

图1 北京平谷深孔钻孔柱状图 Fig.1 Deep borehole histogram in Pinggu, Beijing

依据岩芯的完整性，采用国际岩石力学学会推荐的水压致裂法进行了随深度的地应力测量，压裂曲线与国际岩石力学学会推荐的水压致裂法标准曲线形态相似（见图2），采用国际岩石力学学会推荐的5 种方法之一的dt/dp 法进行了数据处理[19]，获得了较准确的各深度段地应力值及主应力随深度的变化情况（见表1、图3）。通过对地应力测量结果分析认为：（1）该深孔地应力的分布规律同国内外已有认识基本一致；（2）在200～370 m 间出现应力集中，应力值明显高于正常变化趋势，这主要是受测点附近的地形地貌影响，导致应力集中；（3）在370 m 以下，地应力随深度正常增加，属于正常变化范围；（4）同国内已有的华北地区地应力资料对比表明，该构造部位近地表现今地应力大小是华北地区同等深度和同一岩性平均值的1.5～2.0 倍，属于现今构造应力场敏感构造部位[20]。

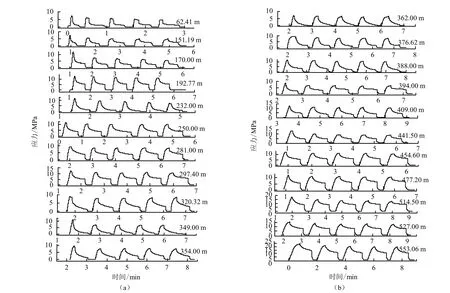
图2 水压致裂应力测量曲线 Fig.2 Curves of hydraulic fracturing in-situ stress measurement

表1 水压致裂应力测量结果 Table 1 Results of hydraulic fracturing in-situ stress measurement

图3 北京平谷深孔实测主应力大小随深度分布特征 Fig.3 Variations of in-situ stress vs. depths in Pinggu deep borehole, Beijing

3.2 室内岩石力学试验

该地应力测量钻孔有花岗岩、矽化灰岩和灰岩3 种岩性，同时，整个钻孔岩体结构变化较大，是进行地应力大小与岩性、岩体结构和岩石力学性质之间关系研究的理想钻孔。为此，在地应力测量同等深度进行岩芯取样，开展单轴压缩试验（UCT）和常规三轴岩石力学试验。试验采用TAW-2000 微机控制电液伺服岩石三轴试验机。试样按照ISRM的建议制成直径为50 mm、高为100 mm 的标准样，三轴试验的围压分别为5、10、15 MPa，表2 给出了岩石力学试验获得的岩石弹性模量。

在岩石力学试验中进行了单轴及5、10、15 MPa不同围压的三轴试验，而不同深度的岩石仅有一个与深度相关的围压能反映其所处的真实地质环境。本文首次尝试将岩石所在实际深度的平均水平主应力值作为岩石所处的围压，即(SH+Sh)/2，表3 给出了不同应力测量段的围压。由于岩石力学试验中设定的围压和应力测量段的围压并不相同，因此，需要将两者结合起来，本文参考岩石弹性模量与围压关系相关研究成果[21－22]，对岩石弹性模量和围压进行指数公式拟合，获得了不同测量段的岩石弹性模量（见表3）。

岩体是由岩块和切割岩块的各种结构面构成的，结构面的存在，使岩体的力学性质和岩石的力学性质存在着较大差别，岩块的力学性质可以通过室内的岩石力学试验获得，而岩体的力学性质，最准确和直接的手段是通过现场试验，但现场岩体力学试验不仅复杂而且成本相对较高，因而通过研究岩块的力学性质以及岩体结构对岩石物理力学性质的影响规律，进而评价岩体的性质已经成为许多研究者尝试的方式之一[23－24]。在岩石力学试验的基础上，综合已有研究成果，考虑岩体结构（岩体完整性指标－RQD）的影响，借鉴前人的Em=E·RQD式，对岩石弹性模量（E）进行了修正（见表3）[16]。

表2 岩石力学试验结果 Table 2 Results of rock mechanical test

表3 应力测量深度对应围压条件下岩石弹性模量 Table 3 Elastic modulus of rock in corresponding confining pressure in in-situ stress measuring depths

3.3 地应力大小与岩石弹性模量相关分析

在对上述原岩应力测量和岩石力学试验分析的基础上，对比研究了花岗岩和灰岩中主应力大小（水平最大主应力、水平最小主应力）与岩石弹性模量（修正前为E，修正后为Em）间的关系。

在进行花岗岩中主应力大小与岩石弹性模量关系分析时，滤掉了应力集中范围内的应力值明显偏离正常变化范围的4 个点（深度分别为192.77、250.00、281.00 和297.40 m），分析表明，4 个测点并不影响地应力与岩石弹性模量的相关性。图4、5和表4 给出了花岗岩中水平最大主应力和修正前、后岩石弹性模量间关系，结果表明，不同深度实测水平最大主应力大小与修正前后岩石弹性模量之间均成正相关关系，相关性系数均大于对应的显著性检验临界值，表明两者之间确实存在正相关关系；水平最大主应力和修正后的岩石弹性模量间的相关性较水平最大主应力与修正前的岩石弹性模量间的相关性系数略高，这也在一定程度上反映了岩体结构在地应力与岩石弹性模量关系研究中的作用。

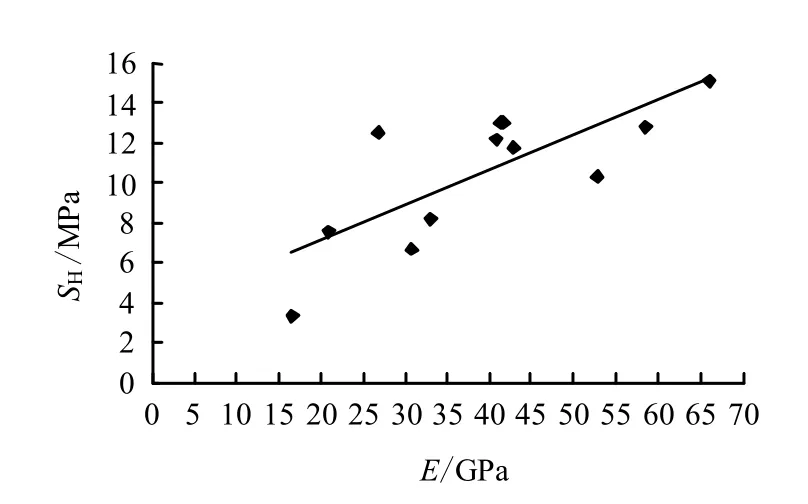
图4 花岗岩中SH -E 关系图 Fig.4 Relation between SH and E in granite

图5 花岗岩中SH -Em关系图 Fig.5 Relation between SH and Em in granite

表4 花岗岩中SH与E 及Em拟合方程及相关性系数 Table 4 Fitting equation & relative coefficient between SH and E (Em) in granite

图6、7 及表5 给出了花岗岩中水平最小主应力和修正前、后岩石弹性模量间关系，表明钻孔中不同深度实测水平最小主应力大小与修正前、后岩石弹性模量之间同样也均成正相关关系，相关性系数均大于对应的显著性检验临界值；水平最小主应力与修正后岩石弹性模量间的相关性较水平最大主应力与修正前岩石弹性模量间的相关性系略高；水平最小主应力与岩石弹性模量间相关性系数比水平最大主应力与岩石弹性模量间相关性系数略高，其原因和意义需进一步研究。

图6 花岗岩中Sh -E 关系图 Fig.6 Relation between Sh and E in granite

图7 花岗岩中Sh-Em关系图 Fig.7 Relation between Sh and Em in granite

表5 花岗岩中Sh与E 及Em拟合方程及相关性系数 Table 5 Fitting equation&relative coefficient between Sh and E(Em) in granite

与花岗岩中地应力与岩石弹性模量表现出的关系不同的是，灰岩中主应力大小与岩石弹性模量间的关系并不十分确定，初步拟合的相关性系数远低于显著性检验临界值，因此，对于灰岩中地应力与岩石弹性模量间关系需要进行更进一步的研究，图8～11 只给出了主应力与岩石弹性模量的散点图，作为对比之用。

图8 灰岩中SH -E 关系图 Fig.8 Relation between SH and E in limestone

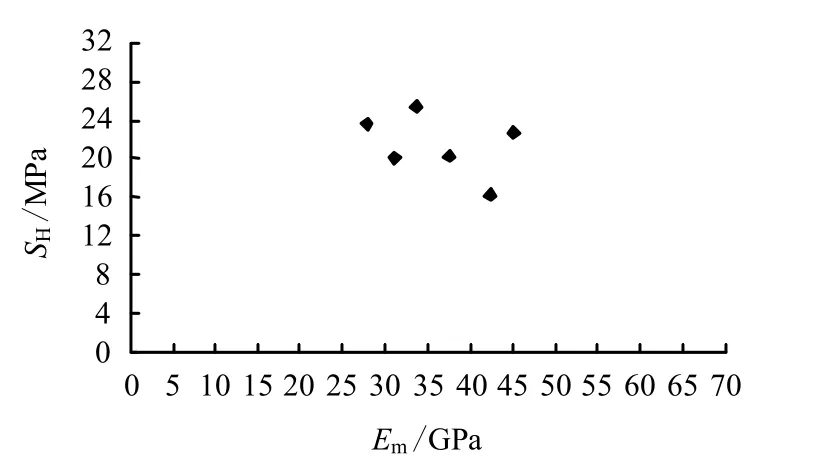
图9 灰岩中SH -Em关系图 Fig.9 Relation between SH and Em in limestone

图10 灰岩中Sh -E 关系图 Fig.10 Relation between Sh and E in limestone

图11 灰岩中Sh-Em关系图 Fig.10 Relation between Sh and Em in limestone

4 初步结论与认识

（1）花岗岩中，主应力大小与岩石弹性模量关系呈正相关关系，并且主应力大小与修正后弹性模量间的相关性系数高于主应力大小与修正前岩石弹性模量间的相关性系数。

（2）灰岩中，主应力大小与岩石弹性模量的关系不明确，需要进一步深入研究。

（3）对比花岗岩和灰岩中主应力大小与岩石弹性模量的关系的分析结果认为，各向同性高的岩体（如花岗岩），实测地应力大小与岩石力学性质试验结果相关性好；而各向异性大的岩体（如沉积岩），实测地应力大小与岩石力学试验结果相关性差，并需要进一步的研究。

（4）地应力与岩石力学性质关系受众多因素的影响，关系十分复杂，本文在前人研究成果的基础上对地应力与岩石力学性质间关系研究进行了一些新尝试，取得了一些新认识。如何准确获得地应力测量深度处岩体力学性质，进行地应力与岩体力学性质间关系定量分析，是后续研究的一个重要内容。

[1] 谢富仁， 邱泽华， 王勇， 等. 我国地应力观测与地震预报[J]. 国际地震动态， 2005， 317(5)： 54－59. XIE Fu-ren， QIU Ze-hua， WANG Yong， et al. Earth stress observation and earthquake prediction[J]. Recent Developments in World Seismology， 2005， 317(5)： 54－59.

[2] 孙叶， 谭成轩. 区域地壳稳定性定量化评价[M]. 北京： 地质出版社， 1998.

[3] 陈庆宣， 王维襄， 孙叶， 等. 岩石力学与构造应力场[M]. 北京： 地质出版社， 1998.

[4] 孙叶， 谭成轩， 孙炜锋， 等. 煤瓦斯突出研究方法探 索[J]. 地质力学学报， 2007， 13(1)： 7－14. SUN Ye， TAN Cheng-xuan， SUN Wei-feng， et al. An approach to the study of coal and gas outburst[J]. Journal of Geomechanics， 2007， 11(1)： 17－14.

[5] 谭成轩， 孙叶， 王连捷. 地应力测量值得注意的若干问题[J]. 地质力学学报， 2003， 9(3)： 275－280. TAN Cheng-xuan， SUN Ye， WANG Lian-jie. Some problems of in-situ crustal stress measurements[J]. Journal of Geomechanics， 2003， 9(3)： 275－280.

[6] 谭成轩， 孙玮烽， 孙叶， 等. 地应力测量及其地下工程应用的思考[J]. 地质学报， 2006， 80(10)： 1627－1632. TAN Chen-xuan， SUN Wei-feng， SUN Ye， et al. A consideration on in-situ crustal stress measuring and its underground engineering application[J]. Acta Geologica Sinica， 2006， 80(10)： 1627－1632.

[7] 白世伟， 李光煜. 二滩水电站坝区岩体应力场研究[J]. 岩石力学与工程学报， 1982， 1(1)： 45－56. BAI Shi-wei， LI Guang-yu. Study on stress field of Ertan hydroelectric station[J]. Chinese Journal of Rock Mechanics and Engineering， 1982， 1(1)： 45－56.

[8] 朱焕春， 陶振宇. 不同岩石中地应力分布[J]. 地震学报， 1994， 16(1)： 49－63. ZHU Huan-chun， TAO Zhen-yu. The distribution of the in-situ stress in different rocks[J]. Acta Seismologica Sinica， 1994， 16(1)： 49－63.

[9] 景锋， 盛谦， 张勇慧， 等. 不同地质成因岩石地应力分布规律的统计分析[J]. 岩土力学， 2008， 29(7)： 1877－1883. JING Feng， SHENG Qian， ZHANG Yong-hui， et al. Statistical analysis of geostress distribution laws for different rocks[J]. Rock and Soil Mechanics， 2008， 29(7)： 1877－1883.

[10] 赵德安， 陈志敏， 蔡小林， 等. 中国地应力场分布规律统计分析[J]. 岩石力学与工程学报， 2007， 26(6)： 1265－1271. ZHAO De-an， CHEN Zhi-min， CAI Xiao-lin， et al. Analysis of distribution of geostress in China[J]. Chinese Journal of Rock Mechanics and Engineering， 2007， 26(6)： 1265－1271.

[11] ZOBACK M D， TSUKARA H， HICKMAN S. Stress measurements at depth in the vicinity of the San Andreas fault-implications for the magnitude of shear stress at depth[J]. J. Geophys. Res.， 1980， 85： 6157－6173.

[12] EVANS K F. Appalachian stress study. Regional scale stress variations and their relation to structure and contemporary tectonics [J]. J. Geophys. Res.， 1989， 94： 17619－17645.

[13] MARTIN C D. Characterizing in-situ stress domains at the AECL underground research laboratory[J]. Canadian Geotechnical Journal， 1990， 27： 631－646.

[14] 苏生瑞， 黄润秋， 王士天. 断裂构造对地应力场的影响及其工程应用[M]. 北京： 科学出版社， 2002.

[15] 陈群策， 李方全. 对地应力尺寸效应的讨论[C]//谢富仁， 陈群策， 崔效锋， 等编. 中国大陆地壳应力环境研究. 北京： 地质出版社， 2003.

[16] 蔡美峰， 王双红. 地应力状态与围岩性质的关系研 究[J]. 中国矿业， 1997， 6(6)： 38－41. CAI Mei-feng， WANG Shuang-hong. Relation between ground stress behavior and properties of surrounding rock[J]. China Mining Magazine， 1997， 6(6)： 38－41.

[17] AITMATOV I T， VDOVIN K D， KOJOGULOV K C H， et al. State of stress in rock and rock-burst in Seismicactive folded areas [DB/OL]. Canada： International Society for Rock Mechanics [1987-08-30]. http：//www.onepetro.org/mslib/servlet/onepetropreview?i d=ISRM-6CONGRESS-1987-139

[18] 韩嵩. 深部地应力环境对砂岩力学性质的影响[J]. 矿业研究与开发， 2007， 27(2)： 16－31. HAN Song. The influences of deep in-situ stress field on mechanical properties of sandstone[J]. Mining Research and Development， 2007， 27(2)： 16－31.

[19] HAIMSON B C， CORNET F H. ISRM suggested methods for rock stress estimation—Part 3： Hydraulic fracturing (HF) and/or hydraulic testing of pre-existing fractures (HTPF)[J]. International Journal of Rock Mechanics & Mining Sciences， 2003， (40)： 1011－1020.

[20] 陈彭年， 陈宏德， 高莉青. 世界地应力实测资料汇 编[M]. 北京： 地震出版社， 1990.

[21] 尤明庆， 苏承东. 层理倾角不同的砂岩变形破坏和强度的研究[J]. 河南理工大学学报（自然科学版）， 2009， 28(5)： 626－635. YOU Ming-qing， SU Cheng-dong. Study on the deformation， failure and strength of sandstone with various declined bedding[J]. Journal of Henan Polytechnic University (Natural Science)， 2009， 28(5)： 626－635.

[22] 尤明庆. 岩石试样的杨氏模量与围压的关系[J]. 岩石力学与工程学报， 2003， 22(1)： 53－60. YOU Ming-qing. Effect of confining pressure on the Young’s modulus of rock specimen [J]. Chinese Journal of Rock Mechanics and Engineering， 2003， 22(1)： 53－60.

[23] 曹庆林， 周慧. 节理岩体变形特性的参数研究及等效弹模的数值确定[J]. 冶金矿山设计与建设， 1996， (2)： 3－7. CAO Qing-lin， ZHOU Hui. Numerically determining the equivalent modulus of jointed rock mass based on the parametric study on its compressibility[J]. Metal Mine Design and Construction， 1996， (2)： 3－7.

[24] HUANG T H， CHANG C S， YANG Z Y. Elastic modulus for fractured rock mass[J]. Rock Mechanics and Rock Engineering， 1995， 28(3)： 135－144.