中国经济增长中的环保投资贡献的实证分析
2012-01-07刘继红张大伟
徐 辉,刘继红,张大伟,高 毅
(1.兰州大学1a经济学院,1b.干旱与草地生态教育部重点实验室,兰州730000;2.黄委上游水文水资源局,兰州730030)
0 引言
近年来随着我国经济的快速增长,环境污染问题越来越严重,成为影响甚至制约经济增长的重要因素,环境污染已日益成为制约我国经济发展的“瓶颈”。
国内学者分别采用了不同的计量经济学方法对我国的环保投资与经济增长之间的关系进行了大量研究,但总体来看还存在着以下问题:(1)一些研究所采用的时间序列数据样本较小,在进行E--G两步法分析环保投资与经济增长之间的协整性与因果关系时可能造成参数估计的误差较大。(2)一些研究没有考虑误差修正对Granger因果关系的影响。(3)很多研究在建立C--D生产函数的过程中,对于劳动力这一因素没有考虑其质量的变化。(4)一些研究忽略了技术进步对于经济增长的贡献,这与现实情况并不相符。
因此,本文以C--D生产函数为基础,运用我国1990~2009年近20年的统计数据,采用VAR模型下的JJ协整检验法,检验变量之间的协整关系,并建立长期协整关系及误差修正模型,进而寻求GDP、劳动力、经济建设投资、环保投资以及TFP全要素之间的函数关系。
1 模型的构建
1.1 经济增长的影响因素分析与C—D生产函数
GDP用来衡量经济产出,在生产函数中常以Y表示。经济产出Y的影响因素主要包括:劳动投入(L)、经济建设投入(K)、环保投入(H)以及综合衡量知识与科技进步、产业结构与制度等因素的全要素生产率(TFP)。纳入环保投入与全要素生产率的C—D生产函数可表述为:

其中,Y(t)、K(t)、L(t)、H(t)分别为GDP、经济建设投资、劳动力和环保投资指标;β、β、θ分别是经济建设投资、劳动力投入和环保投资指标的弹性系数;A0为基年的TFP全要素值,γ是TFP全要素的平均增长率。
此处假设存在Hicks技术进步中性,即经济增长的规模报酬不变则α+β+θ=1,则而将β=1-α-θ代入式(1)同时除以L(t)并取自然对数可得:

式(2)对时间t求导得:

其中gy、gk、gh分别代表劳动力平均GDP与劳动力平均经济建设投资与劳动力平均环保投资的增长率。
由公式(3)可知,在纳入环保投资和规模报酬不变的情况下,劳动力平均GDP的变化包括:TFP全要素的增长率,劳动力平均经济建设投资及劳动力平均环保投资的变化乘以各自的权重。
1.2 参数的确定及数据来源
本文时间序列数据来源均为相应年份的《中国统计年鉴》
(1)GDP:采用1990~2009年我国GDP历年统计结果,并折合为1999年的不变价格。
(2)K(t):由于相关的数据比较难收集,因此这里使用全社会固定资产投资总额代表经济建设资金,并折合为1999年的不变价格。
(3)L(t):本文的劳动力L使用历年统计的全社会职工工资总额,而非传统方法采用的历年从业人员总计,原因是前者包含着经济发展以及劳动力质量变化等因素。应用时以1999年为基期,折算成以1999年为不变价格的职工工资总额(如图1)。
(4)H(t):环境污染治理投资是环保投资的主要部分,根据数据的可获得性,本文中环保投资数据用环境污染治理投资数据代替,并采用历年统计的并折合为1999年的不变价格(如图2)。

图1 1990~2009年我国GDP、全社会职工工资总额、经济建设投资总额变化曲线
2 数据统计与模型的实证分析
2.1 统计数据的处理及平稳性检验
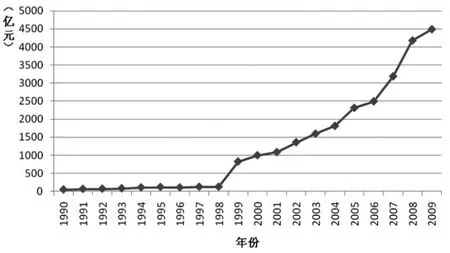
图2 1990~2009年我国环保投资变化曲线
为了避免模型的“虚假回归”或“伪回归”的问题,要求各时间序列的变量具有同阶平稳性且相互之间具有协整关系。首先需对时间序列Lny、Lnk、Lnh进行单位根检验,本文采用ADF单位根检验方法。在ADF检验过程中最优滞后阶数选取的原则为:在保证残差不相关的前提下,AIC值或SC值越小越好,本文采用AIC准则。ADF检验结果如表1所示:
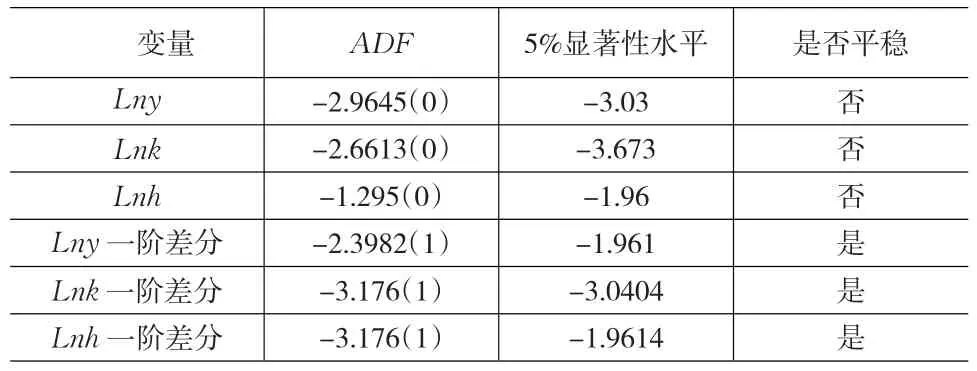
表1 变量平稳性ADF单位根检验结果
由表1可见,时间序列变量Lny、Lnk、Lnh的非平稳性比较显著,但一阶差分全都是平稳的。
2.2 VAR模型与变量协整分析
在确定了时间序列变量Lny、Lnk、Lnh同阶平稳性后,通过协整分析来判断三个变量之间是否存在协整关系,能排除“虚假回归”或“伪回归”问题的可能性,本文运用基于回归系数的JJ检验法。在采用JJ检验法进行协整分析之前,先构建Lny、Lnk、Lnh的向量自回归模型VAR。在构建模型中滞后阶数的选取尤为重要,确定时要综合考虑LogL、LR统计量、FDE(最终预测误差)、AIC信息准则、SC信息准则、HQ信息准则。运用Eviews6.0建立VAR模型并进行滞后阶数的选取(见表2),可知LR、FDE、AIC、SC、HQ均指向1阶滞后。因此,本文选取1阶滞后(见表2)。

表2 VAR模型滞后阶数的选取
为准确地确定VAR模型的滞后阶数,还需对VAR模型进行滞后排除检验(见表3),可知内生变量Lny、Lnk、Lnh的第一阶滞后χ2统计量分别为7.487764、10.44207、8.739941,相应的概率P值为0.04787、0.015159、0.032956,在5%的显著性水平下,都通过了显著性检验,从而说明在VAR模型中,Lny、Lnk、Lnh所有的滞后内生变量是联合显著的。第一阶滞后和Joint所在元素的χ2统计量=35.40513,相应的概率值=5.05e-05,在5%的显著性水平下,通过显著性检验。因此,VAR模型选取一阶滞后(见表3)。

表3 VAR模型滞后排除检验
之后进行内生变量的协整检验,根据式(2)协整方程应包含截距项且有线性趋势。在此前提下,将检验的滞后阶数选取为1阶,则基于VAR模型的JJ协整检验结果。
可知,在“存在零个协整关系”的原假设下,迹统计量=41.46278,5%的临界值=35.01090,迹统计量大于临界值,因此拒绝原假设,从而表明至少存在一个协整关系。在“至多1个协整关系的”的原假设下,迹统计量=13.96667,5%的临界值=18.39771,迹统计量小于临界值,因此不能拒绝原假设,进而表明在5%显著性水平上存在一个协整关系。无论是迹检验还是最大特征值检验,都表明在5%的显著性水平下,拒绝原假设,即拒绝没有协整方程的零假设,支持存在1个协整方程的假设。也就是说内生变量Lny与内生变量Lnk、Lnh之间存在长期的均衡关系,并且这种关系具有线性趋势。
2.3 Granger因果关系检验
由于Lny与Lnk、Lnh之间存在长期的均衡关系,则各个变量之间必然存在Granger因果关系。然而对于非平稳变量之间存在协整关系,首先要通过差分的方法使变量达到平稳,但是在这一过程中会在一定程度上消除长期趋势,因此在VAR模型中的Granger因果关系检验只包含短期趋势,而得出的结论会有一些误差。因此本文采用基于VCEM的Granger因果关系检验。首先建立Lny、Lnk与Lnh的VCEM模型,检验的滞后阶数为1,确定性趋势的选定应包含截距项且有线性趋势,模型的估计结果如下:

从图3可以看出,零值均线代表了变量之间的长期均衡稳定关系。在1999年,误差修正项的值比较大,表明在该时期短期波动偏离长期均衡关系比较大,经过两年的调整,又回到了长期均衡稳定状态。之后误差修正项的数值比较小,短期波动偏离长期均衡的幅度比较小(见图 3)。

图3 VEC模型的协整关系图
基于VECM的短期Granger因果关系检验,在Eviews6.0中实现,如表4所示:

表4 基于VECM的短期Granger因果关系检验
由表4可见,D(Lnk)是D(Lny)的单向Granger原因,D(Lny)是 D(Lnh)的单向 Granger原因,D(Lnk)不是 D(Lnh)的单向 Granger,D(Lny)与 D(Lnh)均不是 D(Lnk)的Granger原因。也就是说短期中经济建设投资是GDP的单向原因,而环保投资不是GDP的单项原因,GDP反而是环保投资的单项原因。

表5 基于VECM的长期Granger因果关系检验
由表5可见,D(Lny)与D(Lnh)的误差修正项系数在1%水平下是显著的,表明1%显著性水平下所选变量均是D(Lny)与D(Lnh)的长期原因;D(Lnk)的误差修正项系数在5%水平下是显著的,表明5%显著性水平下所选变量均是D(Lnk)的长期原因。由此可以认为,GDP、经济建设投资和环保投资两两之间均存在着双向长期Granger因果关系。当变量之间同时具有短期与长期因果关系时,称之为强因果关系。综合短期与长期的Granger因果关系检验发现,经济建设投资与GDP存在着强单向Granger因果关系,而且为从前者指向后者;而GDP与环保投资之间存在着强单向Granger因果关系,为前者指向后者。

表6 时间变量回归结果
2.4 回归与实证分析
以(2)式为基础,对时间序列进行回归,结果如表6所示。
即回归方程为:

由R2值可判断,回归方程的拟合优度能满足分析的要求,F统计量下的P值很小,说明方程在整体上是显著的。对单个解释变量Lnh的P值=0.0977,在10%的显著性水平下,可以拒绝系数不显著的原假设。虽然Lnk的系数不显著,但可以作为综合分析的参考。
由回归方程可知,经济建设投资的弹性系数α=0.029014,环保投资的弹性系数θ=0.005896,故劳动力的弹性系数β=0.96509。在这20年中,考虑到在长期均衡情况下,GDP与环保投资之间存在着双向的Granger原因,而短期内GDP是环保投资的单向Granger原因,可以认为我国的环保投资短期内是由于经济增长带动的,长期内又反过来影响经济的增长,但是其对经济增长的贡献度比较小。包含了技术进步、产业结构与制度等因素的全要素TFP年均增长率为1.4652%。说明了全要素TFP对我国经济增长有着正的作用,因此在环保过程中,要提高技术水平,合理调整产业结构。
2.5 脉冲响应分析与方差分解
VAR模型把系统中每一个内生变量作为系统中所有内生变量的滞后项的函数来构造。本文利用VAR模型建立脉冲响应函数能够描述对一个扰动项的一个标准差冲击对模型中所有内生变量当前值和未来值的影响。而方差分解分析每个信息冲击对内生变量变化的贡献度,从而了解各信息对模型内生变量的相对重要性。本文以劳动力平均GDP增长率gy、劳动力平均经济建社投资增长率gk、劳动力平均环保投资增长率gh为内生变量建立VAR模型,并进行脉冲响应分析和方差分解,VAR模型的滞后阶数选取为1阶。
在脉冲响应分析之前,要对gy、gk、gh建立的VAR模型进行稳定性检验以确保脉冲响应标准误差的有效性。先给出VAR模型的AR的特征多项式根的图,如图4所示。由图4可知所有根的倒数的模都小于1,并且位于单位圆之内,因此所构建的VAR模型是平稳的。
之后对VAR模型进行脉冲响应分析,重点关注gy对加在gk、gh之上的冲击的脉冲响应(见图5)。
从图5中可以发现,当gk、gh受正冲击时,两者都会对gy产生负面影响,并且这种影响第2年达到最大,之后逐渐减小,在16-17年后基本趋近与零。这一结论看似与新古典经济增长理论中的单位人均资本投入越多,产出越多的观点相矛盾,但在这我们仔细分析gy、gk、gh的含义不难发现:本文中gy、gk、gh分别代表劳动力平均GDP与劳动力平均经济建设投资与劳动力平均环保治理投资的变化率,与新古典经济增长理论中的人均产量,和人均资本意义不同。对gk、gh的正冲击,可理解为经济建设投资和环保投资的增长率均高于全社会职工工资的增长率。对全社会而言,能够使劳动者工资增长的经济建设投资和环保投资的投入成本均增加了。对gy的负影响可以理解为GDP的增长率小于全社会职工工资的增长率,而对于全社会而言,其GDP增长的劳动成本升高了。由此可见,经济建设投资和环保投资的增长相对过快,而劳动者工资的增长没有跟上,将会致使劳动的产出效率下降或者对GDP增长的劳动成本相应提高。
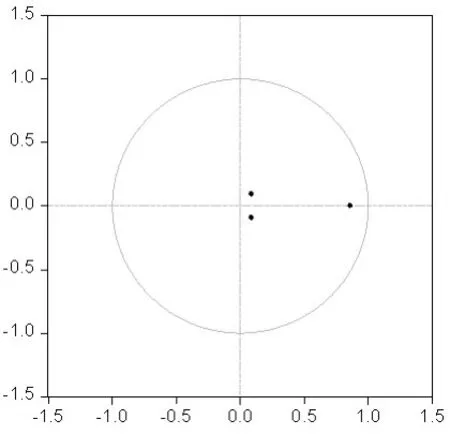
图4 VAR模型的AR根
对VAR模型进行方差分解,重点关注gk、gh的变化对gy的方差分解(表7)。gy列是劳动力平均GDP变化率预测方差中由自身引起的部分的百分比;gk列是劳动力平均GDP变化率预测方差中由平均经济建设投资变化率引起的部分的百分比;gh列是劳动力平均GDP变化率预测方差中由环保投资变化率引起的部分的百分比;这三列的百分比之和为100。可见,在不考虑gy对自身变化贡献率的前提下,gk、gh对gy的贡献率随着时间的推移越来越大,其中gk对gy的贡献较大。

图5 gy对各内生变量冲击的脉冲响应
3 结论与建议
根据上述分析可见,我国经济增长与环保投资之间存在明显的均衡关系,但目前后者对前者的弹性系数比较小。基于VECM的Granger因果关系检验表明,短期内GDP是环保投资的单向Granger原因,而GDP、经济建设投资,环保投资两两之间存在双向长期Granger因果关系。总的来说环保投资短期内对我国经济增长的贡献不是很大,但是长期而言对我国经济增长的贡献将逐渐增大,这也符合目前我国经济发展中的对环境问题逐渐重视的发展阶段。
综合以上结论,本文提出以下建议:(1)进一步加大科技研发、制度与管理模式优化和创新的力度,增加全要素生产率对我国经济增长的贡献。(2)大力推进产业结构的调整与升级,加大环保投资的力度,建立大型骨干企业,提高其专业性水平,减少低水平的重复建设。(3)调整我国经济发展模型中劳动力投资增幅过大的模式,多关注民生和福利问题,保持经济建设投资、环保投资与劳动者工资增速的协调和同步,这对我国经济的稳定持续增长具有积极的意义。
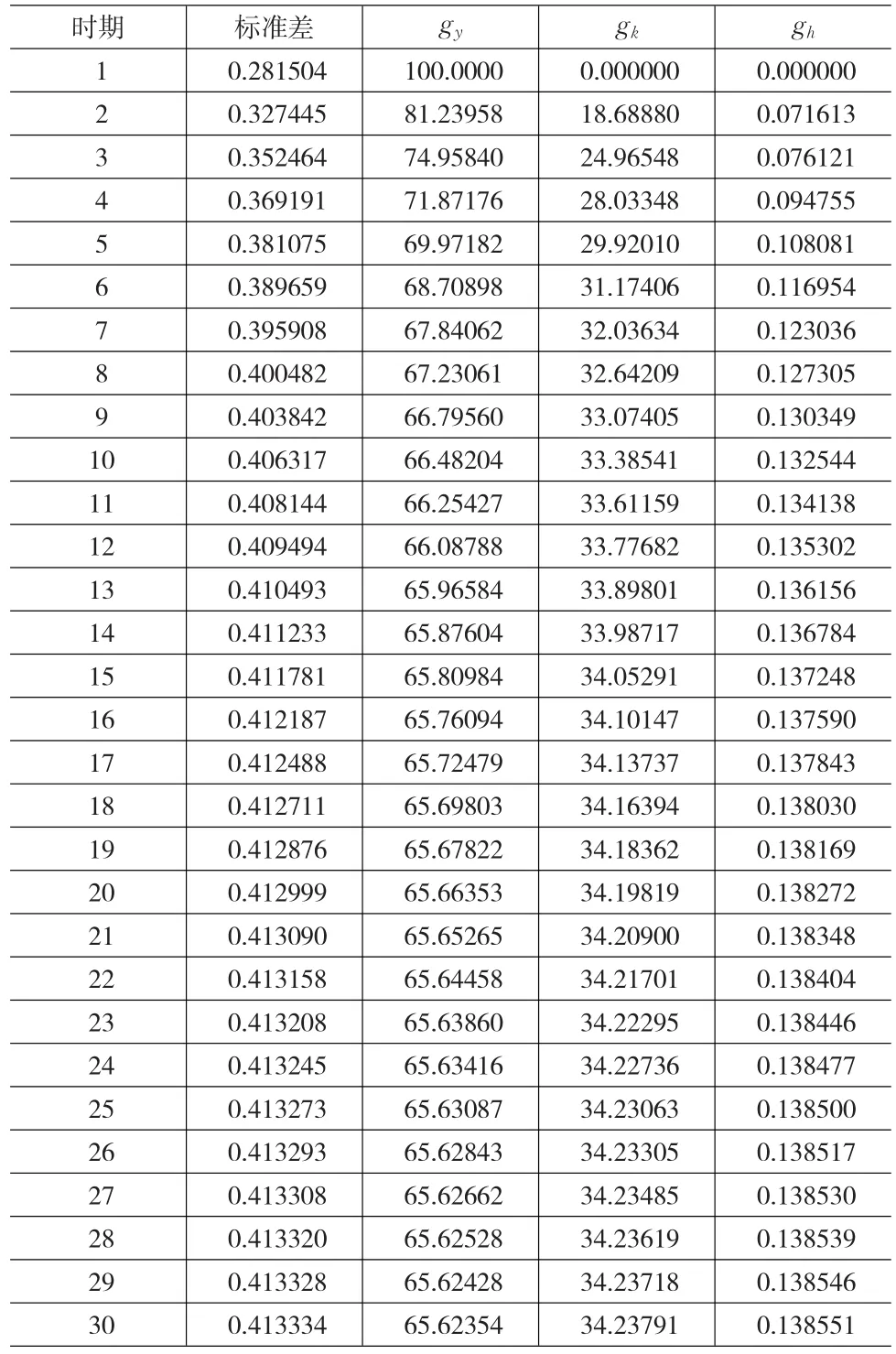
表7 gy对各内生变量变化的方差分解表
[1]Gentry B S L.Fernandez.Evolving Public-Private Partnership:Gener⁃al Themes and Examples Les from the Urban Water Sector[M].Paris:OECD,1998.
[2]新饭田宏.投入产出分析入门[M].北京:中国统计出版社,1990.
[3]厉以宁,章铮.环境经济学[M].北京:中国计划出版社,1995.
[4]徐嵩龄.中国环境破坏的经济损失计量:实例与理论研究[M].北京:中国环境科学出版社,1998.
[6]胡海青,李建,张道宏.环保投资与经济增长的协整及因果关系检验[J].科技进步与对策,2008,(7).
[7]雷社平,何音音.我国环保投资与经济增长的回归分析[J].西北工业大学学报,2010,(2).
[8]邵海清.环保投资与国民经济增长的灰色关联分析[J].生产力研究,2010,(12).
[9]高铁梅.计量经济分析方法与建模[M].北京:清华大学出版社,2010.
