关于函数的单叶性及判别函数单叶性的几种方法

阿布力米提·米吉提

(伊犁师范学院 数学系，新疆 伊宁 835000)

1 预备定义和定理

1.1 关于几何函数论与单叶函数

几何函数论(也称复变函数几何理论)，它的理论和方法不但可以用来解决微分方程、解析数论、微分几何、拓扑学等许多数学分支提出的问题，而且更为普遍地应用于自然科学的诸多领域[1-2].单叶函数是几何函数论的重要内容之一.

定义1 设D={z;|z|<1}表示单位圆盘，函数f(z)是在区域D全纯.

定理1 若f(z)在z=z0全纯，且f′(z0)≠0，则存在δ>0，f(z)在|z-z0|<δ单叶.

1.2 关于从属理论与从属原理

从属理论是几何函数论中的一个重要部分，应用它研究单叶函数的各种几何性质是很方便的[3-4].再说，一方面从属原理本身就有交明确的几何性质.另一方面，从属原理最大的优势就是把两个全纯的函数通过一个特殊的全纯函数有机地联系在一起.这个特殊函数是区域D中全纯且影射D到自身、原点对应原点的函数的全体所组成的函数族.

也就是，记:H(D)={f(z);/f(z)在D中全纯}，B={φ(z);/φ(z)∈H(D)且|φ(z)|<1}，

P={P(z);/P(z)∈H(D),ReP(z)>0}.

定义2 设f(z)∈H(D),g(z)∈H(D)，若存在φ(z)∈B,且φ(0)=0,使f(z)=g(φ(z))，称f(z)在区域D从属于g(z,)记为f(z)g(z).

若f(z)g(z)，有φ(D)⊂D,φ(0)=0,从而由从属的定义推出f(D)⊂g(D),且f(0)=g(0).

定理2 设g(z)在D中单叶，则f(z)g(z)当且仅当f(0)=g(0)且f(D)⊂g(D).

证明“⟹” 由于f(z)g(z)，有φ(D)⊂D,φ(0)=0,从而由从属的定义推出f(D)⊂g(D),且f(0)=g(0).

“⟸” 由于g(z)在D中单叶的，故g-1(w)在g(D)中全纯且单叶，若f(D)⊂g(D)，则令g(z)=g-1(f(z))∈B，且由f(0)=g(0)得到φ(0)=0,显然对这样的g(z)有f(z)=g(φ(z)).证毕.

关于核函数与从属链以及变系数线性微分方程组的有关记号、定义及定理见文献[5-8].

2 判断函数f(z)单叶函数的几种方法

定理3 设f(z)在z=z0全纯，且f′(z0)≠0，若:

(1)

则f(z)在D中单叶.

定理4 若f(z)在D全纯函数，且f′(z0)≠0，φ(t)是[0,1]上的可微复值函数，且φ(1)=0,φ(x)-xφ′(x)≠0,x+φ(x)≠0,令|z|=r,若f(z)满足：

(2)

则f(z)是D中的单叶函数.

证明不妨设f(z)=z+a2z2+…，考虑函数:L(z,t)=f(e-tz)+φ(e-t)zf′(e-tz),t≥0，则:

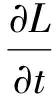
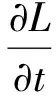
此时：

从而:

由最大模原理:

故令u=e-tξ0,则|u|=e-t<1,即u∈D，

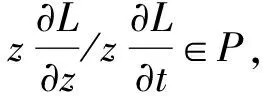
故通过对L(z,t) 的标准化后由定理2知L(z,t) 是从属链，从而当t≥0时，L(z,t) 在D中单叶.

特别注意：φ(1)=0便知L(z,0)=f(z)在D中单叶.

推论1 若f(z)在D全纯函数，且f′(z0)≠0，φ(t)是[0,1]上的可微复值函数，且φ(1)=0,φ(x)-xφ′(x)≠0,x+φ(x)≠0,令|z|=r,若f(z)满足:

(3)

则f(z)+(c-1)zf′(z)在D中单叶.

如果定理4中令：φ(r)=r-β-rβ，可得:

推论2 若f(z)在D全纯函数，且f′(z0)≠0，φ(t)是[0,1]上的可微复值函数，且φ(1)=0,φ(x)-xφ′(x)≠0,x+φ(x)≠0,令|z|=r,若f(z)满足:

(4)

其中r=|z|<1.

则函数f(z) 在D中单叶.

如果定理4中令：φ(r)=r-β-1，可得:

推论3 若f(z)在D全纯函数，且f′(z0)≠0，φ(t)是[0,1]上的可微复值函数，且φ(1)=0,φ(x)-xφ′(x)≠0,x+φ(x)≠0,令|z|=r,若f(z)满足:

其中r=|z|<1,

(5)

则函数f(z) 在D中单叶.

如果定理4中令：φ(r)=r-β-r，可得:

推论4 若f(z)在D全纯函数，且f′(z0)≠0，φ(t)是[0,1]上的可微复值函数，且φ(1)=0,φ(x)-xφ′(x)≠0,x+φ(x)≠0,令|z|=r,若f(z)满足:

其中r=|z|<1,

(6)

则函数f(z) 在D中单叶.

特别在式(5)与式(6)中取β=1与β=2时分别可得一下两个结果：

推论5 若f(z)在D中的全纯函数且f′(z0)≠0，若:

则f(z)是D中的单叶函数.

推论6 若f(z)在D中的全纯函数且f′(z0)≠0，若:

则f(z)是D中的单叶函数.

定理5 若f(z)在D中的全纯函数且f′(z0)≠0，φ(t)与定理6中相同，r=|z|，且:

(7)

则f(z)是D中的单叶函数.

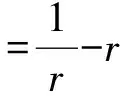
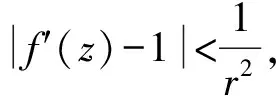
利用微分方程的方法也可得到一些单叶性判别的准侧.

定理6 设f(z)在D内局部单叶，即f′(z)≠0,(z∈D)，定义:

(8)

则f(z)在D中单叶的充要条件是二阶线性微分方程:

w″(z)+v(z)w(z)=0.

的每个非平凡解在D内至多有一个零点.

推论8 设f(z)在D内局部单叶，即f′(z)≠0,(z∈D)，定义：

(9)

wi″+v(z)wi=0(i=1,2)

(10)

的每个非平凡解在D内至多有一个零点.

证明(在下面只证当i=1时的情况).

(11)

且具有一般解u(z)=αf(z)+β，但方程(1)的每个非平凡解在D中至少有一个零点的充要条件是f(z)在D中单叶，故当i=1时，定理结论成立.(同样可证，当i=2时的情况)

定理7 设p(x)是实值的偶函数，在x∈(-1,1)内连续且当x∈(-1,1)时, (1-x2)p(x)单调递减，若：

(12)

具有一个解u(x)>0，且f(z)在D中局部单叶，由式(18)是对应的v(z)满足：

|v(z)|≤p(|z|), (z∈D),

(13)

则f(z)在D中单叶.

[1] 阿尔福斯.复分析[M].张立，张靖译.上海:上海科技出版社，1984.

[2] 戈鲁辛.复变函数几何论[M]. 陈建功译.北京:科学出版社，1956.

[3] 高建福.单位圆盘内正则函数的单叶性准则[J].数学的实践与认识，1999(29):165-168.

[4] 高建福.正则函数的从属性与单叶性[J].亚洲教育，2003,7(1):60-61.

[5] 范春方.某些一阶微分方程解析解的单叶性[J].数学学报，1992,35(4):483-491.

[6] E.卡姆克.常微分手册[M].张鸿林译.北京:科学出版社,1977.

[7] 贝尔曼.微分方程解的稳定性理论[M].北京：科学出版社，1957.

[8] 邓宗琦.二阶线性齐次微分方程的注记[J].华中师院学报,1983(2):7-12.

[9] 阿布力米提.几类变系数线性微分方程组的可解型[J].伊犁师院学报,2006(3)：30-33.