Gram矩阵在不等式中的应用
2012-01-05张宾
张 宾
(湖北民族学院 预科教育学院,湖北 恩施 445000)
定义1[1]设x1,x2,…,xn是内积空间中的n个向量,矩阵:
称为由x1,x2,…,xn生成的Gram矩阵.通常用G(x1,x2,…,xn)来记上述Gram矩阵.其行列式称为Gram行列式,通常用Γ(x1,x2,…,xn)表示.
引理1[5]设x1,x2,…,xn是内积空间中的n个向量,则G(x1,x2,…,xn)为半正定矩阵,当且仅当x1,x2,…,xn线性无关时G(x1,x2,…,xn)为正定的.
引理2 设x,y,z是实内积空间中的三个非零向量,则:
式(1)当且仅当x1,x2,…,xn线性相关时等号成立.
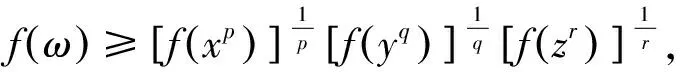
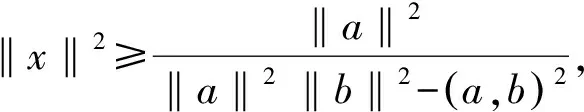
定理1 设x,y是实内积空间中的向量,若x=(ξ1,ξ2,…,ξn),y=(η1,η2,…,ηn),则有:
其中1≤i≤n.

(1)

定理2 设f,g是区间(a,b)上的Lebesgue可积函数,满足:
m≤f(x)≤M,n≤g(x)≤N,∀x∈(a,b),其中m+M≠0,n+N≠0,则有:

整理得: |‖g‖2(f,1)-(f,g)(g,1)|≤
‖f‖dist(g,Span{f})dist(g,Span{1})≤‖g‖dist(f,Span{g})dist(g,Span{1}).
代入得:
‖f‖dist(g,Span{f})dist(g,Span{1})≤
(b-a)2‖g‖dist(f,Span{g})dist(g,Span{1})
由题设m≤f(x)≤M,n≤g(x)≤N,∀x∈(a,b)得:

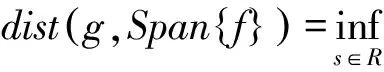





综上可得结论:
定理3 设x1,x2,…,xn为内积空间中的向量,‖xi‖≤1,则有:

证明因为Γ(x1,x2,…,xn)≤Γ(x1)Γ(x2)…Γ(xn).
由Gram矩阵的性质知,这些行列式都非负且小于等于1,所以:
Γα(x1,x2,…,xn)≤Γα(x1)Γα(x2)…Γα(xn),其中α≥0,
注:同理可得下面结论.
定理4 设x1,x2,…,xn为内积空间中的向量,‖xi‖≤1,1≤k≤n,则有:

根据引理4(Ostrowski不等式)[2]和引理2可得以下结论:
定理5 设a,b,x是实内积空间的三个非零向量,满足(a,x)=0,‖x‖=1,则有:

证明在式(1)中用a,b,x代替式(1)中的x,y,z得:
因为(a,x)=0,‖x‖=1,故(a,b)2≤‖a‖2[‖b‖2-(b,x)2],

设x=λa+μb,由假设条件(a,x)=0,‖x‖=1可得:
‖a‖2λ+(a,b)μ=0,‖a‖2λ2+2(a,b)λμ+‖b‖2μ2=1,



证明由G(a,b,x)得半正定性得Γ(a,b,x)≥0,即:
展开得:‖a‖2‖b‖2‖x‖2-‖a‖2(b,x)2-‖b‖2(a,x)2-‖x‖2(a,b)2+2(a,b)(a,x)(b,x)≥0.
代入题设条件(a,x)=0,‖x‖=1得:‖a‖2‖b‖2≥‖a‖2(b,x)2+(a,b)2,
由函数性质可得:‖a‖p‖b‖p≥‖a‖p(b,x)p+(a,b)p,p≥2,

证明将Γ(x,a,b,c)展开整理后可得[4]:
‖c‖2Γ(x,a,b)+Q(x,a,b,c)≥ [‖x‖‖a‖|(b,c)|-‖x‖‖b‖|(a,c)|]2+
[‖x‖‖a‖|(〗b,c)|-‖a‖‖b‖|(x,c)|]2+
[‖x‖‖b‖|(a,c)|-‖a‖‖b‖|(x,c)|]2.
其中:Q(x,a,b,c)= ‖x‖2‖y‖2|(z,ω)|2+‖x‖2‖z‖2|(y,ω)|2+‖y‖2‖z‖2|(x,ω)|2-
2(x,ω)(x,y)(z,ω)(y,z)-2(z,ω)(x,z)(x,y)(y,ω)-2(y,ω)(x,z)x(z,ω)(y,z)+
(z,ω)2(x,y)2+(y,ω)2(x,z)2+(x,ω)2(y,z)2
代入题设条件(x,a)=0,(x,b)=1,(x,c)=0得:

定理8 设设x,a,b,c是实内积空间中的向量,满足‖x‖=1,(x,a)=0,(x,b)=0,则有:
证明将Γ(x,a,b,c)展开整理后可得:
‖x‖2Γ(a,b,c)+Q(x,a,b,c)≥[‖a‖‖b‖|(c,x)|-‖a‖‖c‖|(b,x)|]2+
[‖a‖‖b‖|(c,x)|-‖b‖‖c‖|(a,x)|]2+[‖a‖‖c‖|(b,x)|-‖b‖‖c‖|(a,x)|]2.
代入题设条件‖x‖=1,(x,a)=0,(x,b)=0可得:
Γ(a,b,c)+[‖a‖2‖b‖2+(a,b)2](c,x)2≥2‖a‖2‖b‖2(c,x)2,

证明将Γ(y,x1,x2,…,xn)展开得[3]:
‖y‖2[‖x1‖2-btG-1(x2,…,xn)b]Γ(x2,…,xn)-Γ(x2,…,xn)=‖y‖2Γ(x1,x2,…,xn)-Γ(x2,…,xn).


证明将Γ(y,x1,x2,…,xn)展开得:
Γ(y,x1,x2,…,xn)= Γ(x1,x2,…,xn-1)[‖xn‖2-(xn,y)2-btG-1(x1,x2,…,xn-1)b]=
Γ(x1,x2,…,xn-1)[‖xn‖2-btG-1(x1,x2,…,xn-1)b]-Γ(x1,x2,…,xn-1)(xn,y)2=
Γ(x1,x2,…,xn)-Γ(x1,x2,…,xn-1)(xn,y)2[8].
这里b=((x1,xn),(x2,xn),…(xn-1,xn))t.
由Γ(y,x1,x2,…,xn)≥0可得:Γ(x1,x2,…,xn)-Γ(x1,x2,…,xn-1)(xn,y)2≥0,
由Gram矩阵的性质可知当且仅当x1,x2,…,xn,y线性相关时等号成立.
[1] MA J G.An Identity in real Inner Product Spaces[M].Zhizhou:JIPAM,China,2007.
[2] DRAGOMIR S S . A Generralization of Gr¨uss’inequality in inner Product Spaces and Application[J].J Math Anal Appl,1999,237:74-82.
[3] ALI′C M, J. PEˇCARI′C. On some inequalities of ˇZ. Madevski and A. M. Ostrowski [J].RadHAZU,Matematiˇcke znanosti,1997,472:77-82.
[4] BEESACK P R.On Bessel’s inequality and Ostrowski’s [J].Univ Beograd Publ Elektrotehn Fak,Ser Mat Fiz,1975,498/541:69-71.
[5] CHO Y J, MATI′C M, PEˇCARI′C J. On Gram’s determinant in 2-inner product spaces[J].J Korean Math Soc,2001,38(6):1125-1156.
[6] Vlad Ciobotariu-Boer.An Intergral Inequality for 3-convex Function[M].Cluj-Napoca Romania,2000.
[7] Ostrowski A Vorlesungen.Über Differential and Integralrechnung[J].Basel,1951,2:289-294.
