二相编码信号载频盲估计快速算法研究

张刚兵，胥嘉佳

(1.常州工学院电子信息与电气工程学院，江苏 常州 213002；2.南京模拟技术研究所，江苏 南京 210000)

二相编码信号广泛应用于通信和雷达系统.在许多应用领域，需要先对BPSK信号参数进行估计，然后才能解码.其中BPSK信号的载频估计是码速率估计、初始相位估计和同步估计等其它参数估计的基础，载频估计的精度直接影响BPSK解码的正确率.在通信领域中相位编码(MPSK)信号的载频盲估计问题是研究的热点，Veterbi A.J.和Veterbi A.M.[1]提出的前馈最大似然估计算法(V&V算法)，可以对MPSK信号的相位和频偏进行盲估计.以V&V算法为基础得到了一类盲最小二乘频偏估计算法[2-3]，把频偏估计问题转化为估计加性高斯白噪声污染的正弦波频率估计问题，在通信中获得广泛应用.文献[1-3]中的算法都必须有码速率和码同步的先验知识.Mounir Ghogho，Ananthmm和Tariq Durran给出一种简单的非线性频率估计方法[4](MAT算法)，MAT算法是一种简单快速实用的MPSK载频盲估计算法，但是如果输入的信号没有经过匹配接收或者匹配滤波，而接收机带宽远大于信号带宽，那么M次方这一非线性运算就会把大量的带外噪声叠加到有用信号的频带中，从而导致其估计性能下降.

在电子侦察领域，对接收的MPSK信号的参数没有任何先验知识，因此不能利用文献[1-3]中的算法估计信号的载频，而MAT算法的估计性能也受到限制.针对这一问题，文献[5]中提出了一种基于相位展开和最小二乘多项式拟合的算法(LSFE算法)，LSFE算法对MPSK信号参数的先验知识没有要求，且在较低信噪比(SNR)条件下载频估计的均方根误差(RMSE)依然接近MPSK信号的克拉美-罗限(MCRB).但是该算法的复杂度较高，因此处理时间也相应的比较长.由于电子侦察接收机对接收的信号没有任何先验知识，接收机带宽往往远大于接收到信号的带宽，并且由于是宽带接收，对其处理算法的实时性有很高的要求.针对这些特点，以计算量较小的MAT算法为基础，提出一种改进的MAT算法(本算法简称M-MAT算法)，使之可以应用到电子侦察等对信号参数没有任何先验知识的领域.首先在信号的频谱上估计出3 dB带宽，利用重心法粗略估计出接收信号的载频，然后以载频粗估计值为中心，以4倍3 dB带宽为带宽，对信号做带通滤波以滤除信号的带外噪声，再用MAT算法估计出信号的载频.分析表明这样处理可以有效地提高载频估计精度.本文中给出了M-MAT算法的适用条件.仿真结果表明，用M-MAT算法估计BPSK信号的载频，其估计精度在高信噪比条件下接近MPSK信号的克拉美-罗限(MCRB)，在低信噪比条件下明显优于MAT算法和LSFE算法，且本文中算法简单易行，仅在MAT算法的基础上增加了少量的处理，处理信号的实时性较好.

1 信号模型

有限观测时间内，复BPSK信号模型为：

(1)

其中A是信号幅度，fc是载频，φ0是初始相位，Nc是码元个数，T是观测时间，Tc是码元持续时间，C(m)是第m个码元，取值为0或1，∏是门函数，它定义为：

(2)

那么叠加了噪声的信号采样序列如下

(3)

Δt是采样间隔，v(n)是复零均值限带高斯白噪声，它的方差为σ2，通带为从0到1/Δt.N是样本个数.定义信号的信噪比(即输入信噪比)为： SNRI=A2/σ2

(4)

由(3)式可以得出，s(n)的主瓣宽度为： Bw=2/Tc

(5)

以fc为中心，c·Bw为带宽(c为正实数)，对x(n)作带通滤波，滤波后的序列xf(n)可表示为

xf(n)=sf(n)+vf(n)

(6)

sf(n)和vf(n)是以中心为fc，带宽为c·Bw(即2c/Tc)，分别对BPSK信号序列s(n)和噪声序列v(n)作带通滤波后得到的新序列.对xf(n)作平方运算得：xf2(n)=sf2(n)+vf2(n)+2sf(n)vf(n)

(7)

sf2(n)为信号项，vf2(n)+2sf(n)vf(n)为噪声项.xf2(n)在2fc处的能量谱密度为

EX(f)=ES(f)+EV(f)+ESV(f)

(8)

其中EX(f)、ES(f)、EV(f)和ESV(f)分别为xf2(n)、sf2(n)、vf2(n) 和2sf(n)vf(n)的能量谱密度.定义输出信噪比为： SNRo=ES(2fc)/[EV(2fc)+ESV(2fc)]

(9)

SNRo是在2fc处信号与噪声能量谱密度的比值.

2 ES(2fc)、EV(2fc)和ESV(2fc)的值

2.1 ES(2fc)的值 s(n)的频谱为：

(10)

那么sf(n)的频谱为：

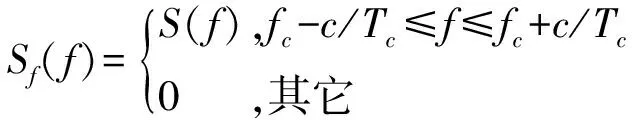
(11)

(12)

(13)

(14)

这是在2fc处信号能量谱密度归一化表达式，当c→∞时，R(c)→1.图1表示R(c)随c变化的曲线，可看出，若滤波带宽大于2倍信号带宽，2fc处sf2(n)的能量谱密度大于s2(n)的90%，而当滤波带宽小于2倍信号带宽时，R(c)值减小得很快，因此取c大于2较为合适.

图1 R(c)随c变化的曲线

2.2 EV(2fc)的值 复零均值限带高斯白噪声序列v(n)的功率谱为：

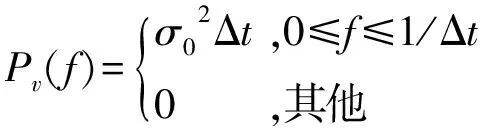
(15)

经过理想滤波后的噪声序列vf(n) 仍然是一个复零均值带限高斯白噪声，其功率谱为:

(16)

vf(t)的自相关函数为:Rvf(τ)=IFT{Pvf(f)}

(17)

其中IFT{x}表示x的逆傅里叶变换.

vf(t)是零均值复随机信号，因此E{vf2(t)}=0，则vf2(t)的自相关函数为:

(18)

因此vf2(t)的功率谱为：

(19)

那么在2fc处vf2(t)的能量谱密度为：

(20)

2.3 ESV(2fc)的值

2sf(t)vf(t)的自相关函数为:

R2sfvf(τ)=4Rsf(τ)·Rvf(τ)

(21)

因此2sf(t)vf(t)的功率谱为:

PSV(f)=FT{R2sfvf(τ)}=FT{4Rsf(τ)·Rvf(τ)}=4Psf(f)*Pvf(f)

(22)

Psf(f)是滤波后的接收信号序列sf(n)的功率谱，有

(23)

那么,2fc处2sf(t)vf(t)的能量谱密度为

(24)

3 SNRo(2fc)的分析

根据上节的分析，已经得到了ES(2fc)、EV(2fc)和ESV(2fc)的值，那么SNRo的值为:

(25)

图2 不同σ02值FSNRo随c变化的曲线

4 门限分析

基于DFT的频率估计算法的前提是xf2(n)的输出信噪比满足SNRo>25(约为14 dB)[7-8]，即

(26～27)

根据应用的不同，该式可以推出两个表达式.如果SNR已知，那么接收信号的点数必须满足:

N>100/[p(c)SNR]+50c/[p2(c)SNR2Mc]

(28)

如果接收信号的点数是固定的，那么SNR必须满足:

(29)

5 算法描述

根据前面的分析，现给出无任何先验条件下BPSK信号快速载频估计算法：

(1)对接收的BPSK信号序列做FFT，并对频谱做平滑；

6 仿真结果

用计算机仿真来考察本文中提出算法的性能.取BPSK信号为13位Barker码，采样频率fs=100 MHz，码宽为Ts=0.4 μs，载频为fc=0.421 3fs，在不同信噪比条件下分别用MAT算法、LSFE算法和本文中提出的M-MAT算法估计信号载频，其中M-MAT算法中取c=2，并统计出载频估计值的均方根误差，蒙特卡罗仿真次数为1 000次，仿真结果如图3所示.其中MPSK信号载频估计的均方根误差的克拉美-罗限[11-12]为：

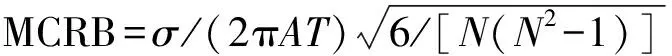
(30)

图3 BPSK信号载频估计的均方根误差

根据仿真条件可知，式(30)中各参数取值依次为N=40，Nc=13，c=2.由图1可知，当c=2时，R(c)的取值在0.90和0.92之间，那么p(c)的取值应该在0.95和0.96之间.因此，信噪比门限取值在4.64 dB和4.68 dB之间.从图3的仿真结果可以看出，用M-MAT算法估计BPSK信号的载频，其估计精度在高信噪比条件下接近MPSK信号的克拉美-罗限(MCRB)，在低信噪比条件下明显优于MAT算法和LSFE算法.当信噪比较低时，MAT算法和LSFE算法的性能较差，只有在信噪比较高的条件下，才能较精确的估计BPSK信号的载频.

7 结论

提出一种适用于二相编码信号载波频率估计的改进MAT算法，首先粗略估计出二相编码信号的载频及其带宽，然后对信号进行带通滤波，最后利用MAT算法得到BPSK信号的载波频率估计值.本算法仅在MAT算法的基础上增加了少量的处理，具有计算量小、实时性较好等特点，可以在低信噪比条件下实现BPSK信号的载频估计，具有一定的应用价值.

[1] Veterbi A J，Veterbi A M. Nonlinear estimation of PSK-modulated carrier phase with application to burst digital transmissions[J].IEEE Transactions on Information Theory，1983，IT-29:543-551.

[2] Mazzenga F，Corazza G E. Blind least-squares estimation of carrier phase，doppler shift，and doppler rate for M-PSK burst transmission[J].IEEE Communications Letters，1998，2(3):73-75.

[3] 李晶，朱江，张尔扬，等.高速8PSK调制信号的频率捕获及跟踪算法研究[J].信号处理，2005，21(1):66-69.

[4] Ghogho M，Swami A，Durrani T.Blind estimation of frequency offset in the presence of unknown multipath[A].IEEE International Conference on Personal Wireless Communications[C].Piscataway，NJ，2000:104-108.

[5] 邓振淼，刘渝.MPSK信号载频盲估计[J].通信学报，2007，28(2):94-100.

[6] 胥嘉佳，刘渝，邓振淼.任意点正弦波信号频率估计的快速算法[J].南京航空航天大学学报，2008，40(6):794-798.

[7] Rife D C，Boorstyn R R. Singla tone parameter estimation from discrete-time observations[J].IEEE Transactions on Information Theory，1974，IT-20:591-588.

[8] Shimon Peleg，Boaz Porat. Linear FM signal parameter estimation from discrete-time observations[J].IEEE Transactions on Aerospace and Electronic Systems，1991，27(4):607-616.

[9] Pinto E L，Brandao J C. A comparison of four methods for estimating the power spectrum of PSK signals[A].IEEE International Conference on Communications '87:Communications-Sound to Light[C].New York，1987:1749-1753.

[10] 邓振淼，刘渝.正弦波频率估计的牛顿迭代方法初始值研究[J].电子学报，2007，35(1):104-107.

[11] Dandrea A N，Mengali U，Reggiannini R. The modified cramer-rao bound and its application to synchronization problems[J].IEEE Transactions on Communications，1994，42(2-4):1391-1399.

[12] Gini F，Reggiannini R，Mengali U. The modified cramer-rao bound in vector parameter estimation[J].IEEE Transactions on Communications，1998，46(1):52-60.

[13] 潘志，贺祖琪.数学手册[M].北京：中国矿业大学出版社，1995.