地方税收收入预测的数学模型——以贵州省为例

余杨，王时绘

(湖北大学数学与计算机科学学院，湖北 武汉 430062)

0 引言

“地方税收收入”是指地方税务局系统负责征收的税收收入.地方税务局系统包括省、自治区、直辖市地方税务局，地区、地级市、自治州、盟地方税务局，县、县级市、旗地方税务局，征收分局、税务所.地方税收收入涉及的主要税种有营业税、城市维护建设税，地方国有企业、集体企业、私营企业缴纳的所得税、个人所得税、资源税、城镇土地使用税、耕地占用税、土地增值税、城市房地产税、车船使用税、车船使用牌照税、契税、屠宰税、筵席税等.

本文中主要研究地方税收收入预测的数学模型.

预测地方税收收入的数学模型国内外已经有很多学者进行研究.税收收入特别是地方税收收入有着与国外税收不同的规律，因此建立地方税收收入预测的数学模型既要考虑税收收入的变化规律，也要考虑地方税收收入的地域特点和地方经济发展规律.

郭菊娥等[1]运用因果模型对我国税收收入的影响因素进行验证，在其基础上构建税收收入的预测模型.徐利君等[2]在实证分析的基础上，得出地方税收收入与区域经济增长回归模型，探讨不同区域地方税收收入对经济发展水平的影响.曾纪芬[3]运用统计、对比分析方法，探索地方经济与税源以及税收三者之间的关系.广州市地方税务局课题组[4]以1999-2005年为分析期，对“十一五”期间六城市地方税收的增长趋势进行预测.刘明珠等[5]分析了利用SPSS进行税收预测要注意的问题.李扬[6]研究了相关联的若干经济指标与国税收入之间的相互依赖、相互制约的影响程度.贵州省地方税务局课题组[7]分析了1996-1999年贵州省地方税源结构，并对2000年地方税收年增长率进行预测.王碧秀[8]研究了地税收入总量与经济总量的关系；地方税收与地方产业结构的关系；地方税收与税种及地方经济的关系.李洁[9]和张鑫[10]研究了采用组合预测方法对省级税收收入进行预测，并用历史数据对模型进行实证检验.

1 数据和模型

本文中使用的数据包括1999-2009年贵州省地方税收收入、贵州省GDP、贵州省居民消费价格指数CPI和工业品出厂价格指数PPI.所有数据主要来源于1999-2009年各年《贵州统计年鉴》(中国统计出版社)和国家统计局网站.

我们建立的贵州省地税税收收入预测模型主要是曲线估计模型、线性回归模型和时间序列模型.考虑到以地方税收收入为单一变量的时间序列模型本身难以反映和解释经济增长对税收收入的影响，因此在建立税收收入时间序列预测模型时，建立了税收收入的计量经济学预测模型.具体建模时主要考虑地方宏观经济量与地方税收收入之间的相互关系，采用年度数据建立以地方税收收入为因变量，地方宏观经济变量为自变量的整合自回归移动平均(autoregressive integrated moving average，ARIMA)预测模型，对地方税收收入进行预测.

在建立贵州省地方税收收入预测模型时，我们还建立了地方税收收入的曲线估计模型.根据地方税收收入在较长一段时间的发展趋势以及地方税收收入随时间变化的数量关系(这种关系不是一种因果关系，而是一种结构关系[11])，建立了地方税收收入的曲线估计模型(趋势外推模型).

1.1模型1：税收收入总量的趋势外推模型——Cubic模型很多变量的发展变化与时间之间都存在一定的规律性，趋势外推预测法是研究变量的发展变化与时间之间的函数关系.根据函数关系的形态不同，可分为直线趋势外推预测法、曲线趋势外推预测法.

曲线外推预测法是指根据时间序列历史数据的散点图的曲线变化趋势，选择恰当的曲线方程，利用最小二乘法确定待定的参数，建立曲线预测模型，并用它进行预测的方法.

常见的曲线外推趋势预测法有二次曲线法、三次曲线(Cubic)法等.

本文中将1999-2009年贵州省地方税收收入数据作为时间序列，并对其进行各种曲线拟合，结果发现所有曲线趋势中以三次曲线(Cubic)法的各项统计结果最为理想，因此，建立贵州省地方税收收入的趋势外推模型——Cubic预测模型[11].

(1)

1.2模型2:税收收入总量TAX与国内生产总值GDP的回归模型参考税收理论与税收预测研究[1，9-10]，宏观经济量中对税收收入影响最大的是国内生产总值GDP[2，8，12].为此，本文中利用SPSS统计软件，选取 1999-2009年贵州省地方税收收入TAX和贵州省国内生产总值GDP数据进行相关分析.

相关分析的结果表明:ln(GDP)与ln(TAX)的相关系数为 0.99；ln(GDP)与ln(TAX)的校正R2值为 0.997，说明GDP是影响地方税收收入的主要因素.

地方税收收入TAX与国内生产总值GDP的回归模型方程为：ln(TAX)=aln(GDP)+b

(2)

式中：ln(TAX)为第t期地方税收收入TAX的对数(因变量)；ln(GDP)为第t-1期国内生产总值GDP的对数(自变量)，t=1，2，…，n.

1.3模型3:地方税收收入与地方宏观经济指标的ARIMA模型ARIMA模型是1970年Box和Jenkins提出的时间序列模型.ARIMA模型在应用中需要通过若干次差分将非平稳时间序列转化为平稳时间序列，再对此平稳时间序列进行定阶和参数估计，从而对时间序列进行预测分析.

为了进一步考察宏观经济量对地方税收收入的影响，利用SPSS统计软件，选取1999-2009年国内生产总值GDP、全社会固定资产投资TI、社会消费品零售总额 TR、居民消费价格指数CPI、财政支出CZZC以及工业品出厂价格指数PPI等经济变量，考察地方税收总收入与各宏观经济变量间的相关关系.

从相关关系分析的结果可以获得以下结论:众多宏观经济量中，国内生产总值指数(取ln(GDP))，居民消费价格指数(取ln(CPI))，工业品出厂价格指数(取ln(PPI))与地方税收收入指数(取ln(TAX))的相关系数较高，分别为0.998 6，0.830 3和0.727 1；说明国内生产总值，居民消费价格指数和工业品出厂价格指数是影响地税总收入的主要宏观经济量.进一步，我们建立以上宏观经济量与地方税收收入之间的多个ARIMA模型，经过不断比较和调整系数，最后在众多模型中选择了拟合效果好而且误差较小的ARIMA(1，0，0)模型[5-6，11-12].

利用SPSS统计软件，选取1999-2009年贵州省地方税收收入指数(取ln(TAX))为因变量，国内生产总值指数(取ln(GDP))，居民消费价格指数(取ln(CPI))和工业品出厂价格指数(取ln(PPI))为自变量，建立税收收入TAX与GDP和CPI以及PPI的ARIMA(1，0，0)模型方程为：

Wt=φ1Wt-1+et,t=1，2，…，n

(3)

其中Yt{y1，y2，y3…}是第t期变量的值，通过对数变换成平稳时间序列Wt，对于平稳时间序列Wt，Wt满足ARMA(1，0)模型.

2 模型参数估计和检验

将1999-2009年贵州省地方税收收入、国内生产总值GDP和贵州省居民消费价格指数CPI和工业品出厂价格指数PPI等数据分别代入上述3个模型，利用SPSS软件计算，结果见表1、表2和表3.

表1 模型1：Cubic模型参数估计

校正R2为0.999，F=3 758.668，p值Sig.=0.000<0.05

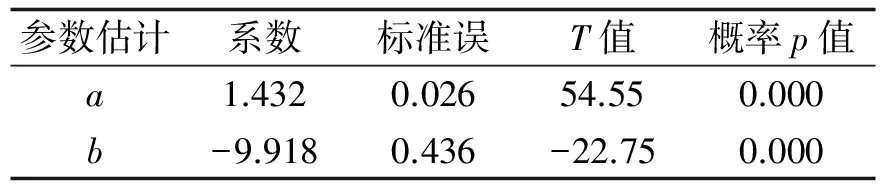
表2 模型2：税收收入总量与GDP总量的回归模型参数估计

校正R2为0.997，F=2 975.44，p值Sig.=1.42E-11<0.05

表3 模型3: 税收收入总量与GDP总量、居民消费价格指数和工业品出厂价格指数的 ARIMA(1，1，0)模型参数估计

校正R2为1.000，MAPE=0.741

3 模型拟合值和误差

表1至表3的结果说明，3个模型的拟合度较高，统计检验显著，说明模型提供的信息是可信的，可以用来预测税收收入.利用这些模型对贵州省2009年地方税收进行具体测算，得出各个模型2009年贵州省地方税收收入预测值及相对误差结果如表4.

表4 各个模型拟合结果及相对误差 万元，%

4 地方税收收入的组合预测模型

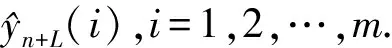
(4)

minQ=WTEWs.t.RTW=1.

由拉格朗日乘数法得权重系数向量:

W=(RTE-1R)-1E-1R

(5)

4.2地方税收收入的组合预测模型结果由前面的3种单一模型可以得出2000-2009年地方税收收入的拟合值，实际地方税收收入与拟合值的差就是预测误差，由此可得出一个误差表，然后可以在EXCEL中计算3个模型的权重.

本文中由公式(5)计算得到的权重系数结果为：w1=1.214，w2=-1.123，w3=0.909，

其中w1是模型1的权重，w2是模型2的权重，w3是模型3的权重.

结果表明最优加权系数中存在着负数，得到的最优组合预测模型失效.

通过计算可以得到最优加权系数为：

k1=0.890 2，k2=0.109 8,

其中0.890 2为模型1在进行组合预测时的加权系数，0.109 8为模型3在进行组合预测时的系数.

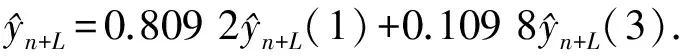
为了检验组合预测的预测效果，对历史数据进行拟合，得到结果见表4.

5 模型评价

对模型1，模型2，模型3根据预测的目的构造损失函数，使损失函数取得最小值的就是最优的预测模型.本文中利用MSE(均方误差)准则，即如将若干不同的预测方法用于同一预测对象，则MSE最小的模型最优.均方误差MSE公式为：

利用MSE准则对每种预测方法进行评价，所得结果见表4.

从表4中可以看出组合预测模型的MSE最小，所以利用组合预测模型对未来地方税收收入的预测所得的效果要优于其他的单一预测模型.

6 结论

本文中建立地方税收收入的3种单一预测模型，并在这3种模型的基础上构建基于均方误差MSE最小的地方税收收入的组合预测模型.由于单一模型假设存在一些不确定性，因此单一模型的预测结果也难免存在一些不确定性，如经济危机、国内重大自然灾害、物价指数以及宏观经济量之间关系的变动.不过只要以上单一模型假设发生变化，我们可以对模型中的变量进行调整，使模型适应国际经济环境、国内经济形势的变化、政府出台的宏观经济政策和一些改革措施.并且在3种单一模型的基础之上，构建了基于Cubic趋势外推模型、税收收入总量TAX与GDP总量回归模型以及税收收入总量与GDP总量、居民消费价格指数和工业品出厂价格指数的ARIMA(1，0，0)模型的组合预测模型用于地方税收收入预测，利用贵州省地方税收收入数据进行的实证研究表明：利用组合模型进行地方税收收入预测，具有均方误差MSE较小的优势，进一步可以探讨进入组合模型中单一模型的选择和不同单一模型进行组合的方式等研究，从而建立更准确的地方税收收入预测模型.

致谢：论文写作过程中，湖北大学软件研究所的各位老师在数据收集等方面给予了无私的帮助，贵州省地方税务局杨军副局长和贵州省地方税务局信息处刘长勇主任以及贵州省地方税务局征管和科技发展处罗玉平处长对论文提出了宝贵的意见，六盘水市地方税务局江华总经济师也对论文提出了宝贵的建议和意见，在此一并表示感谢.

[1] 郭菊娥，钱鑫，曹华.2004 年中国税收收入预测研究[J].财经科学，2003(增刊): 392-394.

[2] 徐利君，徐冯璐.地方税收收入与区域经济发展的实证分析[J].科技和产业，2008，8(2):66-69.

[3] 曾纪芬.培育地方税源研究——以广西为例[J].经济研究参考，2010(17):26-35.

[4] 广州市地方税务局课题组.广州、北京等六城市地方税收增长态势比较研究[J].税务研究，2007(2):58-64.

[5] 刘明珠，赵晓萍，傅志华.灵活运用SPSS进行税收预测[J].中国发展，2005(4):38-42.

[6] 李扬.新疆国税系统建立税源分析预测数学模型初探[J]，新疆财会，2008(2):56-61.

[7] 贵州省地方税务局课题组.贵州省税源分析与预测[J].经济研究参考，2000，118:42-48.

[8] 王碧秀.地方税收与地方经济的关系研究[J].山东社会科学，2009(10):101-104.

[9] 李洁.四川省税收收入预测模型探讨及实证分析[D]．成都：西南财经大学，2004:55-59.

[10] 张鑫.基于组合模型的黑龙江省税收收入预测研究[D]．哈尔滨：哈尔滨工业大学，2009:33-37.

[11] 薛微.SPSS统计分析方法及应用[M].北京：电子工业出版社，2004.

[12] 计量经济模型与经济预测[M].4版，钱小军，译.北京：机械工业出版社，1991.