具有S分布时滞细胞神经网络的全局指数稳定性＊

谌红美，王林山

（中国海洋大学数学科学学院，山东青岛266100）

具有S分布时滞细胞神经网络的全局指数稳定性＊

谌红美，王林山

（中国海洋大学数学科学学院，山东青岛266100）

研究了一类具有S分布时滞细胞神经网络的全局指数稳定性。利用Banach不动点定理，通过构造Lyapunov泛函，结合Hardy不等式和推广的Halanay时滞微分不等式，给出了全局指数稳定性的充分条件，并做出了比较说明。

细胞神经网络；S分布时滞；Lyapunov泛函；全局指数稳定性

近年来，时滞细胞神经网络受到广泛关注，研究成果不断涌现［1－6］。由于具有S分布时滞的系统既包含了离散时滞系统又包含了分布时滞的系统［1，7］，因此，对具有S分布时滞细胞神经网络的研究更有理论和实际意义。本文研究了具有S分布时滞细胞神经网络的全局指数稳定性，并去掉了文献［8］中激活函数有界性条件，同时为了避免出现爆破现象，研究了解的有界性。

1 预备知识

考虑如下具有S分布时滞细胞神经网络模型

其中n是神经元的个数，xi（t）表示第i个神经元在时刻t的状态变量，fj（xj（t））表示第j个神经元在时刻t的输出，aij和bij表示神经元之间的连接权重，Ii是对第i个神经元的偏置，ci＞0表示在与神经网络不连通并且无外部附加电压差的情况下第i个神经元恢复孤立静息状态的速率。是不减的有界变差函数关于在上的Lebesgue－Stieltjes积分，且满足条件是有界连续函数。

假设（H）：存在常数ui＞0，使得

引理1［9］（Hardy不等式）假设a和b是非负实数，

则

当且仅当a＝b时等号成立。

引理2［1］（推广的Halanay时滞微分不等式）设常数，函数V（t）是的非负连续函数，且时，则有，其中κ是超越方程的唯一正根为常数。

2 主要结果

λ≥1，则系统（1）有唯一的、全局指数稳定的平衡点。证明 （a）平衡点的存在唯一性

即

由（2）式可知，当λ＝1时，若核函数值｜ki｜≤1，则有

令

则存在常数η1，满足；若核函数值取，则有

令

则存在常数η2，满足。取且令

则Q是Rn中的一个有界闭凸子集。对于y∈Q，当时，有

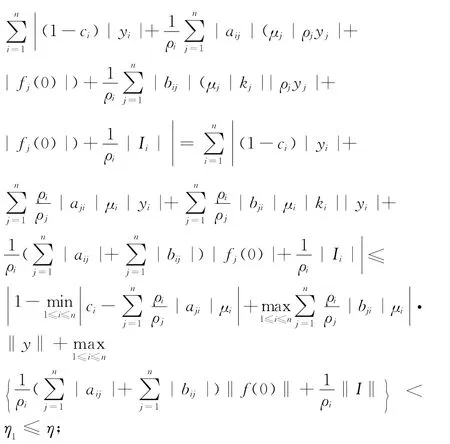
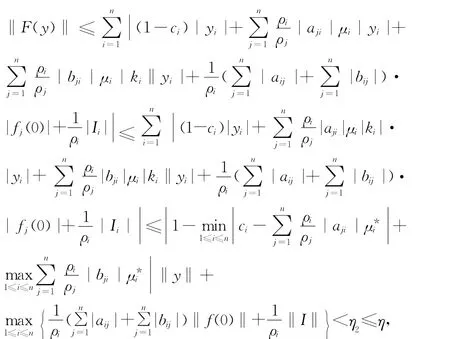
从而F（y）∈Q，即F是Q上的自映射。

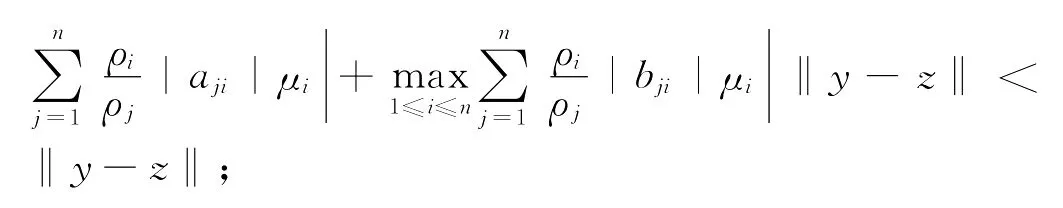
当｜ki｜＞1时，由（6）式可知

综上所述，F是Q上的压缩映射，由Banach不动点定理知，F在Q内有唯一不动点y＊，由（3）和（4）的等价性知，系统（1）有唯一平衡点。

（b）系统（1）的解的有界性

为避免系统（1）的解在有限时间内产生爆破现象，下证（1）的解是有界的。

设x（t）是异于x＊的任意解。令，则

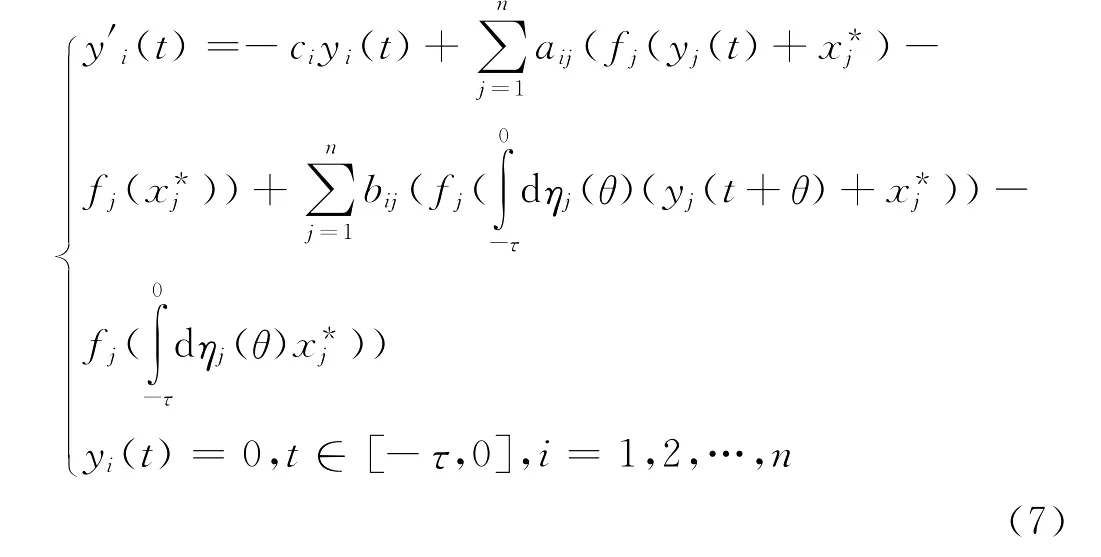
显然，系统（1）解的有界性等价于系统（7）解的有界性。假若系统（7）解的无界，则至少存在一个解y（t）和t1＞0，使得，且由ci＞0，（7）式和常数变易公式得

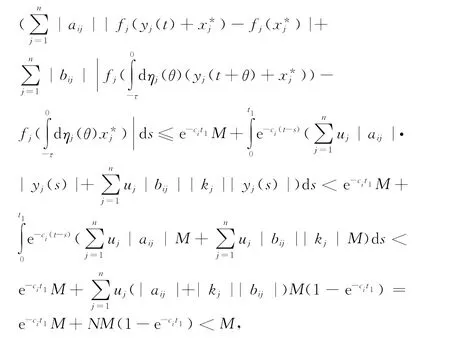
（c）平衡点的全局指数稳定性

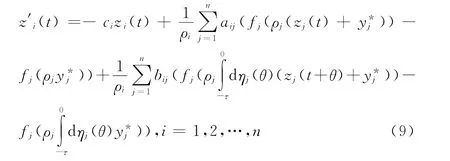
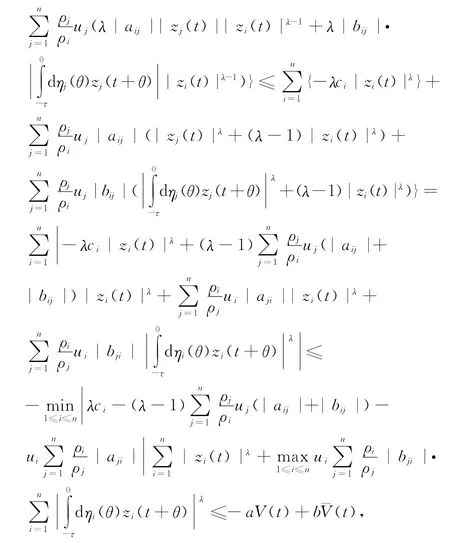
其中

其中κ是超越方程κ＝a－beκτ的唯一正根。从而由（10）知，系统（1）的平衡点全局指数收敛。

3 比较说明

考虑如下2种神经网络模型：

离散时滞与分布时滞2种类型的细胞神经网络模型是互不包含的，然而S分布时滞的细胞神经网络模型却包含了这2种类型的细胞神经网络模型。如上述模型，ηj（θ）是（－∞，0］上的不减有界变差函数，当取

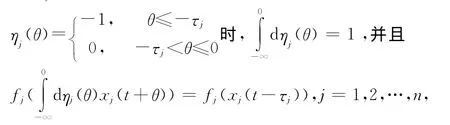
即模型Ⅱ，这是文献［8］中所研究的结果；当ηj（θ）连续可微且η′j（θ）＝kj（－θ），j＝1，2，…，n时，则

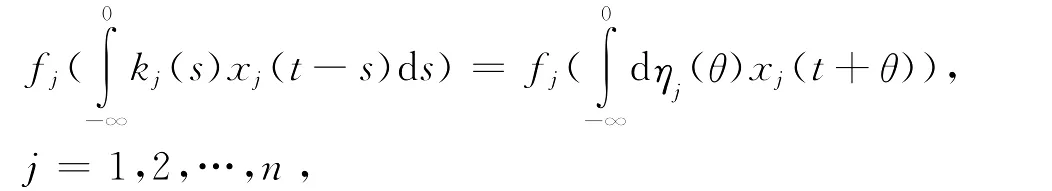
即连续型的细胞神经网络模型，这是文献［10］中所研究的结果，从而S分布时滞的细胞神经网络模型既包含了离散型的系统又包含了连续型的系统。

4 结语

本文利用Banach不动点定理，通过构造Lyapunov泛函，结合Hardy不等式和推广的Halanay时滞微分不等式，研究了一类具有S分布时滞细胞神经网络的全局指数稳定性，给出了全局指数稳定性的充分条件。去掉了文献［8］中激活函数有界性条件，同时为了避免出现爆破现象，研究了解的有界性，最后通过比较说明了S分布时滞的细胞神经网络模型包含了离散型和连续型这2种类型的细胞神经网络模型。

［1］ 王林山.时滞递归神经网络［M］.北京：科学出版社，2008.

［2］ 廖晓昕.细胞神经网络的数学理论（Ⅱ）［J］.中国科学（A辑），1994，24（10）：1037－1046.

［3］ 廖晓昕.细胞神经网络的定性研究［J］.华中师范大学学报，1994，28（6）：141－145.

［4］ 张若军，王林山.S分布时滞区间细胞神经网络的全局渐近鲁棒稳定性［J］.山东大学学报：理学版，2007，42（2）：39－42.

［5］ 刘炳文.时滞细胞神经网络的周期解、概周期解和全局指数稳定性［D］.长沙：湖南大学，2005.

［6］ Zhou D M，Cao J D.Global expontial stability conditions for celler neural networks with time－varying delay［J］.Appl Math Comput，2002，131：487－496.

［7］ 郑祖庥.泛函微分方程［M］.合肥：安徽教育出版社，1994.

［8］ 李拥军，吴洪武.具变时延细胞神经网络模型的全局指数稳定性［J］.系统工程，2006，24（8）：119－122.

［9］ Hardy G H.不等式［M］.越民义，译.北京：人民邮电出版社，2008.

［10］ 戴志娟.具有连续分布延时的细胞神经网络的全局指数稳定性［J］.扬州职业大学学报，2010，14（2）：30－34.

Global Exponential Stability of Cellular Neural Networks with S－Distributed Delays

CHEN Hong－Mei，WANG Lin－Shan
（School of Mathematical Science，Ocean University of China，Qingdao 266100，China）

Global exponential stability of cellular neural networks with S－distributed delays is considered.A sufficient condition to guarantee the global exponential stability is obtained by using Banach＇s fixed point theorem，constructing Lyapunov＇s functional and combining with Hardy inequality and the promotion of the Halanay＇s delay differential inequality.And made comparison to illustrate the result.

neural networks；S－distributed delays；Lyapunov function；global exponential stability

O175

A

1672－5174（2012）03－096－05

国家自然科学基金项目（11171374）；山东省自然科学基金重点项目（ZR2011AZ001）资助

2011－05－03；

2011－09－05

谌红美（1985－），女，硕士生，研究方向：动力系统与人工神经网络。E－mail：shmcyy＠sina.com

AMS Subject Classification:39A11

责任编辑 朱宝象