圆环区域上带梯度项的椭圆型方程径向大解的爆破速率＊

方钟波，茹海霞

（中国海洋大学数学科学学院，山东青岛266100）

圆环区域上带梯度项的椭圆型方程径向大解的爆破速率＊

方钟波，茹海霞

（中国海洋大学数学科学学院，山东青岛266100）

本文研究在圆环区域上带梯度项和完全非线性项的半线性椭圆型方程边值问题径向大解的爆破速率。在证明一些重要极限的基础上，与常微分方程分析法相结合得到了当完全非线性项满足Keller－Osserman条件，梯度项的指数范围分别在0～1和大于2时径向大解的爆破速率及在加强的条件下大解边界行为的第二次影响.

椭圆型方程；大解；爆破速率

0 引言

本文考虑圆环区域上具有梯度项和完全非线性项的半线性椭圆型方程

当方程不带梯度项时，早在1916年，L Bieberbach［1］在有界区域上研究了具有指数型非线性项的半线性椭圆型边值问题大解的存在唯一性和边界行为。之后，有关代数型非线性项［2］的半线性椭圆型边值问题大解的研究得到了较快发展且已有丰硕的成果［3－7］。最近，Bandle等在考虑圆环区域中具有完全非线性项的半线性椭圆型边值问题时也得到了径向大解的存在唯一性及其边界爆破速率［8－10］。

当方程带梯度项时，有关指数型、代数型、完全非线性项的半线性椭圆型边值问题在适当条件下大解的存在性结论较完善［11－13］。特别地，文献［12］利用上下解的方法研究了当f（u）为满足Keller－Osserman条件的源项及梯度项的指数p满足1＜p＜2时大解的存在性及渐近行为。据文献所知，当Ω为圆环区域且非线性梯度项的指数p满足0＜p≤1或p＞2时，其边值问题径向大解渐近行为的研究还未得到展开。

本文主要研究在圆环区域中，当f（u）满足Keller－Osserman条件且非线性梯度项的指数范围为0＜p≤1或p＞2时，方程（1）径向大解的爆破速率以及0＜p≤1范围内边界行为的第二次影响。具体结论如下：定理1 设0＜p≤1或p＞2且条件（f1），（f2）成立，则下面结论成立。

1）若v（r）是方程（1）在Ω＝｛x｜ρ＜｜x｜＜R｝内的一个径向解，且满足那么有

2）若w（r）是方程（1）在Ω＝｛x｜ρ＜｜x｜＜R｝内的一个径向解，且满足，那么有

记

则由定理1可知

如果定理1的条件再加强一些，并且当非线性梯度项的指数范围为0＜p≤1时，利用（4）～（6）的估计式即可得到边界行为的第二次影响。

定理2 设v（r），w（r）是方程（1）在Ω内的解（定义同定理1），f满足（f1），（f2），（f3）那么当0＜p≤1时，下面结论成立。

1）设δ＝R－r，记o（1）是δ→0时趋向于零的一个量，则存在常数c1，使得

2）设δ＝r－ρ，记o（1）是δ→0时趋向于0的一个量，若成立，则存在常数c2，c3，使得

注2 在定理2考虑边界行为的第二次影响时，按照现有的方法，将无法得到当p＞2时的上界估计值，故仅考虑了0＜p≤1的情形。

1 预备知识

本节先介绍2个引理及命题，在后面证明主要结论的过程中起到了关键的作用。

引理1 设f（t）满足（f1），（f2），则当0＜p≤1或p＞2时，有

证明 利用反证法。

假设

由（f2）知，ψ（t）存在，且。故存在1个递增序列tk→∞（k→∞），使得当β＝μ＋1时，F（tk）＝

另一方面，由（f1）可知，当t＞t0时F″（t）＞0且F（t）是凸函数，则当t∈［tk，tk＋1］时，

进而得

及

由（9）、（10）、（11）式及ψ（t）存在可知，当0＜p≤1或p＞2时，有

导致矛盾。

由（f1）条件知，对t＞t0，有

故利用引理1和（12）式，直接得到下面的引理。

引理2 若f满足（f1），（f2），则当0＜p≤1或p＞2时，有

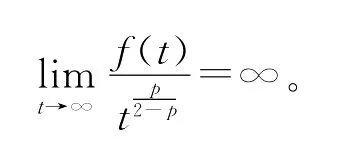
命题1 若f满足（f1），（f2），则当0＜p≤1或p＞2时，有

证明 由引理1知

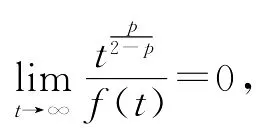
且当t→∞时有

由于F（t0）＝0，故

考虑圆环区域Ω＝｛x｜ρ＜｜x｜＜R｝内的径向对称解。为了方便起见，记

则由命题1和洛必达法则易知

2 主要结论的证明

定理1的证明 若v（r）是方程（1）在Ω＝｛x｜ρ＜｜x｜＜R｝内的一个径向解，且满足，则当r∈（ρ，R）时，v（r）满足方程

（16）式两边同时乘以v′，且在（r0，r）上积分可得

其中：

当r充分接近R时，有v′（r）＞0。否则，由v（r）＝∞（r→R）知，在R的左邻域［r1，R）内存在一点r2∈［r1，R），满足v′（r2）＝0且v″（r2）＜0，代入（16）式即可得到v″（r2）＝f（v（r2））＜0，与f（v（r））＞0矛盾。

易知，可取珘r充分接近R，使得v在（珘r，R）上单调递增，且当r0∈［珘r，R］时，有

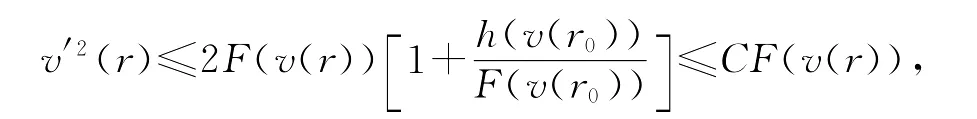
其中：C为常数。从而可得：

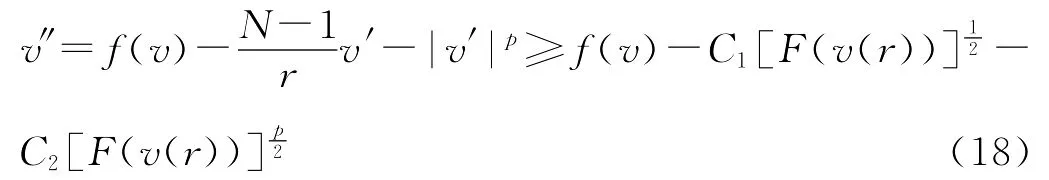
其中：C1，C2为常数。

由（18）及命题1可知，v′在R的左邻域内单调递增且有

其中当r0→R时，可取ε1，ε2任意小。

结合（19）（20）及（17）式可得

因此，当r0→R时，有

进而有

结合（22）、（23）及（17）式可得

因此，由（15）式可知

当r→R时，取极限即可得到（2）式。

类似地，可以得到（3）式。

定理2的证明 先证明结论1）。

由（13）、（14）及F（t）在（t0，∞）中的单调性知，当v（r）＞t0时，有

并且当r0充分接近R时，v（r）在（r0，R）上单调递增。故由（f3）及（24）式知

将这个不等式内插入（6）式的第一部分，利用（4）式和（25）式可得，当0＜p≤1时

下证右半部分。由（26）式可知

即

若（f4）成立，下证2）式成立。当δ→0时，珘ω→0，珘α→0，故有

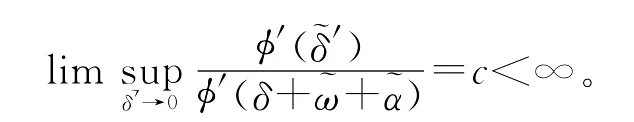
由（6）式的第二部分知

进一步，由（f3），（5）和（24）可得

因此，当0＜p≤1时，有

由（27），（28）和6）式的第二部分，即可得到（8）式。

［1］ Bieberbach L.Δu＝euund die automorphen Funktionen［J］.Math.Ann，1916，77：173－212.

［2］ Rademacher H.Einige becondere probleme paitieller differential－gleichungen［M］.∥Die differential－und－integragleichungen der Mechanik I，2nd edition.New York：Rosenberg，1943，838－845.

［3］ Cheng jiangang，Guang Luo.Uniqueness of positive radial solutions for Dirichlet problems on annular domains［J］.Math Anal－Ap，2008，338：416－426.

［4］ Coffman C V.Uniqueness of the positive radial solutions on an annulus of the Dirichlet problem forΔu－u＋u3＝0［J］.Differ Equat，1996，128：379－386.

［5］ Xabier Garaizar.Existence of positive radial solutions for semilinear elliptic equations in the annulus［J］.Differ equat，1987，70：69－92.

［6］ Chun Chieh Fu，Song Sun Lin.Uniqueness of positive radial solutions for semilinear elliptic equations on annular domains［J］.Nonlinear Anal，2001，44：749－758.

［7］ Juan Davila，Marcelo Montenegro.Radial solutions of an elliptic equation with singular nonlinearity［J］.Math Anal Appl，2009，352：360－379.

［8］ Bandle C，Marcus M.On second order effects in the boundary behaviour of large solutions of semilinear elliptic problems［J］.Differ Int Equat，1998，11：9－24.

［9］ 郝晓燕，程建纲.环形区域上Dirichlet问题正径向解的唯一性［J］.烟台大学学报，2009，22（2）：83－86.

［10］ 李永祥.球外部区域上非线性椭圆方程的正径向解［J］.数学研究与评论，2005，25：128–133.

［11］ Bandle C，Giarrusso E.Boundary blow up for semilinear elliptic equations with nonlinear gradient terms［J］.Adv in Differ Eq，1996，1：133－150.

［12］ Giarrusso E.Asymptotic behaviour of large solutions of an elliptic quasilinear equation in a borderline case［J］.Sci Paris Ser I Math，2000，331：777－782.

［13］ Saloman Alaroon，Jorge Garcia－Mellan，Alexander Quaas.Keller－Osserman type conditions for some elliptic problems with gradient terms［J］.J Differ Equations，2012，252：886－914.

The Blow－up Rates of Large Radial Solutions for the Elliptic Equation with Gradient Term in Annular

FANG Zhong－Bo，RU Hai－Xia
（School of Mathematical Science，Ocean University of China，Qingdao 266100，China）

In this paper，the blow－up rates of large radial solutions for the semilinear elliptic equation with gradient term and fully nonlinear term in annular domain was investigated.On the basis of the proof of some important limits，using ordinary differential equation analysis method，we achieved the blow－up rates of large radial solutions when fully nonlinear term satisfies the Keller－Osserman conditions and the exponential of gradient term ranges from 0 to 1 or larger than 2.Moreover，we considered a secondary effect on the asymptotic behavior of solutions under the enhanced conditions.

elliptic equations；large solution；blow－up rate

O175

A

1672－5174（2012）09－115－04

国家留学回国人员科研启动基金项目（910937020）资助

2011－05－29；

2011－09－01

方钟波（1968－），男，副教授，硕导。E－mail：fangzb7777＠hotmail.com

AMS Subject Classification:35J25，35J65

责任编辑 陈呈超