波浪对海洋上混合层温度变化的影响研究＊

张晓爽，吴克俭

（1.中国海洋大学海洋环境学院，山东青岛266100；2.国家海洋局海洋环境信息保障技术重点实验室国家海洋信息中心，天津300171；3.中国海洋大学物理海洋实验室，山东青岛266003）

波浪对海洋上混合层温度变化的影响研究＊

张晓爽1，2，吴克俭1，3＊＊

（1.中国海洋大学海洋环境学院，山东青岛266100；2.国家海洋局海洋环境信息保障技术重点实验室国家海洋信息中心，天津300171；3.中国海洋大学物理海洋实验室，山东青岛266003）

通过在海洋上混合层温度方程的平流输运项中加入Stokes漂的影响，定量计算了波浪Sokes漂对混合层温度变化的贡献，即Stokes漂对SST变化的影响。结果表明，波浪Stokes漂的平流输运作用对混合层温度变化的贡献与平均流的贡献在量值上处于可比的量级，二者全球平均比值为23.43%，最大比值达到70%。而对于SST变化率的影响也较为显著，加入Stokes漂影响后，SST变化率的最大变化值达到0.989×10－6℃／s，SST变化率的全球平均变化值为0.077 8×10－6℃／s，与SST变化率全球平均量值0.516 2×10－6℃／s相比达到15.07%，是不可忽略的。因此，在对于海洋混合层温度计算过程中，考虑波浪Stokes漂的作用是必要的。

Stokes漂；混合层；SST变化率；平流输运

近年来波浪对海洋大尺度物理过程的影响日益引起人们的关注，Qiao等［1－2］和杨永增等［3］研究了波浪对海洋垂向混合的贡献，发现波浪的混合作用对于上层海洋温跃层的形成具有重要的作用，并依据浪致混合的表达改进了大洋环流的湍混合模式；Li和Song等［4］研究了Stokes漂流对海洋上混合层的影响，结果指出在上层海洋的混合过程中，波浪Stokes漂提高了耗散率以及扰动能量，并且与海表面热量吸收，以及波浪破碎作用相比，Stokes漂在上层海洋的混合中起到更加重要的作用。上述研究工作主要针对波浪对海洋的垂向混合方面的作用。

波浪的Stokes输运在上层海洋的水平输运过程中同样起到不可忽视的作用。Longuet－Higgins［5－6］研究发现，在旋转海洋中，即使考虑很小的粘性效应，波浪诱导的水平输运也会改变海洋上层流动。Kenyon［7］将海表面Stokes漂流速度与风速建立相关，认为Stokes漂流速度是随着风速大小变化的，同时Stokes输运可能会对海表面总的平均流产生重大影响。Weiber［8］，Jenkins［9］分别在Lagrange坐标系下研究了风驱Ekman漂流和波浪驱动的Ekman漂流，得出相似结论，风驱Ekman漂流和波浪驱动的Ekman漂流具有相似量级。Mcwilliams［10］对波浪驱动大洋环流进行了研究，指出在较大的水平尺度上，海洋中存在表面重力波对Sverdrup输运具有重要贡献，并且在中高纬度地区波浪驱动的输运与风生环流输运达到同等的量级。Lane［11］将辐射应力和涡度力引入到流守恒方程中，从动力学上将波浪与流建立关系。Wu［12］进一步从能量角度阐述了波浪对大尺度海洋运动的驱动作用，指出在高纬度、高风速下，Ekman－stokes层波浪输入能量与总风能输入之比超过10%，在南极绕极流区域甚至可以达到22%。邓增安等［13］和张坤兰等［14］通过研究太平洋波浪输运，发现波浪诱导的输运对西边界流乃至整个环流都有重要影响。Deng［15］通过风－流耦合模型对海表面流速导致的风应力变化对海洋热通量，海表面温度的影响进行了研究。结果表明，耦合模型对海表面温度和热通量的模拟能力与非耦合流模式相比有显著提高，海表面温度平均改变2%，热通量平均改变10%。并指出海表面波浪诱导的速度对风应力的影响同样不可忽视，海表面波浪诱导速度引起的风应力平均变化率为5%，海表面平均流流速引起的风应力变化率为3.5%，二者共同作用下风应力的变化率达到8%。由此可知，海表面波浪对海表面温度，热通量，等上层海洋现象存在较为重要的影响。

由以上波浪大尺度效应的研究可知，波浪的大尺度物理过程，在上层海洋垂向混合与水平输运方面都具有不可忽视的重要作用。而且在水平输运方面，波浪不仅能够通过体积输运，能量输运对大洋环流系统造成影响，同样能够影响到上层海洋的温度变化等现象。但是迄今为止尚未见任何工作对波浪影响海洋混合层温度变化进行定量的研究，波浪对混合层温度的确切影响方式，及影响量值大小目前仍然属于未知。

本文旨在从波浪的水平输运角度，探讨波浪对海洋混合层温度变化的影响机制。通过在混合层温度变化方程的水平输运项中加入波浪的水平输运，定量计算波浪诱导的水平输运对海洋上混合层温度（即SST）变化的贡献值。并在此基础上分析浪致水平输运对于混合层温度变化的重要性。

1 理论依据与数据简介

1.1 混合层温度方程

Stevenson［16］指出，通过上层海洋的热量守恒方程和质量守恒方程获得的忽略水平热扩散的上层海洋热力学方程可以写为：

其中：T为海水温度；V为水平流速矢量；w为垂向流速；ρ为海水密度；Cp为海水比热；Q为垂向热通量；K为垂向热量扩散系数。

将方程1向下对z从海面积分到－h深度，即可得到－h深度以上海洋的温度变化方程：

方程2左边1项表示平均温度的变化；右边第1项为上层海洋净热通量的影响；右边第2项，第3项表示温度的平流输运的影响；右边第4项为垂直卷夹的影响。若h选取为混合层深度或者较浅深度，此方程可看做SST的变化方程。

目前温度平流变化项中流速的选取主要为上层海洋平均流流速，并没有考虑波浪Stokes漂流所导致的平流作用，而Stokes漂流对海表面平均流场具有重要的影响，Lane［11］对于波流相互作用的研究中指出，波浪示踪通量的散度等于由Stokes漂流流速所导致的平均波浪示踪的平流输运效应，即：

其中：c为示踪物；cw为波浪输运的示踪物为波浪对示踪物输运的速度；ust为波浪Stokes漂流流速。波浪Stokes漂流在示踪物输运方面与平均流起到同等作用，因此平均流与波浪共同作用所致的平流输运方程可表示为：

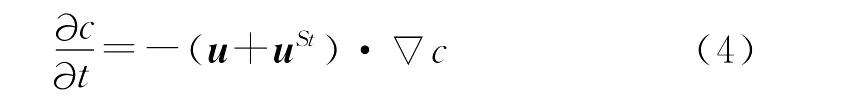
波浪Stokes漂流能够与平均流共同对示踪物的平流输运产生贡献，因此对于热力学方程（1）中温度的平流输运项，Stokes漂流的平流输运作用的贡献亦是必然存在的，因此在温度平流变化项中只考虑平均流的贡献是有所欠缺的，这样忽略了波浪Stokes漂对温度的平流输运作用，因此，在混合层温度方程平流输运项中加入Stokes漂流的影响是合理，且必要的。

在温度平流变化项中加入Stokes漂影响，则SST方程变为：

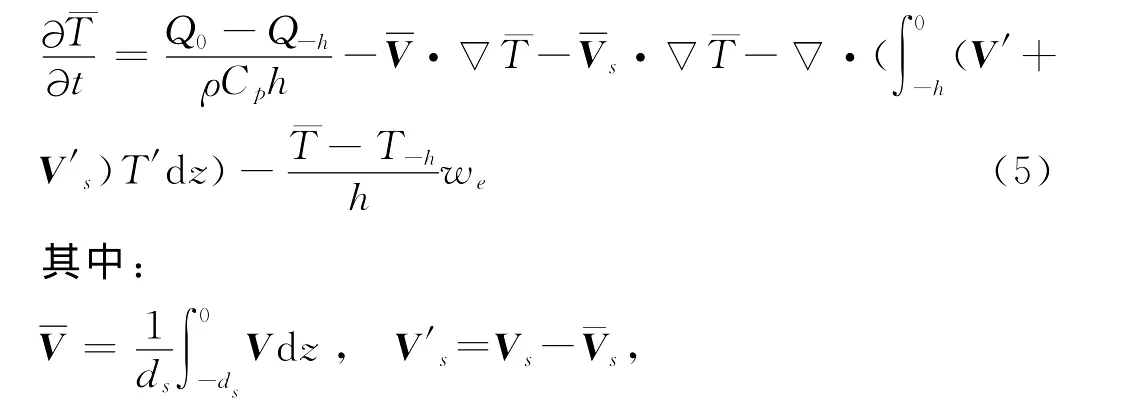
需要指出，方程右侧第3项在计算过程中可以忽略掉，原因是当选取h为混合层深度时，混合层内的流速梯度以及温度梯度较小，另外，为了简化计算的复杂性，可将此小项忽略掉。所以式（5）右侧第3项即为浪致水平输运对混合层平均温度变化的贡献。计算过程中，海水密度ρ取1 025kg·m－3，海水比热Cp取3 944 J（kg℃）－1。

对影响SST变化的几个物理量进行量纲分析，其中Eq，Ec，Es，和Ew分别为：热通量项，海洋平均流项，浪致输运项，以及垂直卷夹项对SST变化的贡献。各物理量的量级由以下式子进行估算：

由已有数据可知，海洋上层热通量量级Q为10，混合层深度量级H为10，混合层内平均流流速量级U为0.01，混合层内Stokes漂流速量级Us为0.001，混合层平均温度量级T为10，水平距离尺度量级L为105，穿越等h面速度量级W为10－5。由此得到各物理量的量级分别为：Eq＝1×10－7，Ec＝1×10－6，Es＝1×10－7，Ew＝1×10－5。

由此可见，在量级上浪致水平输运作用对混合层温度变化的影响Es与其它几个物理量是完全可比的，因此，进一步定量计算Es，并且分析其重要性是必要的。

1.2 数据简介

本文所使用数据包括：

SODA：气候态月平均温度，水平流速。水平分辨率：1°×1°，垂直方向：最大深度4 000 m，分20层，最上11层每层厚度15 m。

NCEP／NCAR Reanalysis：连续63a月平均海面净长波辐射通量，短波辐射通量，感热通量，以及潜热通量，水平分辨率：高斯网格（192×94）88.542°N～88.542°S，0°E～358.125°E。

ECWMF：连续44 a月平均波浪有效波高，平均周期，平均波向。水平分辨率：2.5°×2.5°。

将不同分辨率数据插值到1°×1°的相同网格上，进行进一步的计算。

2 波浪Stokes漂流对SST变化的贡献

2.1 混合层深度h

混合层深度h可由与参考深度处的温度和密度差或者温度和密度梯度进行定义。Brainerd［17］的研究指出，基于温度或密度差值比基于梯度计算的混合层深度结果更理想。所以本文采用与参考深度的温度差的定义方法，取比表层温度低0.5℃的深度作为混合层深度。

利用SODA气候态月平均温度资料获得了全球气候态年平均混合层深度分布。如图1所示，全球年平均混合层深度跨度为10～50 m，在南北半球西风带和赤道区域明显较其它区域深，在赤道区域和北半球高纬度地区年平均混合层深度大约在100 m左右，南半球西风带区域最深能够达到200 m以上。混合层深度的分布特征为，在存在上层强流的区域（赤道区域，西边界流区域），以及高风速区域（南北半球西风带区域），混合层深度较深，其它区域相对较浅。

图1 全球年平均混合层深度分布（单位：m）Fig.1 The distribution of global annual mean mixed layer depth（Unit：m）

2.2 波浪Stokes漂

对于单频深水重力波，其Stokes漂可以表示为：

其中：Us.s为海洋表面Stokes漂的速率；k为单位波数矢量；k为波数；a为振幅；σ为频率。由公式6进行推导，得到用有效波高Hs，平均波周期T表示的Stokes漂，形式为：

Stokes漂影响深度典型值为5～10 m，表示为：

Stokes漂影响深度全球分布特征如图2所示，深度范围为6～13 m，各大洋东侧较大洋西侧的影响深度深，这是由于大洋风浪，涌浪分布特征导致的结果。Chen et al.［18］利用卫星资料和统计理论，对全球风浪、涌浪的分布情况进行了研究，发现大洋东边界存在涌浪加强现象，并称此现象为大洋东边界“涌浪池”。Zhang et al.［19］利用3个新的指标（风－浪相关系数、波龄和涌浪指标）对全球风浪涌浪的分布情况进行了研究，证明了大洋中涌浪存在长期东向强化的趋势，即“涌浪池”的存在性。大洋东侧涌浪占优，波浪平均周期较长，单位长度的波数少，根据式7可知，相对Stokes漂影响深度较大。

根据公式7，8，利用多年平均的ECMWF的波浪数据对Stokes漂进行计算，得到海洋表层Stokes漂全球分布特征（见图3）。海表面Stokes漂速率在南北半球的西风带区域高于其它区域，达到10 cm／s左右，在其它区域较小，大致为4cm／s左右。在影响深度ds上平均的Stokes漂速率（见图4）较海洋表面小，因为随深度增加，Stokes漂速率成指数递减。与海洋表面Stokes漂分布类似，平均Stokes漂速率值在南北半球西风带高风速区域较大，在南半球高纬度区域为2 cm／s左右，最大能够达到8 cm／s；北半球太平洋高纬度区域较南半球小，最大能够达到3cm／s；中低纬度海区大概在0.4～0.8 cm／s范围内。由此可见，年平均Stokes漂分布受风场影响最为显著。

2.3 Stokes漂对SST变化的贡献

Stokes漂对SST变化的贡献即为式（3）中右侧第三项，即：

图5给出了气候态年平均Stokes漂对SST变化贡献的全球分布特征，Es的极值分布于南半球西风带区域，Es正的最大值达到2.677 8×10－6℃／s，负的最大值达到－2.650 3×10－6℃／s。同时北半球，太平洋和大西洋高纬区域，Es值同样高于中低纬区域。可见由于Stokes漂与风场的密切相关特性，在高纬强风速区域Stokes漂对SST的影响最大。在印度洋，太平洋和大西洋3个大洋中，由于印度洋所处纬度的特殊性，并未受到常年存在的强风的影响，所以Es在印度洋表现的区域差异性最小，且量值较小，大约在0.001×10－6℃／s的量级；太平洋与大西洋Es的空间分布特征略有相似，正负最大值均出现在25°N～50°N区域，明显为高风速影响的结果。

图5 年平均Stokes漂对SST变化贡献（单位：℃／s）Fig.5 The annual mean effect of Stokes－drift on the SST variation（Unit：℃／s）

2.4 Stokes漂影响的重要性

比较Es（见图5）与Ec（见图6）可以看出，在全球范围内，量值上，Ec明显比Es大，但二者明显处于可比的量级，平均流水平输运对SST变化的贡献正负极值同样出现在南极南极绕极流区域，Ec正贡献的最大值达到9.854 9×10－6℃／s，Ec负贡献的最大值达到－8.429 2×10－6℃／s。在全球范围内，存在强流的区域，Ec明显大于其它区域。图7给出了Es与Ec比值的等值线图，二者的比值在赤道流区域，西边界流区域较低，浪致平流输运只为平均流水平输运的5%左右；而在南北半球高风速区域，Es所占比例较高，最高能够达到70%；二者全球平均比值为23.43%，由此可见，Stokes漂所导致的对温度的平流输运，相对于平均流对温度的输运并非小量，浪致温度平流输运作用同样重要。

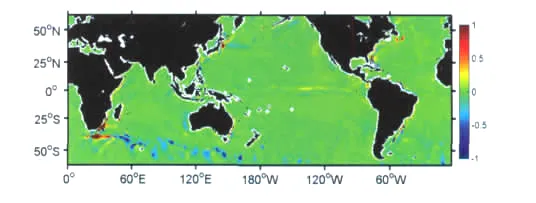
图6 年平均海洋上层平均流对SST变化的贡献（单位：10－6℃／s）Fig.6 The annual mean effect of upper ocean mean current on the SST variation（Unit：10－6℃／s）

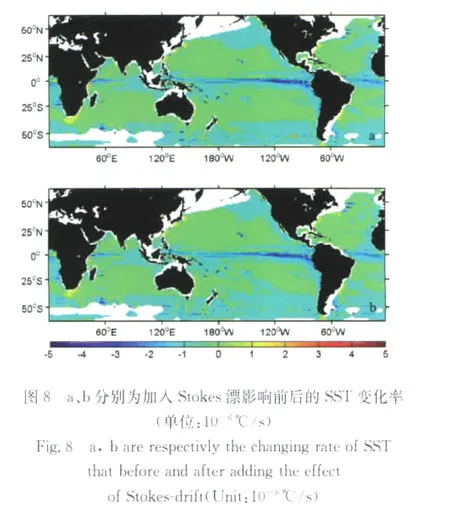
3 结论

本文通过将波浪Stokes漂的平流输运作用加入到海洋混合层温度变化方程中，并在混合层深度上进行积分，研究了浪致水平热输送对混合层温度变化的贡献。计算结果表明，波浪Stokes漂的平流输运作用对混合层温度变化的贡献与平均流的贡献在量值上处于可比的量级，其比值在全球海洋低纬度区域较小，为1%～10%，而在中高纬度区域较大，甚至某些区域能够达到70%。而对于总体SST变化率的影响也较为显著。加入Stokes漂影响后，SST变化率在北半球中高纬度大致表现为增加，最大增加0.4×10－6℃／s，在南半球中高纬度大部分区域表现为减小，最大减小0.35×10－6℃／s；而对于低纬度区域变化相对较小，处于（0.01～0.1）×10－6℃／s范围内。加入Stokes漂影响后SST变化率的变化的全球平均值达到0.077 8×10－6℃／s。而相对SST变化率的全球平均值0.516 2×10－6℃／s，二者比值达到15.07%，并非可忽略的小量，因此，在对于海洋混合层温度计算过程中，考虑波浪Stokes漂的作用是必要的，并且通过在目前的数值计算中考虑波浪的影响，使计算更加接近海洋真实动力学过程，提高计算结果与真实海洋的一致性。通过本文的研究，证实了波浪影响气候变化的可能性，同时也对波浪影响上层海洋温度变化的物理机制进行了初步探讨，即波浪的平流输运作用为混合层温度变化影响机制之一，其作用是不可忽视的。

需要指出，本文所用数据并非同数据集，且数据的分辨率较低，由此会产生一定的误差，但并不影响最终结论。本文只研究了Stokes漂对年平均SST变化率的影响，但对其季节变化等时间分布特征并未进行研究，在进一步的工作中将进行有关时间分布特征的研究。

致谢：感谢王斌，王智峰，毕凡在本文工作中提供的帮助。

［1］ Qiao F L，Yuan Y L，Yang Y Z，et al.，Wave－induced mixing in the upper ocean：Distribution and application in a global ocean circulation model［J］.Geophys Res Lett，2004，31：L11303，doi：10.1029／2004GL019824.

［2］ Qiao F L，Yang Y Z，Xia C S，et al.，The role of surface waves in the Ocean mixed layer［J］.Acta Oceanologica Sinica，2008，27（3），30－37.

［3］ 杨永增，乔方利，夏长水，等.海浪对海洋上层的动量与混合作用分析［J］.海洋科学进展，2003，21（4）：363－368.

［4］ Li S，Song J B，Sun Q.Effect of Stokes drift on upper ocean mixing［J］.Acta Oceanologica Sinica，2008，27（2）：11－20.

［5］ Longuet－Higgins M S.Mass transport in water waves［J］.Phil Trans Roy Soc London，1953，A245：535－581.

［6］ Longuet－Higgins M S.Mass transport in the boundary layer at a free oscillating surface［J］.J Fluid Mech，1960，8：293－306.

［7］ Kenyon K E.Stokes transport［J］.J Geophys Res，1970，75：1133－1135.

［8］ Weber J E.Steady wind－and wave－induced currents in the upper ocean［J］.J Phys Oceanogr，1983，13：524－530.

［9］ Jenkins A D.A theory of steady and variable wind－and wave－induced currents［J］.J Phys Oceanogr，1986，16：1370－1377.

［10］ McWilliams J C，Restrepo J M.The wave－driven ocean circulation［J］.J Phys Oceanogr，1999，29：2523－2540.

［11］ Lane E M.Wave－Current interaction：A comparison of radiationstress and vortex－force representations［J］.J Phys Oceanogr，2006，37，1122－1141

［12］ Wu K J，Yang Z L，Liu B，et al.Wave Energy Input into the Ekman Layer［J］.Science in China Series D：Earth Sciences，2008b，51（1）：134－141.

［13］ 邓增安，吴克俭，于婷.太平洋东边界波浪输运［J］.海洋学报，2007，29（6）：1－9.

［14］ 张坤兰，吴克俭，胡保全，等.北太平洋波浪输运和西边界流的季节变化［J］.海洋湖沼通报，2009，4：17－24.

［15］ Deng Z A，Xie L A.Coupling winds to ocean surface currents over the global ocean［J］.Ocean Modelling，2009，29：261－268.

［16］ Stevenson J W，Niiler P P.Upper ocean heat budget during the Hawaii－to－Tahiti shuttle experiment［J］.J Phys Ocesnogr，1983，13：1894－1907.

［17］ Brainerd K E，Gregg M C.Surface mixed and mixing layer depths［J］.Deep Sea Res I，1995，42（9）：1521－1543.

［18］ Chen G，Chapron B，Ezraty R，et al.A global view of swell and wind sea climate in the ocean by satellite altimeter and scatterometer［J］.J Atmos Oceanic Technol，2002，19：1849－1859.

［19］ Zhang J，Wang W L，Guan C L.Analysis of the global swell distributions using ECMWF re－analysis wind wave data［J］.J Ocean Univ China，2011，10（4）：325－330.

The Influence of Stokes－Drift on the Alteration Ratio of Temperature in the Oceanic Mixed Layer

ZHANG Xiao－Shuang1，2，WU Ke－Jian1，3
（1.College of Physical and Environmental Oceanography，Ocean University of China，Qingdao 266100，China；2.The Key Laboratory of Marine Environmental Information Technology，National Marine Data and Information Service，State Oceanic Administration，Tianjin 300171，China；3.Physical Oceanography Laboratory，Ocean University of China，Qingdao 266003，China）

Adding the influence of Stokes－drift to the advection transport of mixed layer temperature equation to caculate the contribution of Stokes－drift to the mixed layer temperature alteration rate.That is also the contribution to the alteration rate of SST.The results show that the effect of Stokes－drift and the effect of mean current to mixed layer temperature alteration are on a comparable magnitude，the global mean ratio of the two components is 23.43%，and the biggest ratio reach to 70%.In addition，for the total rate of SST change，the effect of Stokes－drift is also remarkable.After adding the effect of Stokes－drift，the changing of globle mean SST alteration rate is 0.0778×10－6℃／s，and the maximum changing reach to 0.989×10－6℃／s，compare to the global mean value of SST alteration rate 0.5162×10－6℃／s，the changing reach to 15.07%，that should not be ignored.Therefore，it is necessary to add the effect of Stokesdrift into the caculation of temperature in mixed layer.

Stokes－drift；mixedlayer；alteration rate of SST；advection transport

P731.22

A

1672－5174（2012）09－001－06

国家自然科学基金项目（40976005，40930844）资助

2011－10－14；

2011－11－17

张晓爽（1984－），女，博士生。E－mail：zhangxs96＠gmail.com

＊＊通讯作者：E－mail：kejianwu＠ouc.edu.cn

责任编辑 庞 旻