新的L-矩阵线性方程组的预条件AOR迭代法

李 园，韩海山

(内蒙古民族大学 数学学院，内蒙古 通辽 028043)

本文考虑如下线性方程组：

Ax=b，

(1)

其中:A∈Rn×n为非奇异矩阵，b∈Rn为已知向量，x∈Rn为未知量.预条件方法通常是找到合适的预条件算子P，将Ax=b等价地转化为如下预条件线性方程组:PAx=Pb，其中P∈Rn为非奇异预条件矩阵.

文献[1]中给出了预条件矩阵为Pα=I+Sα的预条件AOR迭代法，其中:

α是参数.

文献[2]中改进了上述迭代法，给出了预条件矩阵为Pαβ=I+Sαβ的预条件AOR迭代法，该预条件也是文献[3]中预条件的推广，其中:

(2)

α，β是参数，当β=0时，Sαβ=Sα.

本文建立了新的预条件AOR迭代法与文献[1]和文献[2]以及经典的AOR迭代法的比较定理.通过比较定理，得出本文提出的预条件方法比文献[1]和文献[2]以及经典的AOR迭代法更有效.

为方便起见，令A=I-L-U，其中I是单位矩阵，-L和-U分别是矩阵A的严格下三角和严格上三角矩阵，则线性方程组(1)相应的预条件AOR方法的迭代矩阵为：

Lγω=(I-γL)-1[(1-ω)I+(ω-γ)L+ωU]，

(3)

其中：ω和γ是参数，ω≠0.

记本文讨论的预条件线性系统为:

(4)

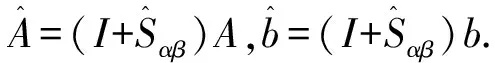
若记SαβU=DS+ES,RL=DR+FR，其中DS和ES分别为SαβU的对角和严格下三角矩阵，DR和FR分别为RL的对角和严格下三角矩阵，则有:

I-L+Sαβ-(U-R+RU)-DS-ES-DR-FR=

(I-DS-DR)-(L+ES+FR-Sαβ)-(U-R+RU)=

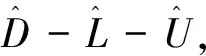
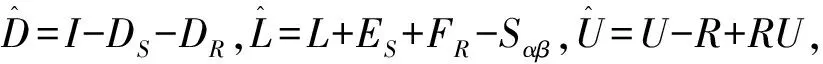
1 预备知识

为方便起见，本文给出如下记号.设A=(aij)∈Rn×n为n×n实矩阵.diag(A)为矩阵A的对角元素aii(i=1,2,…,n)构成的n×n对角矩阵.对于任意矩阵A=(aij)，B=(bij)∈Rn×n，称A≥B，如果对所有i,j=1,2,…,n，成立aij≥bij.若矩阵A的每一个元素aij≥0，i,j=1,2,…,n，则称矩阵矩阵A是非负矩阵，记作A≥0.称A-B≥0当且仅当A≥B.对于n维向量也有类似的定义，ρ(·)表示矩阵的谱半径.

定义1[3]矩阵A=(aij)∈Rn×n，

1)若aij≤0，i≠j，i,j=1,2,…,n，则称矩阵A为Z-矩阵；

2)若A∈Z且aii≥0，i=1,2,…,n，则称A为L-矩阵；

3)若A∈Z非奇异且A-1≥0，则称A为M-矩阵.

定义2[4]设矩阵M∈Rn×n非奇异，矩阵分裂A=M-N称为：

1)收敛的，如果ρ(M-1N)<1；

2)正则分裂，如果M-1≥0且N≥0；

3)弱正则分裂，如果M-1≥0且M-1N≥0；

4)M-分裂，如果M是M-矩阵且N≥0.

定义3[5]矩阵A=(aij)∈Rn×n称为可约的，如果存在n×n阶置换矩阵P，使得:

其中:A11是r×r阶矩阵，A22是(n-r)×(n-r)阶矩阵，1rn.如果矩阵A不是可约的，则称A不可约.

引理1[5](Perron-Frobenius) 若矩阵A=(aij)∈Rn×n为非负不可约矩阵，则:

1)ρ(A)为矩阵A的一个正特征值；

2)对于ρ(A)，相应地存在一个正的特征向量x>0；

3)ρ(A)是矩阵A的一个单特征值；

4)ρ(A)随矩阵A的任一元素增加而增加.

引理2[6]如果矩阵A是一个L-矩阵，则A是M-矩阵当且仅当存在一个正的向量x>0，使得Ax>0.

引理3[7]设A=(aij)∈Rn×n为非负矩阵，则：

1)若存在x≥0，x≠0满足Ax≥αx，则ρ(A)≥α，进一步地，若Ax>αx，则ρ(A)>α；

2)若存在x≥0，x≠0满足Axβx，则ρ(A)≤β，进一步地，若Ax<βx，则ρ(A)<β；

3)若A不可约并且有0≠αx≤Ax≤βx，αx≠Ax和Ax≠βx对某一非负向量x成立，则α<ρ(A)<β且x是一个正向量.

引理4[8]设A=M-N是M-分裂，则ρ(M-1N)<1当且仅当A是非奇异M-矩阵.

2 主要结论

本文的证明需要用到下面的定理：

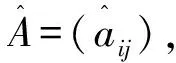
因为A是M-矩阵，aij≤0，i≠j，且aii=1，所以当i=1,2,…,n-1；j=1,2,…,n时，aij-σiai,i+1ai+1,j≤0.

；j=2,…,n-1，

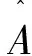
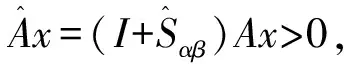
根据定理1，可以建立下面的比较定理：

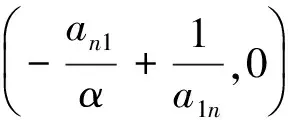
矩阵A的元素满足00(i=1,2,…,n-1)，则有：

(ii)设A=I-L-U是不可约矩阵，因为：

Lγω=(I-γL)-1[(1-ω)I+(ω-γ)L+ωU]=(1-ω)I+ω(1-γ)L+ωU+T，

其中：T=(I-γL)-1γL[ω(1-γ)L+ωU]≥0，可知Lγω是不可约矩阵，由引理1，存在一个向量x>0，使得Lγωx=λx，其中λ=ρ(Lγω)，则有：[(1-ω)I+(ω-γ)L+ωU]x=λ(I-γL)x，

上式等价于： [(1-ω-λ)I+(ω-γ-λγ)L+ωU]x=0

和： (λ-1)(I-γL)x=ω(L+U-I)x，

于是：

(ω-γ+λγ)(L+ES+FR-Sαβ)+ω(U-R+RU)]x=

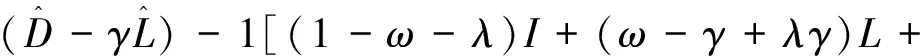
ωU-(1-ω-λ)(DS+DR)+(ω-γ+λγ)(ES+FR-Sαβ)+ω(RU-R)]x=

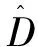
ω(DS+DR+ES+FR-Sαβ+RU-R)]x=

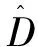
ω(R+Sαβ)(L+U-I)]x=

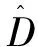
(λ-1)(R+Sαβ)(I-γL)]x=

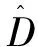
FR-Sαβ-RL)+(λ-1)(R+Sαβ)]x=

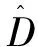
DR-Sαβ)+(λ-1)(R+Sαβ)]x=

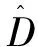
(λ-1)(R+Sαβ)]x=

γ(λ-1)(ES-Sαβ)+(λ-1)(R+Sαβ)]x=

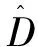
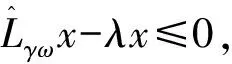
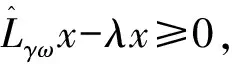
由上述定理可得如下推论：

当ω=γ时，AOR迭代法即为超松弛(SOR)迭代法，相应地有如下结论：

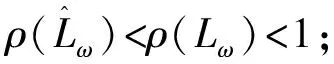
当ω=1，γ=0时，AOR迭代法即为雅可比(Jacobi)迭代法，相应地有如下结论：

3 数值举例

运用文献[2]中的例子，将本文的新算法与已知算法进行比较，来说明新算法更为有效.文献[2]中线性方程组(1)的系数矩阵为：

表1 几种预条件AOR迭代法迭代矩阵谱半径的比较

表2 几种预条件SOR迭代法迭代矩阵谱半径的比较

表3 几种预条件Jacobi迭代法迭代矩阵谱半径的比较

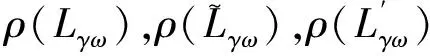
由表1～3，当ω和γ取不同值时，可以看出本文所提出的预条件AOR迭代法、预条件SOR迭代法和Jacobi迭代法的收敛速度更快，这也正好验证了本文的结论.

[1] Li Y T，Li C X，Wu S L.Improvements of preconditioned AOR iterative methods forL-matrices[J].J Comput Appl Math，2007，206：656-665.

[2] Wang H J，Li Y T.A New preconditioned AOR iterative methods forL-matrices[J]. J Comput Appl Math，2009，229：47-53.

[3] Li Y T，Wang H J，Zhang C Y. New preconditioned AOR iterative methods for Linear System[J]. SEAMS Bull Math，2007，31：295-306.

[4] Young D M. Iterative Solution of Large Linear Systems[M].London：Academic Press，NY，1971.

[5] Varga R S. Matrix Iterative Analysis[M].NY：Prentice-Hall，Englewood Cliffs，1962.

[6] 陈景良，陈向晖.特殊矩阵[M].北京：清华大学出版社，2001.

[7] Gunawardena A D，Jain S K，Snyder L.Modified Iterative Method for Consintent Linear System[J].Linear Algebra Appl，1991，154/156：123-143.

[8] Andreas F，Daniel B S.H-splitting and two-stage iterative methods[J].Numer Math，1992，63：345-356.