基于改进联合卡尔曼滤波算法的列车测速信息融合*

严建鹏，陈小强，侯 涛

(兰州交通大学自动化与电气工程学院，甘肃兰州730070)

我国高速铁路动车组列车普遍采用车轮速度传感器与多普勒测速雷达相结合的方式来测量列车运行速度。速度传感器在高速时测量更加精确，雷达则在低速和车轮发生空转或打滑时测量更加精确。同时使用这2种设备测速，可以实现优势互补，得到较单一测速传感器更加精确的列车运行速度。为了提高测速系统的可靠性，每套车载设备配备了2个速度传感器和2个雷达，并由2套车载设备共享［1］。四路传感器测量信息同时送到2个测速信息融合单元进行处理，每个车载测速单元就构成了1个多路速度传感器信息融合单元。由于传感器在测量过程和信息传输过程中不可避免地会受到外来干扰和内部噪声的影响(例如列车牵引变化、车轮打滑、空转、磨损、外界气候条件影响、传感器自身测量误差以及脉冲采集误差等因素)，使得测量精度下降，而且容易造成误差的累计，危及行车安全。因此，测速信息融合处理单元需要将速度传感器和测速雷达测量的数据进行融合和误差修正，消除噪声干扰，以获得精确的列车运行速度。基于联合卡尔曼滤波算法的多传感器信息融合技术就是以多个测速传感器测量信息作为输入，采用先分散处理，再全局融合的思想，通过时间更新和观测更新，进行算法递推，并以融合后的全局最优估计值作为系统的输出［2］。该方法具有设计灵活，计算量小、容错性能好等特点，不仅能提高融合精度，而且在某一传感器故障的状态下仍然能够保证输出信号的精确度，是解决问题的优选方案。黄卫中等［3］采用联合卡尔曼滤波理论思想，分析了多路速度传感器信息融合过程。本文在此基础上，进一步研究其提出的测速测距算法策略，对联合卡尔曼滤波算法在噪声统计特性发生变化情况下的不足，引入自适应联合卡尔曼滤波算法对其进行改进，以进一步提高测速精度，使系统具有更强的适应能力。

1 联合卡尔曼滤波算法

1．1 系统模型与结构

因为速度传感器与测速雷达的输出信号均为离散型高频脉冲信号，列车加速度变化与之相比，是一个缓慢的过程。因此，在1个采样周期内，可以将列车运行过程看作是匀加速运动，列车牵引力对系统状态的输入噪声向量为0。根据离散系统特性，列车测速系统数学模型为:

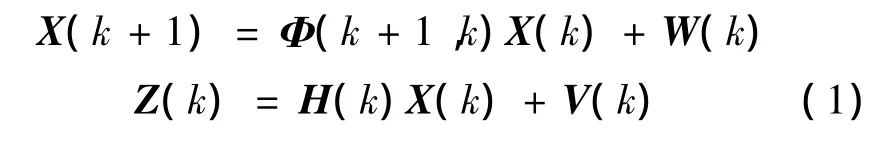
其中:k为传感器离散采样时刻;X(k)为k时刻系统的状态向量;Z(k)为系统的观测向量;W(k)为系统的随机噪声向量;V(k)为系统的观测噪声向量;Φ(k+1，k)为系统的状态转移矩阵;H(k)为系统的测量矩阵［1，4－7］。其噪声统计特性为:

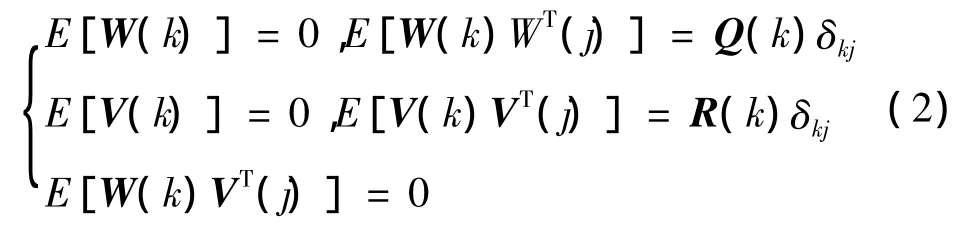
其中:Q(k)为过程噪声W(k)的非负定方差矩阵，R(k)为观测噪声V(k)的正定方差矩阵;δkj为克罗内克函数，并定义为:

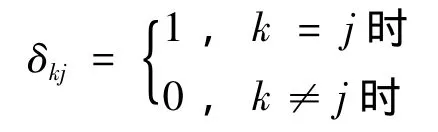
其自变量(输入值)一般是2个整数。

基于联合卡尔曼滤波算法的列车测速信息融合系统由1个主滤波器和4个子滤波器(对应四路测速传感器)构成，子滤波器之间相互独立、并行工作。四路测速传感器向测速信息融合单元提供原始测量数据，各子滤波器将传感器测量数据进行局部滤波，将得到的局部状态估计和估计误差送给主滤波器，主滤波器再将局部滤波结果进行融合，得到全局最优估计。在此过程中，主滤波器根据信息分配原则，将初始状态信息、公共测量信息及动态噪声信息作为先验信息，分配给各子滤波器，以得到各局部最优融合估计［4－6］。如图1所示，其中下标m和g分别代表主滤波器和全局融合结果。

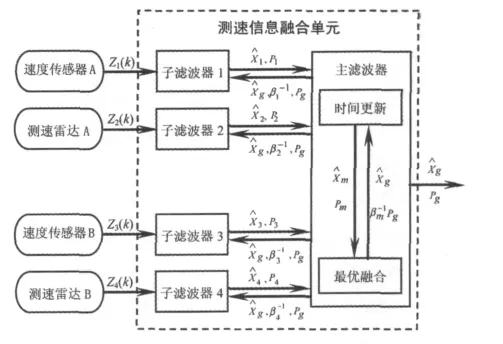
图1 基于联合卡尔曼滤波算法的多路测速传感器融合结构图Fig．1 Structure diagram of multi speed sensor measurement information fusion based on federated Kalman filter algorithm

1．2 算法过程

由图1可知，融合后的全局估计值 ^Xg及其相应的估计误差方差矩阵Pg被放大为后再反馈到子滤波器，以重置子滤波器的估计值。同时，主滤波器的估计误差方差矩阵重置为全局估计误差方差矩阵的倍，即其中βi(i=1，2，…，n，m)称为信息分配系数，0 ≤ βi≤1，需满足信息守恒原理

假定起始时刻全局状态的初始值为X0，其协方差矩阵为P0，系统协方差矩阵为Q0。设，Qi和Pi为子滤波器的状态估计向量、系统协方差阵和状态向量协方差阵，，Qm，Pm为主滤波器的状态估计向量、系统协方差阵和状态向量协方差阵。其中i=1，2，3，4;根据联合滤波算法原理，设 ^X(k+1)为k+1时刻系统的最优状态估计，则第i个子滤波器的系统状态方程和量测方程为:

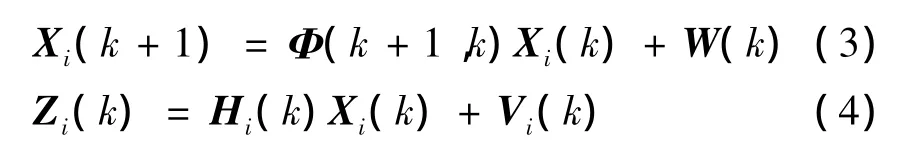
滤波器初始状态条件规定为:

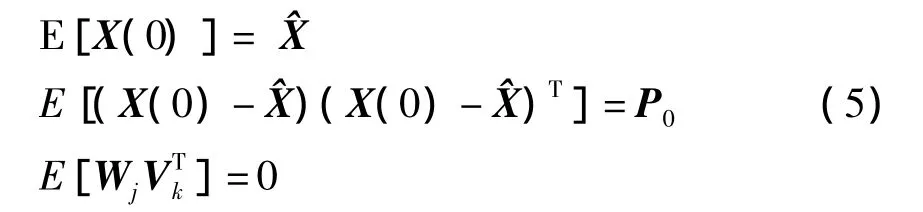
由(3)式可知:过程噪声越弱，系统的状态方程就越精确，状态方程的信息量与其过程噪声的方差(或协方差)成反比。因此，状态方程的信息量可以表示为过程噪声方差矩阵的逆Q－1，状态初值的信息量可以表示为初值估计的协方差矩阵的逆，观测方程的信息量可以表示为观测噪声方差矩阵的逆R－1。同时，状态估计的信息量用P－1来表示。联合卡尔曼滤波算法过程如下［4－5，7－8］。

(1)信息分配过程为:

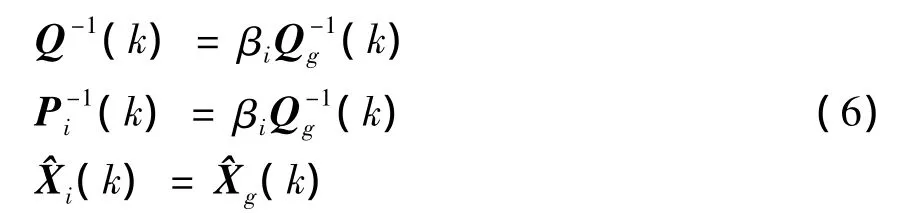
(2)时间更新算法:

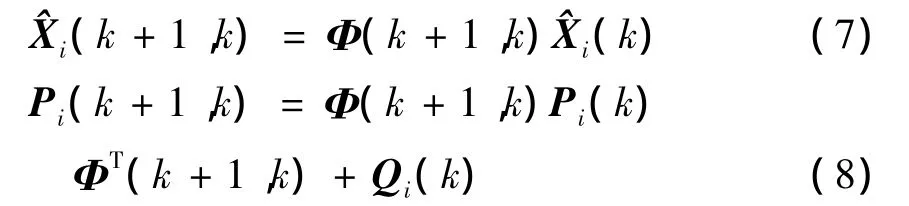
(3)量测更新算法:

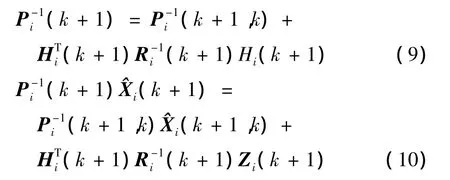
(4)信息融合全局最优估计为:

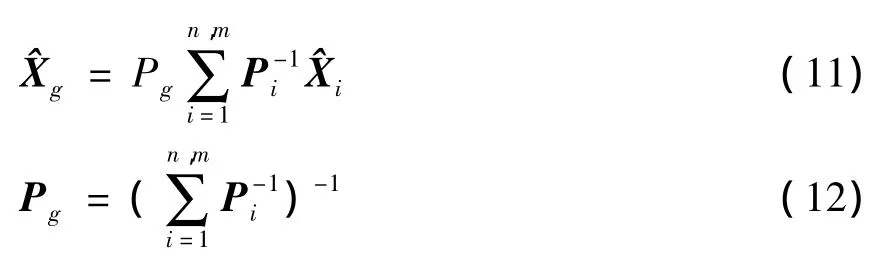
1．3 存在问题

基于联合卡尔曼滤波算法利用了传感器之间噪声或者误差相抵的特性，其结果在理论上更接近列车速度的真实值，但是要求系统具有准确的数学模型和确切的噪声统计特性。而在实际的列车运行过程中，系统过程噪声方差矩阵Q和观测噪声方差矩阵R并不能提前知道，因此，在噪声模型不确切的情况下进行滤波，可能会引起滤波发散，使系统融合精度下降［1，9－10］。同时，由于系统误差和测量误差会随时间和环境的变化而变化，即系统过程噪声方差矩阵Q和测量噪声方差矩阵R发生变化，联合滤波系统由于缺乏系统噪声和测量噪声的先验知识而导致滤波结果出现发散，滤波精度下降。这对于安全可靠性要求极高的高速列车测速系统来讲，是不容许的。为了更好地实现对噪声信号的过滤，需要引入自适应滤波算法对联合卡尔曼滤波算法进行改进，以提高测速系统对环境的适应能力。

2 联合卡尔曼滤波算法的自适应改进

改进的联合卡尔曼滤波算法基本思想是在各子滤波器中增加各传感器噪声估计，在主滤波器中增加系统噪声估计，对系统过程噪声和测量噪声的统计特性实时进行估计和修正，以期达到降低模型误差、抑制滤波发散、提高滤波精度的目的。其算法基本过程如下。

(1)信息分配:

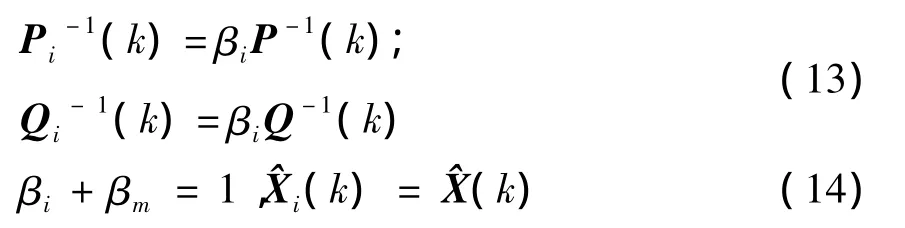
(2) 时间更新:

(3)测量更新(只在子滤波器中进行):

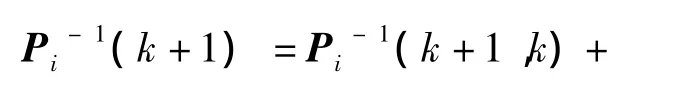
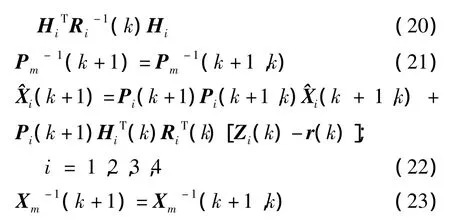
(4)测速信息的融合:

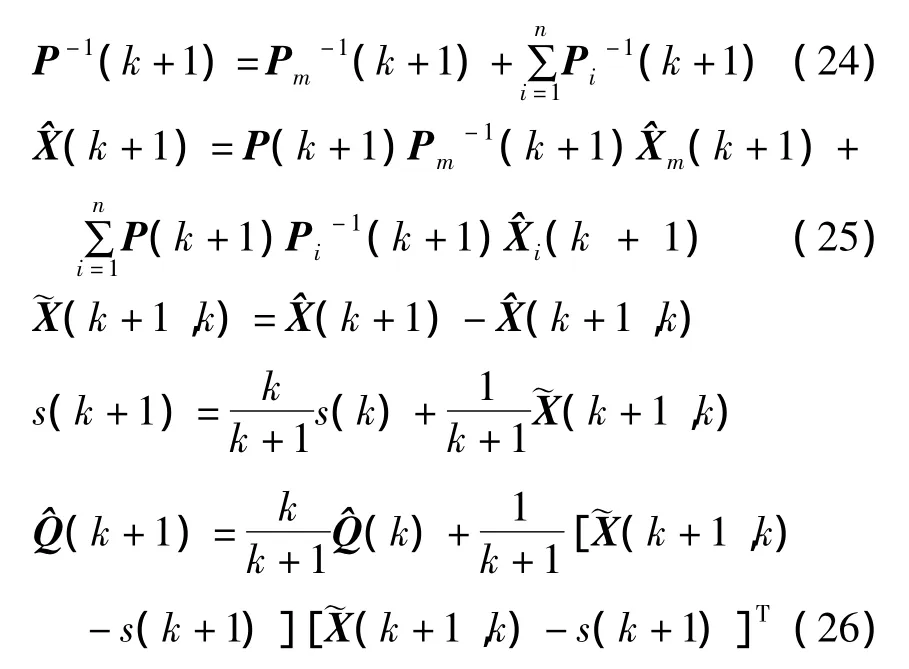
为了进一步清楚的展示该算法，绘制了自适应联合卡尔曼滤波算法结构图，如图2所示。图中带黑圈的序号代表了算法的执行顺序，小括号内的数字代表了具体执行的表达式，箭头所指为信息的流动方向。

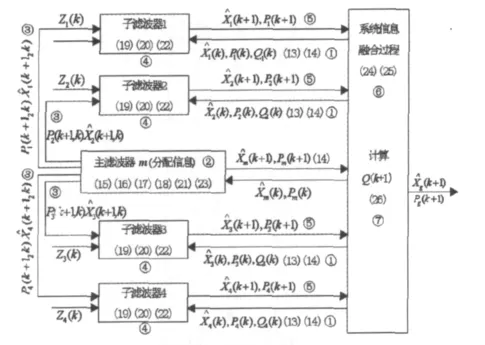
图2 自适应联合卡尔曼滤波算法结构图Fig．2 Structure diagram of adaptive federated Kalman filter algorithm

3 仿真分析

在实验室利用MATLAB仿真软件对改进前后的两种算法进行相应的数值仿真。考虑到测速系统需满足部分测速传感器发生故障时，系统仍要保持较高的容错性能，选取信息分配系数βm=0，β1同时考虑到测速传感器的性能和列车测速系统的实时性要求，选取适当的系统采样频率及初始值，并使改进前后的两种算法的基本参数取值保持一致。采样次数设为1 000次时的仿真结果如图3～4所示。从图3可以看出，四路测速传感器单独进行测量时，测得的列车速度值曲线波动较大，而经过联合滤波处理后的速度值曲线波动明显变小，且基本呈稳定变化趋势。图4所示为运用改进的自适应联合卡尔曼滤波算法得到的融合效果图，与图3所示的融合结果相比，改进后的滤波结果更加稳定，精度比改进前更高，证实了采用改进的自适应算法使联合卡尔曼滤波算法的优越性得到充分的发挥，达到了消除噪声干扰、提高测速精度的目的，并且系统具有良好的稳定性。

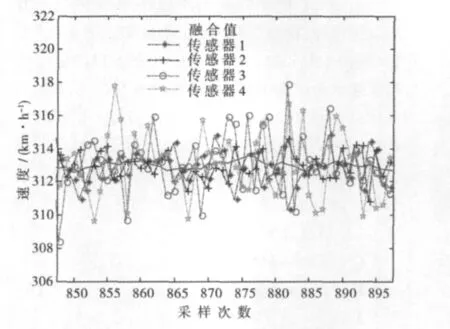
图3 基于联合卡尔曼滤波算法的融合效果图Fig．3 Fusion effect diagram based on federated Kalman filter algorithm

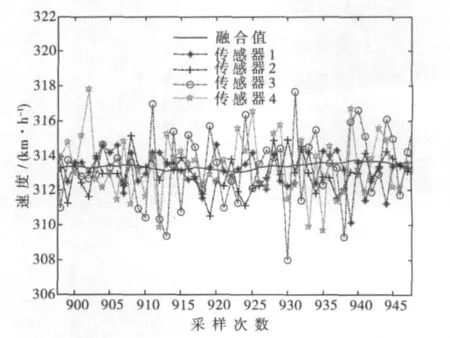
图4 基于自适应联合卡尔曼滤波算法的融合效果图Fig．4 Fusion effect diagram based on adaptive federated Kalman filter algorithm

4 结论

(1)针对联合卡尔曼滤波系统由于缺乏噪声先验知识而导致滤波精度下降的问题，将自适应联合卡尔曼滤波算法应用于列车测速系统中，提高了测速精度，使测速系统具有更好的适应能力。在此基础上，车载设备将融合后的列车速度进行积分，可计算出列车的走行距离。

(2)基于自适应联合卡尔曼滤波的列车测速系统，信息分配系数β取值不同，会影响测速信息融合系统的滤波精度和容错性能。因此，下一步工作是根据传感器测量精度和系统技术指标，对信息分配系数进行优化选取，使系统融合精度和容错性能达到最优。

［1］付梦印，邓志红，闫莉萍．Kalman滤波理论及其在导航系统中的应用［M］．2版．北京:科学出版社，2010．FU Meng-yin，DENG Zhi-hong，YAN Li-ping．Kalman filtering theory and its application in the navigation system［M］．2 nd ed．Beijing:Science Press，2010．

［2］刘朝英，莫志松．京津城际高速铁路信号系统集成［M］．北京:中国铁道出版社，2010．LIU Chao-ying，MO Zhi-song．Signal system integration of Beijing－ Tianjin Intercity Railway［M］．Beijing:China Railway Publishing House，2010．

［3］黄卫中，季学胜，刘 岭，等．CTCS－3级列控车载设备高速适应性关键技术［J］．中国铁道科学，2010，31(3):87－91．HUANG Wei-zhong，JI Xue-sheng，LIU Ling，et al．The key technology of CTCS－3 train control on－vehicle equipment high speed adaptability［J］．China Railway Science，2010，31(3):87 －91．

［4］崔平远，黄晓瑞．基于联合卡尔曼滤波的多传感器信息融合算法及其应用［J］．电机与控制学报，2001，5(3):204－207．CUI Ping-yuan，HUANG Xiao-rui．Multi－ sensor information fusion algorithm based on federal Kalman filter and application［J］．Electric Machines and Control，2001，5(3):204－207．

［5］刘瑞华，刘建业．联邦滤波信息分配新方法［J］．中国惯性技术学报，2001，9(2):28 －32．LIU Rui-hua，LIU Jian-ye．A new method of information－ sharing in federated filter［J］．Journal of Chinese Inertial Technology，2001，9(2):28 －32．

［6］陈玉坤，司锡才，李志刚．联合卡尔曼滤波在多传感器信息融合技术中的应用［J］．弹箭与制导学报，2005，25(4):946－952．CHEN Yu-kong，SI Xi-cai，LI Zhi-gang．Federal Kalman filter and its application to multi－sensor information fusion technology［J］．Journal of Projectiles，Rockets，Missiles and Guidance，2005，25(4):946 －952．

［7］付海峰，刘华伟，张宗麟．联邦滤波器公共信息分配方法［J］．火力与指挥控制，2006，31(8):56 －58．FU Hai-feng，LIU Hua-wei，ZHANG Zong-lin．Methods of public information sharing in federated filter［J］．Fire Control and Command Control．2006，31(8):56 －58．

［8］魏福领，毛 征，王亚丽，等．联合卡尔曼滤波在目标数据融合中的应用［C］//中国仪器仪表学会第九届青年学术会议论文集．2007:393－395．WEI Fu-ling，MAO Zheng，WANG Ya-li，et al．Application of federated Kalman filter in target data fusion［C］//Chinese Instruments to Learn the Ninth Youth Academic Conference Proceedings．2007:393 －395．

［9］邱 凯，荣 军，陈天如，等．基于信息补偿的自适应联邦滤波算法［J］．数据采集与处理．2007，22(3):331－335．QIU Kai，RONG Jun，CHEN Tian-ru，et al．Adaptive federated Kalman filtering algorithm with information compensation［J］．Journal of Data Acquisition ＆ Processing，2007，22(3):331 －335．

［10］肖远龙，曾 超．基于自适应Kalman滤波算法的联邦滤波器［J］．火力指挥与控制．2008，33(12):88－94．XIAO Yuan-long，ZENG Chao．The study of federated filter based on the adaptive Kalman filtering algorithm［J］．Fire Control and Command Control，2008，33(12):88－94．