考虑支路路段双向车流相互影响的单向交通组织优化*

史 峰，王英姿，2，徐光明，秦 进

(1．中南大学 交通运输工程学院，湖南 长沙410075;2．湖南大学 土木工程学院，湖南长沙410082)

由于城市的集聚效应和人类活动趋于频繁，城市交通需求日益增加，虽然大力发展公共交通、鼓励公交出行，但城市汽车保有量的不断攀升导致城市道路网络负荷难以承受，有限的土地资源使得城市道路难于满足快速增长的交通需求［1－2］。为了有效解决城市交通拥堵问题，除了适当抑制小汽车保有量的增长、完善城市道路网络外，提高交通组织水平也是十分有效的解决方案。单向交通组织就是缓解城市交通压力的有效措施，对改善城市交通状况具有重要作用。不少学者研究了城市道路单向交通组织问题，如:Robbins［3］研究单向交通组织下城市任意2点之间的通达性;Kim等［4－5］在研究快速疏散问题时，运用单向交通组织方法研究多源点疏散的最少疏散时间;严新平等［6］也运用单向交通组织方法研究大型活动后的交通疏导问题，魏广奇［7］从道路公平性的角度，寻找车辆绕行距离最短的单向交通组织方案;史峰等［8－9］以降低路段饱和度为目标优化单向交通组织方案，并在支路网络改扩建中得到应用;Long等［10］建立优化单向交通组织方案的双层规划模型，上层规划降低路段负荷、提高道路公平性，下层规划保证网络车流达到用户均衡。然而，上述优化方法的网络车流均衡分析中，总是基于支路路段双向车流分道行驶的假设进行交通分配的。事实上，支路路段并不具备分道行驶的条件，双向车流通过不分道行驶还能双向协调使用路段通行能力，当然，双向不分道也使得双向车流相互影响而降低行驶速度。Wang等［11］利用元胞自动机模型模拟分析了支路路段通行能力，获得不分道行驶的支路路段不同方向流量分布下路段通行能力、车辆平均速度与路段宽度之间的关系曲线，以及不同方向流量比例分布下主辅方向饱和流量、车辆平均速度与路段宽度之间的关系曲线。史峰等［8－9］进一步提出的支路路段通行能力依赖于路段宽度、单车道通行能力、双向流量比例等因素的近似解析公式，扩展了支路路段费用表达式，建立的含支路路段的交通网络均衡模型，拓展了常规交通网络均衡分析的交通分配算法。本文在上述研究成果的基础上，以单行交通组织方案为决策，以交通负荷和道路公平性为优化目标，考虑支路双向车流相互影响的因素进行交通分配，构建城市单向交通组织的双层规划模型。选择饱和度较高的一些路段作为单向行车的候选路段集，以此为搜索邻域设计求解模型的模拟退火算法。由于在交通分配时考虑了支路路段双向车流的影响，所获得的单向交通组织方案更具合理性。

1 单向交通组织中支路双向车流的影响分析

在单向交通组织优化的交通分配中，常规处理手法假设那些双向行驶支路路段总是双向分道行驶的，并且双向具有相同的通行能力。由文献［11］，只有在支路路段的双向流量相当时，这种假设才是合理的。但很多情形并不是这样，如与干道邻近且平行的支路上的双向流量通常并不对称，与干道反方向的交通需求通常较大，而同方向的交通需求通常较小。

双向需求的不对称性对交通分配中双向分道行驶的假设提出异议，由于事先并不知道双向车流的比例，所以只能假设双向具有相同的能力值，这个值如果设得太大，可能导致双向流量之和太大而使得路段无法承载，如果设得太小，可能导致一个方向的通行能力闲置、另一个方向的需求过大而得不到满足，使得路段整体通行能力浪费。

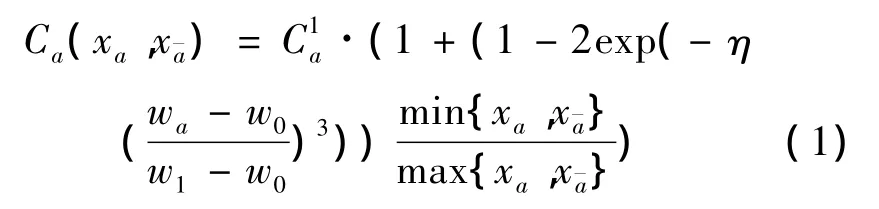
其中:xa和x分别为支路路段a和反向路段的流量;为路段a的单向(单车道)通行能力;系数η，w0，w1为参数;通常取 η =ln2，w0=3．6，w1=5．0，wa为路段a所在道路的宽度。从式(1)中的可以看出:通行能力 Ca(xa，x)依赖于双向流量的比例。支路路段a上的双向流量之和xa+x受到式(1)表示的通行能力的制约，同时xa和x之间也具有一定的调剂功能。

在单向交通组织优化过程中，若能在考虑支路路段双向车流相互影响下进行交通网络均衡分配，将与实际交通状况更加吻合。

2 基于单向交通组织方案的交通均衡分析

下面结合单向交通组织优化的特点，阐述基于支路路段双向车流相互影响的交通网络均衡分析方法。

在城市道路网络N=(V，A∪B)中，节点集V={v1，v2，…，vn}，干道路段集 AB 中各路段均为有向弧，表示分道行驶路段;支路路段集B中各路段均为无向边，是否单行及单行方向待定。路段长度为l(a)，a∈A∪B。节点r至节点s的交通需求为qrs。路段a∈A的通行能力为Ca，a∈B的单向(单车道)通行能力为。

对于a=［vi，vj］∈B，假设i＜ j，记d(a)为单向行车决策变量:

由此获得单行交通组织方案D={d(a)，a∈B}，不同的单行交通组织方案D确定不同的行车网络，记D所确定的行车网络为ND=(V，A∪BD∪B0)，其中:BD为单行路段集，B0为不分道双向行驶路段集，

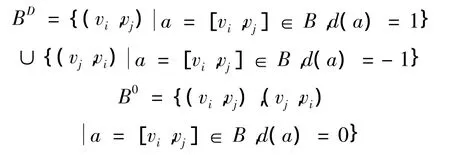
相应地，a=(vi，vj)∈A∪BD∪B0的通行能力可描述如下:

当a∈A时，通行能力为C(a)=Ca;

当a∈BD时，通行能力为C(a)=C1a;

当a∈B0时，a的流量xa和反向路段a的流量 xa之和 xa+xa的限制通行能力为 Ca(xa，xa)。

对于路段a∈A∪BD，行驶时间采用BPR函数ta(xa);对于路段a∈B0，行驶时间采用BPR函数的如下拓展形式:

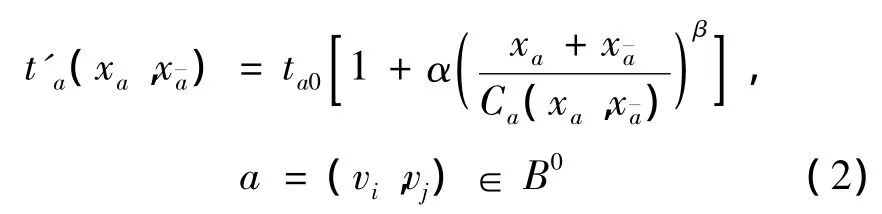
其中:ta0为路段a的零流行驶时间(ta0=t);α和β为参数。

对于O－D对(r，s)∈RS，记Krs为行车网络ND中点对(r，s)之间的全体路径集为点对 (r，s)之间路径k上的流量，为点对(r，s)之间路径k的费用。基于单向交通组织的均衡交通分配模型如下:

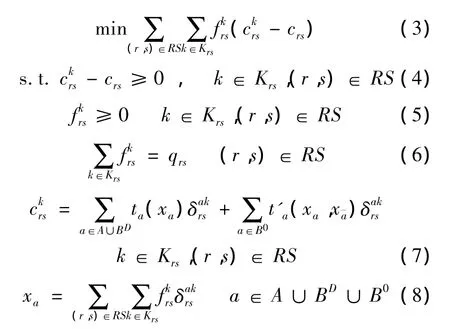
3 单向交通组织的双层规划优化模型与求解思想

为了衡量交通负荷，采用饱和度超限量来描述。对于路段 a∈ A∪ BD，饱和度为 S(a)=对于路段 a∈ B0，饱和度为 S(a)=对于路段a∈A∪BD∪B0，引入保持“畅通”的最大饱和度 S0(a)，饱和度超限量为max{S(a)－S0(a)，0}，记干道平均饱和度超限量为

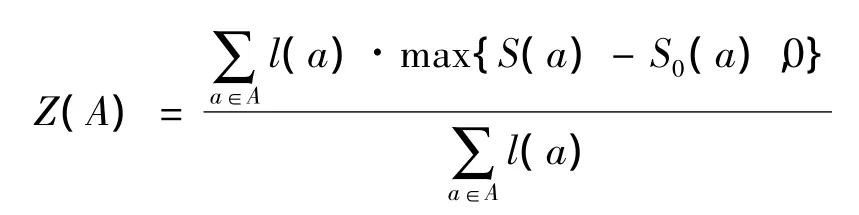
支路平均饱和度超限量为

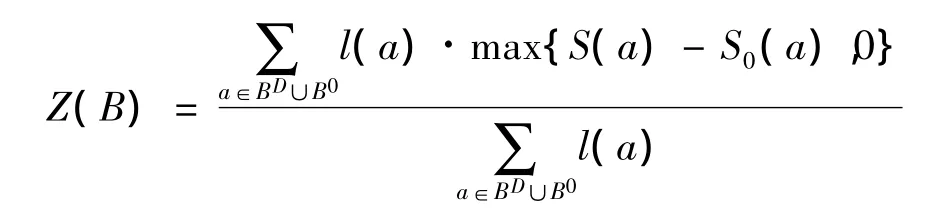
交通负荷的评价就是将干道和支路的平均饱和度超限量最小化，尽可能使得网络畅通。

为了衡量道路公平性，采用绕道系数来衡量。所谓绕道系数就是实施单向交通组织前后的最短里程的相对差，即点对(r，s)在原始路网N中的最短路长lrs与单向交通组织方案D对应行车网络ND中的最短路长确定的差的比例记平均绕道系数为:

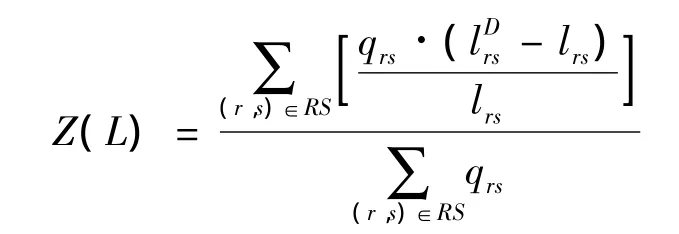
道路公平性的评价就是将平均绕道系数最小化，尽可能使得单向交通组织方案能够有效实施。

综上所述，构建如下考虑支路路段双向车流相互影响的单向交通组织优化方案D的双层规划模型，其中上层规划为:

其中路段流量xa，a∈A∪BD∪B0满足下层规划模型(3)～(8);最短路长，(r，s)∈ RS 分别满足下层规划模型:

从形式上来看，每一条最短路长都用一个数学规划(14)来描述，实际上对于同一个单向交通组织方案D，只需对行车网络ND一次性求出所有最短路。

在实际工程应用中，可以将上述规划不同目标赋予不同的权重参数，将多目标(9～(10)化为如下单目标进行优化:

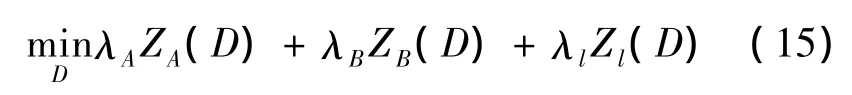
对饱和度超限量较高的路段实施单向交通组织通常是有利的，可以选择饱和度超限量相对高的一些路段构成搜索邻域，从中选择路段实施单向交通组织，由此构建模拟退火算法求解双层规划模型［10］。

4 计算分析

下面对照Long［10］的算例，用本文的优化方法求解单向交通组织方案。由于2种方法需要的数据稍微存在一些差异，这里从原算例相应地估算支路路段的宽度。

含支路路段的网络如图1所示，由17个节点构成，所有实线段为主干道路段，所有细线段为支路路段。保持干道“畅通”的最大饱和度S(a)=0．85，支路“畅通”的最大饱和度 S(a)=0．75，支路路段的单向(单车道)通行能力=800 pcu/h。其他相关数据见表1～3。

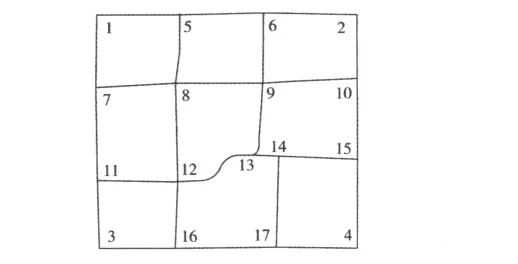
图1 算例网络Fig．1 The test network

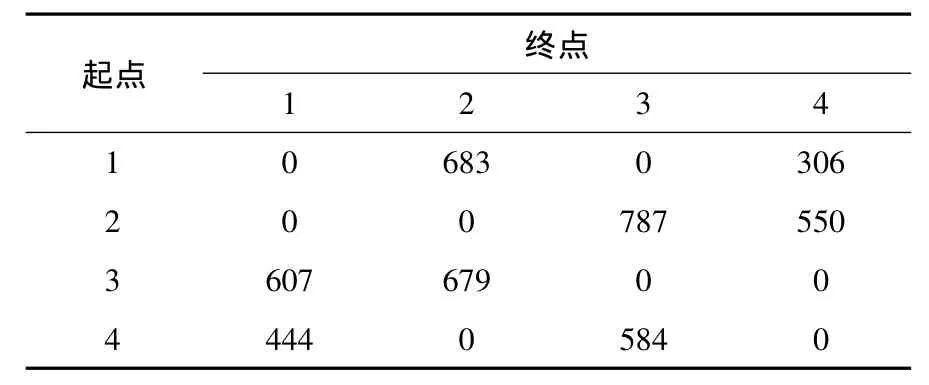
表1 交通需求Table 1 Traffic demands pcu/h

若所有路段均不采用单向交通组织，则干道饱和度为0，支路饱和度为0．1316，超限的支路路段数为6，平均绕道系数为0。若固定λA=λB=1，对于不同的绕道权重λl，利用考虑支路路段双向车流相互影响的单向交通组织优化方法，求解出若干优化方案，对于 λl属于［0．0，0．3］，(0．3，4．0］，(4．0，∞)的3种情形，每一种情形都具有相同的干道和支路饱和度平均超限量、每车平均绕行系数等目标函数值，但对应很多种不同的单向交通组织方案。从中选择3个典型方案如图2所示(箭头表示支路路段单行方向，无箭头路段为双向行驶)，相应的评价指标如表4和表5所示。

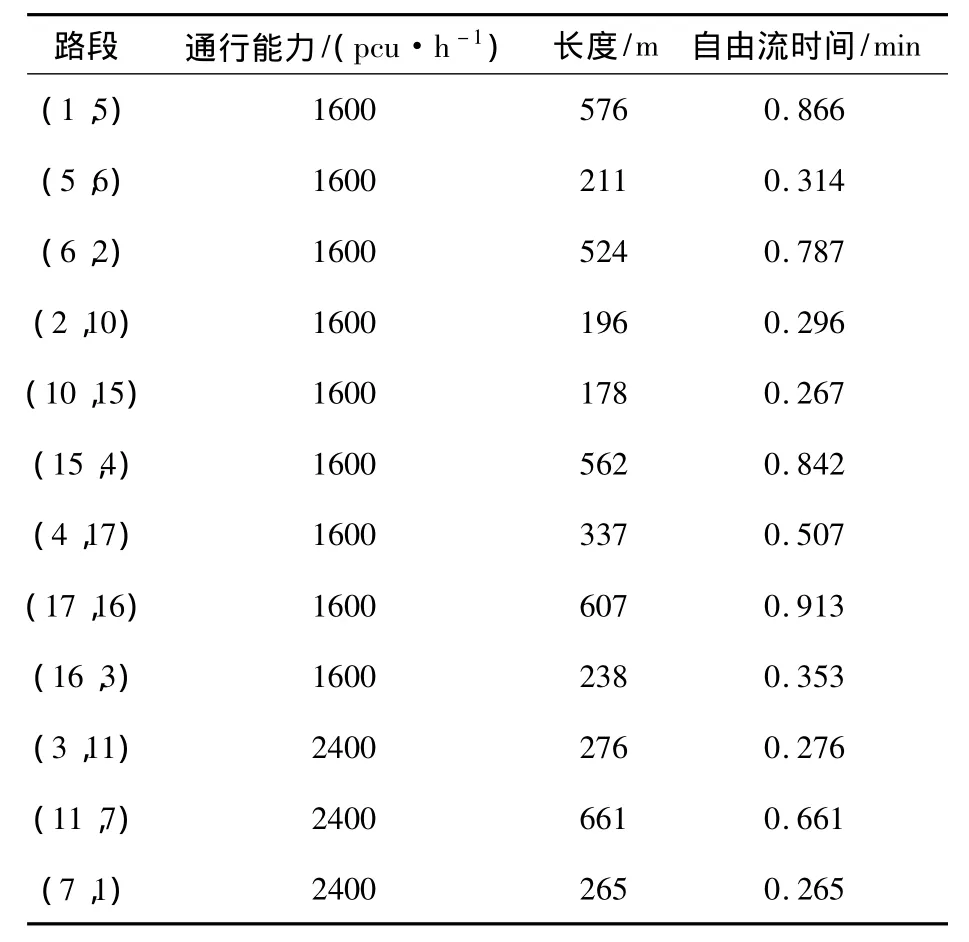
表2 干道路段的主要参数Table 2 Properties of arterial road sections

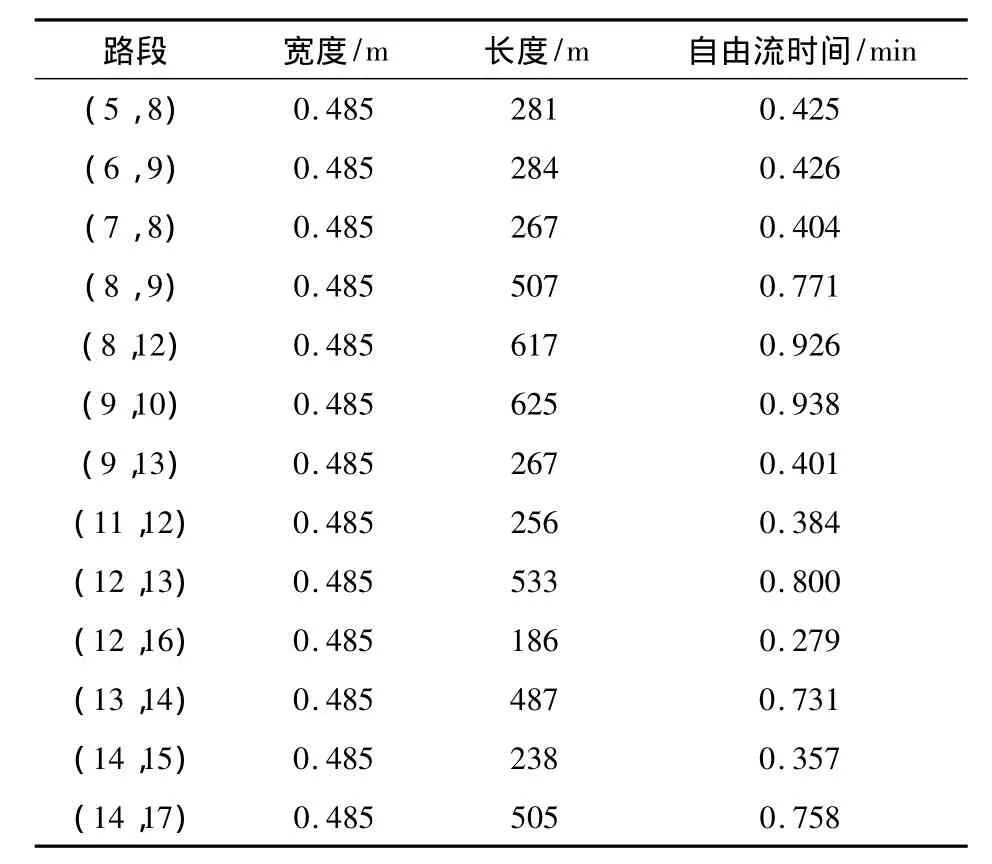
表3 支线路段的主要参数Table 3 Properties of branch road sections

当λl∈(4．0，∞)时，优化方案3优于不采用单向交通组织方案的各项指标，λl减小至(0．3，4.0］时，支路饱和度平均超限量降为0，但干道饱和度平均超限量增加至0．004 1，绕行系数增加至0.007 2;λl进一步减小至［0．0，0．3］时，干道和支路饱和度平均超限量均降为0，但绕行系数增加至0.025 1。这3个典型方案的超限路段数(见表5)分别为0，1或2。

图2 各方案下路网结构比较Fig．2 Comparison of satisfactory road networks

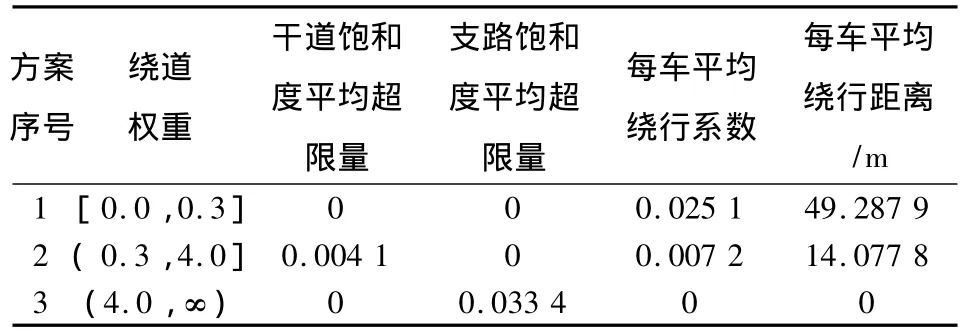
表4 考虑支路双向车流影响的单向交通组织方案的评价指标Table 4 Measurement indexes of one－way traffic organization plan with bi－directional flow’s effect of local road

表5 单向交通组织方案的各超限路段数Table 5 Over－saturation road section numbers of one－way traffic organization plan

另外，与Long［10］的几个典型方案相比，由于考虑了支路双向车流的影响(按照模型(3)～(8)进行交通分配)，关于目标函数(9)～(11)具有明显的优越性。

5 结论

(1)考虑道路负荷与公平性的单向交通组织优化可描述为一个一主多从的双层规划，其中上层规划以单行交通组织方案为决策，通过最小化路段饱和度超限量来降低道路负荷，通过最小化车辆绕行系数来提高公平性。在给定单行交通组织方案条件下，路段流量和任意2点之间的最短路都分别满足相应的下层规划。

(2)双层规划可用模拟退火算法求解，考虑支路路段双向车流相互影响的均衡交通分配方法所求解的路段流量与实际状况更为吻合，虽然每一个点对之间的最短路都描述为一个下层规划，但给定单行交通组织方案的所有最短路可一次性求解获得。

(3)考虑支路路段双向车流相互影响的单向交通组织优化方法明显优于支路路段通行能力等量划分为双向分道行驶的传统优化方法。

［1］Downs A．Smart growth:Why we discuss it more than we do it［J］．Journal of the American Planning Association，2005，71(4):367－378．

［2］Wang Y，Liu W M，Li Y H．Research on relationships between road infrastructure and traffic demand based on granger causality test［J］．Science Technology and Engineering．2008，8(4):1723－1726．

［3］Robbins H E．A theorem on graphs with an application to a problem of traffic control［J］．American Math Monthly，1939(46):281－283．

［4］Kim S，Shekhar S．Contraflow network reconfiguration for evacuation planning:A summary of results［C］//Proceeding of the 13rd Annual ACM International Workshop on Geographic Information Systems．New York:ACM Press，2005．

［5］ Kim S，Shekhar S．Contraflow transportation network reconfiguration for evacuation route planning［J］．IEEE Transaction on Knowledge and Data Engineering，2008，20(8):1115－1129．

［6］严新平，吕超能，等．大型活动后车道单行优化的双层规划［J］．西南交通大学学报，2009，44(1):112－117．YAN Xin-ping，Lü Chao-neng，et al．Bi－ level programming for optimization of contraflow lanes after massive activities［J］．Journal of Southwest Jiao Tong University，2009，44(1):112－117．

［7］魏广奇．城市单向道路定向方法研究［D］．长沙:长沙理工大学，2005．WEI Guang-qi．Research on the directional method of one－way road in the city［D］．Changsha:Changsha University of Science＆ Technology，2005．

［8］史 峰，黄恩厚，等．城市微循环交通网络中单行交通组织优化［J］．交通运输系统工程与信息，2009，9(4):30－35．SHI Feng，HUANG En-hou，et al．Optimization of one －way traffic organization of urban micro－circulation transportation network［J］．Journal of Transportation Systems Engineering and Information Technology，2009，9(4):30－35．

［9］Shi F，Huang E H，et al．Bi－ level programming model for reconstruction of urban branch road network［J］．Journal of Central South University of Technology，2009，16(1):172－176．

［10］Long D F，Shi F，Wang Y Z．One－way traffic organization based on traffic load and road equity［J］．Journal of Transportation Systems Engineering and Information Technology，2010，(6):109 －114．

［11］Wang Y Z，Long D F，Shi F．Cellular automation model for analyzing capacity of branch road section［J］．Journal of Central South University of Technology，2011，(5):1744－1749．