瞬变电磁法三分量联合处理与解释
2012-01-04谭劭聪席振铢
谭劭聪,王 鹤,席振铢,周 胜
(1. 中南大学 有色金属成矿预测教育部重点实验室,长沙 410083;2. 中南大学 地球科学与信息物理学院,长沙 410083;3. 长沙五维地科勘察技术有限责任公司,长沙 410205)
瞬变电磁法(Transient electromagnetic method,TEM)属于时间域电磁法,是利用阶跃波形电磁脉冲激发,通过不接地回线框磁性源和接地有限长导线电性源向地下发射一次场,在一次场的间歇期间测量地下介质产生的感应二次场的一种地球物理勘探方法[1−2]。在过去的几十年里,人们对瞬变电磁法的研究大多是计算出电磁场相关量,其中KREZIS等推导出导电半空间里瞬变电磁场三分量的具体表达式[3−7]。而对资料的解释还主要停留在单一分量上(以垂直分量为主)[8],已远不能满足目前的生产和勘探需要,同时也造成巨大的信息浪费。因此,联合水平分量,对三分量进行综合处理与解释,进一步提高解释精度,在理论和应用方面均有重要意义。本文作者用板状体作为野外地电模型,通过计算本征电流产生的电磁响应,对板状体产生的磁场三分量进行联合处理与解释,并通过物理模拟实验进行验证。
1 计算与分析
1.1 计算
在解决导电薄板瞬变电磁响应问题时,常用的数值解法是运用“等效模型”进行计算。而本文作者将用相对较简单的“本征电流模型”进行计算解释。Gallagher曾在不考虑本征电流间互感的前提下,用15个本征电流环来模拟薄板导体的电磁响应[9]。在早期,15个本征电流皆会产生瞬变电磁响应,即

而在晚期,瞬变电磁响应只由最里层的本征电流环引起,即

而对于无散电流场而言,本征电流的响应亦可用Galerkin方法表示出来:

由于不考虑本征电流间的互感,故异常可简单看做15个本征电流环响应的叠加,即

亦即

式中:Sxi、Syi、Szi是与第i个本征电位有关的二次场3个分量的分布系数,即二次场系数。Di(t)是第i个本征电流的电性系数,它与观测时间、板的大小和电导率值有关;Hxi、Hyi、Hzi分别是第i个本征电流在直角坐标系下 x、y、z方向上的激励系数,可通过计算每个本征电流和发送电流之间的耦合系数得出。为了通过几个分量的相互比值获得能揭示板状体与地面倾角关系的函数,将每两个分量为一组,通过排列组合综合比较计算 Hz/Hx、Hz/Hy、Hx/Hz、Hx/Hy、Hy/Hx和Hy/Hz。研究发明,由于z分量异常响应最强,x分量次之,则 Hz/Hx计算所得出的图形最为规律,直观。配合y分量响应值判断地面倾角关系,可为进一步的分析解释提供依据[10−12]。设函数如下:

1.2 数值模拟及结果分析
设发送矩形回线天线规格为10 m×10 m 40匝,接收矩形回线天线规格为5 m×10 m 40匝(通过调整天线放置方式达到测量3个方向分量的目的,其中x分量与测线方向平行,y分量与测线方向垂直,z方向与测线方向垂直且垂直于地面),分别在发送天线前方设置低阻板状体(规格为40 m×40 m×0.5 m,距离地面 10 m,与地面倾角分别为 0°、45°、90°和 135°),测线以 2 m为间距设置 51个点(测线设置如图 1所示)[13−14],再设均匀半空间电阻率为1 000 Ω·m,并用EMIT公司的Maxwell软件进行数值模拟[15],测量其响应特征,绘制其响应曲线。

图1 测线装置示意图Fig. 1 Measuring instrument and survey line图 2 倾角为 0°时板状体三分量响应及线圈与板状体倾角关系图Fig. 2 Abnormalies of three components of plane at tiltedangle of 0° and arrangement of loop and plane
从模拟结果来看,当板状体倾角为0°时,可知x分量为双峰异常,过零点为板状体中心且过零点在相同距离内响应的绝对值相等,z分量在板状体内部响应最强,以板状体中心为对称,y分量数值上极小。而P(r, t)函数图像为双曲线,可看到当板状体倾角为0°时,两边尖角对应点号分别靠近板状体边缘,中间值分别为无穷大和无穷小,所对应点号刚好为板状体的中心。

图1 测线装置示意图Fig. 1 Measuring instrument and survey line图 2 倾角为 0°时板状体三分量响应及线圈与板状体倾角关系图Fig. 2 Abnormalies of three components of plane at tiltedangle of 0° and arrangement of loop and plane

图3 倾角为0°时P(r, t)函数图Fig. 3 Distribution of function P(r, t) at tilted-angle of 0°
当板状体倾角为45°时,x分量和z分量皆为单峰异常,且板状体内部z分量异常比x分量强,y分量异常极弱,而P(r, t)函数图像上双峰间过零点为板状体靠近天线的边缘,整体图像向左偏移,亦可说明板状体位置较地面左倾,即与地面倾角为45°。

图4 倾角为45°时板状体三分量响应及线圈与板状体倾角关系图Fig. 4 Abnormalies of three components of plane at tiltedangle of 45° and arrangement of loop and plane
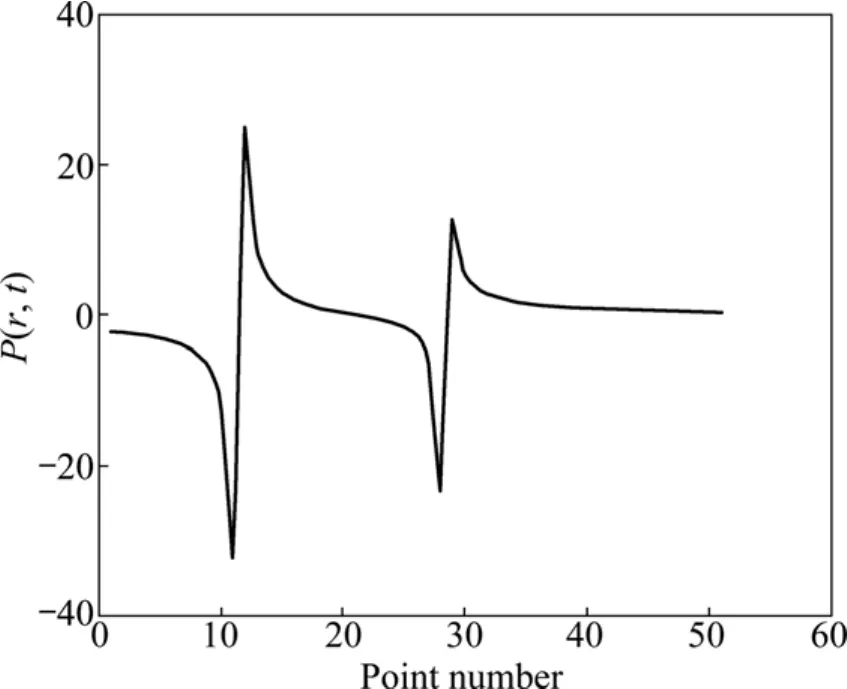
图5 倾角为45°时P(r, t)函数图Fig. 5 Distribution of function P(r, t) at tilted-angle of 45°
当板状体倾角为90°时,x分量为双峰异常,以过零点呈中心对称。z分量也为双峰异常,但以过零点呈轴对称。y分量异常极弱,而P(r, t)函数图像上无穷趋于零的点为板状体所在位置,两侧双峰以此呈中心对称。
当板状体倾角为135°时,x分量和z分量皆为单峰异常,且板状体内部z分量异常比x分量强,y分量异常极弱,而P(r, t)函数图像上过零点为板状体靠近天线的边缘,整体图像向右偏移,亦可说明板状体位置较地面右倾,与地面倾角为135°。

图6 倾角为90°时板状体三分量响应及线圈与板状体倾角关系图Fig. 6 Abnormalies of three components of plane at tiltedangle of 90° and arrangement of loop and plane

图7 倾角为90°时P(r, t)函数图Fig. 7 Distribution of function P(r, t) at tilted-angle of 90°
2 物理模拟与验证
实验采用的仪器是白云仪器公司生产的瞬变电磁仪MSD-1,采用矩形回线装置,其中发送回线规格为10 cm×10 cm 40匝,接收回线规格为5 cm×10 cm 40匝,发送电源为12 V,频率为25 Hz,叠加50次,采用40个时窗进行采样,并在发送天线前方设置低阻板状体(规格为40 cm×40 cm×0.5 cm,与发送回线夹角分别为0°和90°),测线以5 cm为间距布置21个点,进行两组实验,通过调整接收天线放置方式达到测量三分量的目的,实验结果如下(为第1、10、20、30道响应曲线,其中曲线上的数字表示采样时间道)。

图 8 倾角为 135°时板状体三分量响应及线圈与板状体倾角关系图Fig. 8 Abnormalies of three components of plane at tiltedangle of 135° and arrangement of loop and plane

图9 倾角为135°时P(r, t)函数图Fig. 9 Distribution of function P(r, t) at tilted-angle of 135°
物理模拟结果与数学计算模拟所得结果非常吻合,其中中间过零点为板状体的中心,过零点两旁为趋向于无穷的点,两边出现尖角处所对应点靠近板状体的边缘,即使减小测点数量仍能准确判断。
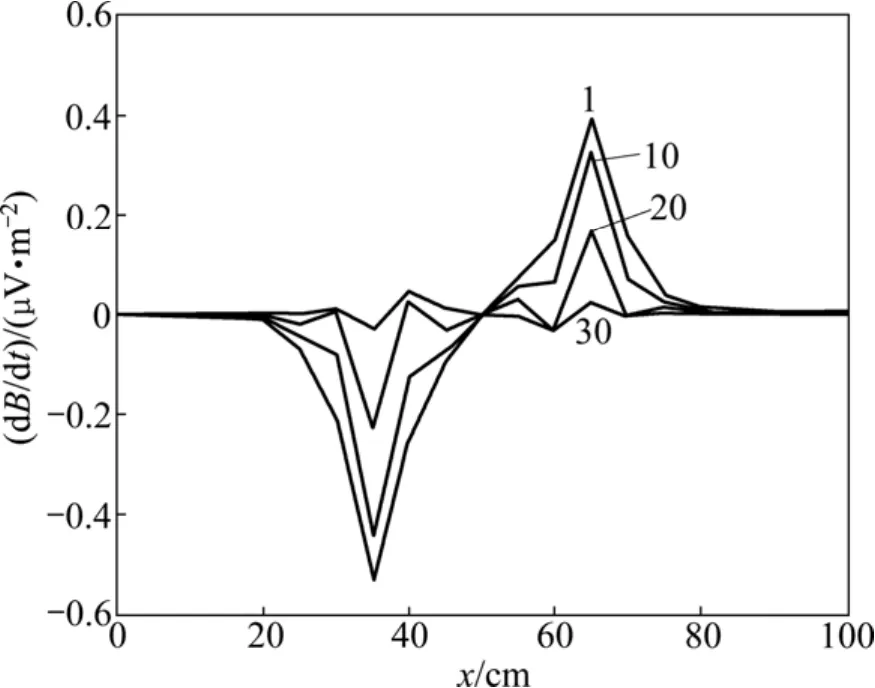
图10 夹角为0°时x分量响应图Fig. 10 Anormaly of x component at tilted-angle of 0°

图11 夹角为0°时z分量响应图Fig. 11 Anormaly of z component at tilted-angle of 0°

图12夹角为0°时P(r, t)函数图Fig. 12 Distribution of function P(r, t) at tilted-angle of 0°

图13 夹角为90°时x分量响应图Fig. 13 Anormaly of x component at tilted-angle of 90°

图14 夹角为90°时z分量响应图Fig. 14 Anormaly of z component at tilted-angle of 90°
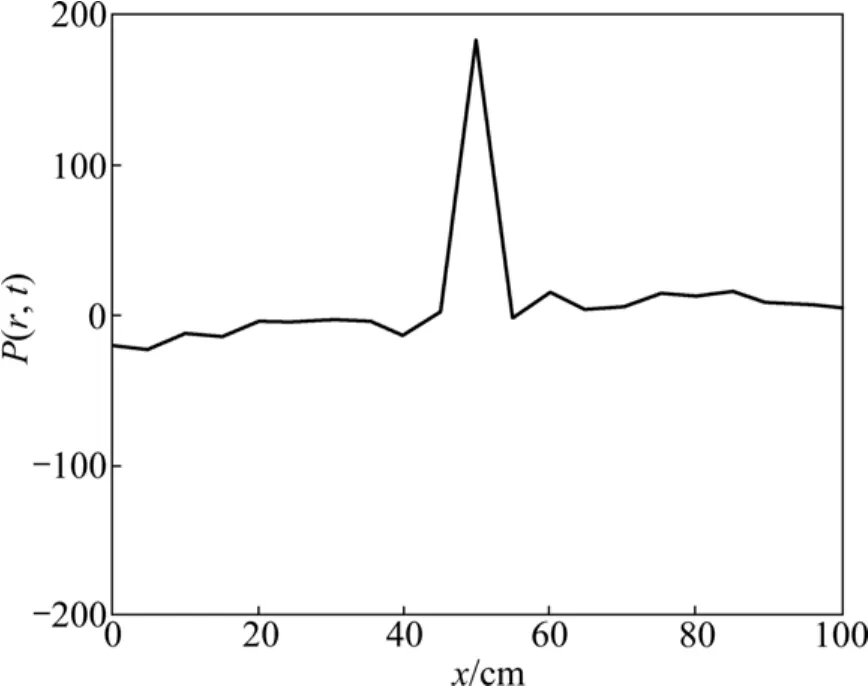
图15夹角为90°时P(r, t)函数图Fig. 15 Distribution of function P(r, t) at tilted-angle of 90°
当夹角为 90°时,物理模拟结果与数学计算模拟所得结果比较吻合,其中理论计算时中间应为无穷趋于零的点,但在实际测量时x分量仍能测量到极小响应,故中间相当于扩大几十倍并趋于正无穷,但并不影响判断板状体所在位置,原来过零点为垂直板状体所在位置,在实际应用时则为趋于无穷大单峰处。而峰的两侧分别有相反方向的两个尖角,仍与理论计算所得结果比较吻合。
3 结论
1) 当P(r, t)函数图像为双曲线时,板状体与地面平行,曲线上尖头为板状体的两边缘,而中间趋于无穷所对应点为板状体中心。
2) 当P(r, t)函数图像为双峰曲线时,板状体与地面垂直,中间无穷趋于零所对应的点为板状体所在的位置。
3) 当P(r, t)函数图像为多峰曲线时,可根据曲线整体偏移方向判断板状体与地面倾角大致范围,且最大峰值(或最小峰值)与相邻极小值(或极大值)间的过零点为板状体靠近线圈的一端。
4) 在数值模拟实验中,所处地层为平整地层,y分量总体异常响应都偏小,即说明地层走向基本稳定,也符合异常规律。
[1] 牛之琏. 时间域电磁法原理[M]. 长沙: 中南大学出版社,2007: 1−6.NIU Zhi-lian. Theory of time domain electricmagnetic method[M]. Changsha: Central South University Press, 2007: 1−6.
[2] 李 貅. 瞬变电磁测深的理论与应用[M]. 西安: 陕西科学技术出版社, 2002: 1−4.LI Xiu. The theory and application of transient electromagnetic sounding [M]. Xi’an: Shaanxi Science and Technology Press,2002: 1−4.
[3] TSAKNAKIS H J, KRIEZIS E E. Transient electromagnetic fields due to a circular current loop perpendicular or parallel to a conducting half-space [J]. IEEE Trans Geosci Remote Sens,1982, 20(1): 122−130.
[4] THEODOULIDIS T. Analytical model for tilted coils in eddy-current nondestructive inspection [J]. IEEE Trans Magn,2005, 41(9): 2447−2454.
[5] TSAKNAKIS H J, KRIEZIS E E. Field distribution due to a circular current loop placed in an arbitrary position above a conducting plate [J]. IEEE Trans Geosci Remote Sens, 1985,23(6): 834−840.
[6] SADEGHI S H H, SALEMI A H. Electromagnetic field distributions around conducting slabs, produced by eddy-current probes with arbitrary shape current-carrying excitation loops [J].IEE Proc Sci Meas Technol, 2001, 148(4): 187−192.
[7] JUILLARD J, DE BARMON B, BERTHIAU G. Simple analytical three-dimensional eddy-current model [J]. IEEE Trans Magn, 2000, 36(1): 258−266.
[8] 韩自豪. 磁性源瞬变电磁场水平分量响应特征与应用[D]. 北京: 中国地质大学(北京), 2009: 17−33.
HAN Zi-hao. Horizontal components response and its application of magnetic sources transient electromagnetic method [D]. Beijing: China University of Geoscience (Beijing),2009: 17−33.
[9] 刘 剑. 瞬变电磁法三分量测量研究[D]. 长沙: 中南大学,2009: 18−23.
LIU Jian. Three-component measurement in transient electromagnetic method [D]. Changsha: Central South University, 2009: 18−23.
[10] 刘金涛, 顾汉明, 胡祥云. 瞬变电磁法三分量解释剖析[J]. 人民长江, 2008, 39(11): l14−l16.
LIU Jin-tao, GU Han-ming, HU Xiang-yun. Analysis of three-component transient electromagnetic [J]. Yangtze River,2008, 39(11): 114−116.
[11] 戚志鹏. 瞬变电磁多分量解释技术研究[D]. 西安: 长安大学,2009: 38−43.
QI Zhi-peng. The multi-component interpretation technology of transient electromagnetic method [D]. Xi’an: Chang’an University, 2009: 38−43.
[12] MCNEILL J D. Why should I measure three components in a time—domain electromagnetic survey [R]. Mississauga: Geonics Limited, 1992.
[13] CHEN C S, CHIU W H, LIN C R. Three component time—domain electromagnetic surveying: Modeling and data analysis [J]. Piers Online, 2008, 4(4): 475−480.
[14] ZONGE K L, CARLSON N R. The utility of horizontal component measurements in random—walk TEM surveys [R].Tucson: Zonge Engineering & Research Organization Inc, 2002.
[15] 熊 斌. 瞬变电磁法三分量正演[EB/OL]. 2011−08−22.http://www.paper.edu.cn/.
XIONG Bin. Three-component forward of TEM [EB/OL].2011−08−22. http://www.paper.edu.cn/.
