一种具有自定义功能的管网系统性能仿真平台初探

李林磊， 林 峰

（ 1.中国科学院工程热物理研究所，北京 100190；2.中国科学院研究生院，北京 100190）

一种具有自定义功能的管网系统性能仿真平台初探

李林磊1，2， 林 峰2

（ 1.中国科学院工程热物理研究所，北京 100190；2.中国科学院研究生院，北京 100190）

管网系统在能源、化工、冶金等行业都有着广泛的应用，而其性能仿真研究却面临着通用性和专业性矛盾的问题，因此，文章提出了以Matlab/Simulink工具为平台来解决矛盾的思路。借助于Matlab/Simulink可以自定义能够满足特殊需求的专业元器件模型库，并搭建不同的系统模型，最后再借助于循环求解器进行求解。作为这种思路的初步探索，文章首先设计了两类单管路仿真模型，介绍了串、并、混联管路仿真模型的搭建方法，选取了文献中的两个复杂管网系统作为算例，对其进行了建模与求解，结果证明采用该思路进行管网系统性能仿真研究的可行性与正确性。该研究为今后建立具有通用性和灵活性、并同时能适应各种专业特殊需求的自定义功能的仿真平台打下基础。

管网系统；自定义；仿真平台

0 引言

管网系统广泛应用于国民经济各个领域，如城市给水、天然气石油供给、大型化工装置、风机空调流体系统和太阳能热发电系统等。由于这些管网系统一般具有投资成本高且偿还周期长的特点，因此，对其性能进行研究，在节约投资、避免造成工程浪费方面具有重要意义。然而管网系统结构复杂，布置型式多样，用户需求多变，因此，实现对管网系统的性能分析，就要求仿真平台不仅具备通用性、灵活性，而且还要拥有各种能模拟不同专业元器件的模型库。

目前的管网系统性能仿真平台主要分为两大类：商用性能仿真平台和专用性能仿真平台。商用性能仿真平台通常是采用标准高级程序设计语言（如FORTRAN、C、C++语言）编写，如孟山都公司的FlowTran系统、ASPEN公司的ASPENPLUS系统、美国科学模拟公司的PROCESS系统和Coade公司的MicroCHESS系统等[1]。它们一般具有较好的通用性和灵活性，可广泛应用于各种模拟系统；但由于缺乏专业元器件库 （比如压气机、风机的特性线模型以及专业的阀门等）或无法求解特殊动态方程而不能满足需求；专用性能仿真平台虽能满足专业的特殊需求，但由于其针对特定对象而专门开发，因此缺乏通用性和灵活性。

为解决管网系统性能仿真研究目前所面临的这一两难问题，本文提出了以Matlab/Simulink工具为平台来解决这个矛盾的思路，并进行了初步探索。首先，由于Matlab/Simulink拥有各种能实现不同功能的基础模块库，因此，用户可以根据自己的需要自定义不同的元器件模型，然后再根据实际的串并联关系灵活搭建不同的系统模型，最后借助于循环求解器进行自动求解[2]。

为验证采用上述思路进行管网系统性能仿真研究的可行性与正确性，本文以Matlab/Simulink工具为平台，首先自定义了两类单管路模型，然后介绍串、并、混联管路模型的搭建方法。最后以两个具体管网系统作为实例，对其进行建模与求解。

1 单管路模型

式中hf、hij——管道压头损失/m；

f——沿程阻力系数；

l——管道长度/m；

d——管道直径/m；

V——流体在管道内的流速/（m/s）；

g——重力加速度/（m/s2）；

qij——各管道体积流量/（m3/s）。由于管网系统的水力分析通常围绕求解管路压降和流量进行，因此，本文首先自定义了两类单管路模型，分别用于求解管路压降和流量。

1.1 第一类单管路模型 （求压降）

式中Re——雷诺数；

ε——管道粗糙度/m；

v——流体运动黏性系数/（m2/s）；

Q——管路体积流量/（m3/s）；

A——管道截面积/m2。

因此，第一类单管路模型是已知l、d、ε、v和Q，求解hf，根据式 （1）搭建该管路仿真模型如图1所示。

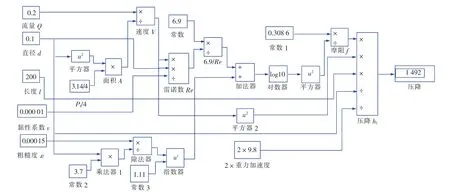
图1 第一类单管路模型

从图1可以看出，仿真模型是由各代表一定物理意义的不同模块连接而成，用户只需要输入l、d、ε、v以及Q，系统即可自动算出hf。为了更加突出水力分析所关注的物理量，同时使用户界面更加美观，可以对图1所示管路模型进行简单封装，封装后的模型如图2所示。当用户双击该子系统模块 “Subsystem”时，同样可以进行参数的设置。

图2 封装后第一类单管路模型

1.2 第二类单管路模型 （求流量）

第二类单管路模型是给定压降求流量。与传统的求解思路不同，本文并不需要由hf求解出Q的表达式，而是通过求解关于Q的代数方程 （代数环）得到Q的值。

关于此类复杂非线性代数方程 f（z）=0的求解，Simulink循环求解器采用的是Newton法 （牛顿法）。该方法的收敛性依赖于初始值的选取，若初始值偏离所求根较远，则可能导致发散。因此，为保证代数环收敛，需要给代数状态z赋予一个较好的初始状态值。采用Math Operation库中的Algebraic Constraint（代数约束）模块可以很方便地建立代数环模型，并在模块对话框内指定初始状态的估计值，该模块强制输入信号f（z）为零，并输出一个代数状态z。由于这个模块的输出必须经过反馈回路影响输入，因此，模块会调整其输出使其输入为零[5]。

图3 第二类单管路模型

第二类单管路模型是已知 l、d、ε、v和 hf，求解Q，求解过程是根据f（z）=0建立一代数环，设定初始状态估计值为0，经多次迭代求出Q值。搭建该管路仿真模型见图3，封装后模型见图4。

图4 封装后第二类单管路模型

2 管路简单连接模型

实际管网布置型式通常可分为串、并、混联三种，如何根据本文设计的两类单管路模型实现这些简单的连接，下面将一一介绍。

2.1 串联管路模型

图5为三管路串联示意，已知流量Q，求管路总压降hf。

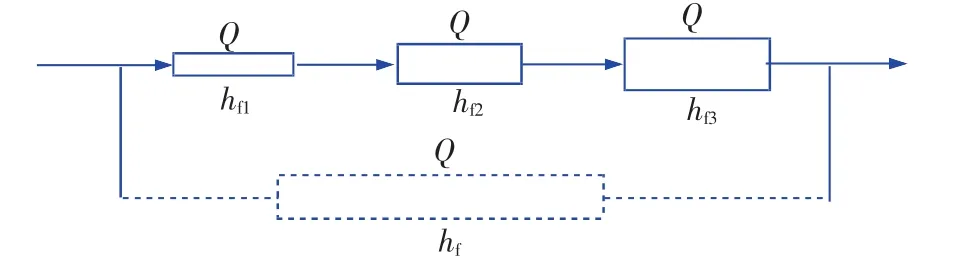
图5 串联管路示意

如图5所示，流经各管路流量为Q，各管路压降分别为hf1，hf2，hf3，选择第一类单管路模型搭建该串联管路仿真模型，如图6所示。系统输入为流量Q，输出为各管路压降之和hf=hf1+hf2+hf3。

图6 串联管路仿真模型

2.2 并联管路模型

图7为三管路并联示意，已知管路压降hf，求流经各管路流量Q1，Q2，Q3和该并联管路总流量Q。

图7 并联管路示意

如图7所示，各并联管路压降为hf，流量分别为Q1，Q2，Q3，选择第二类单管路模型搭建该并联管路仿真模型，如图8所示。系统输入为压降hf，输出为各管路流量Q1，Q2，Q3和总流量Q=Q1+Q2+Q3。

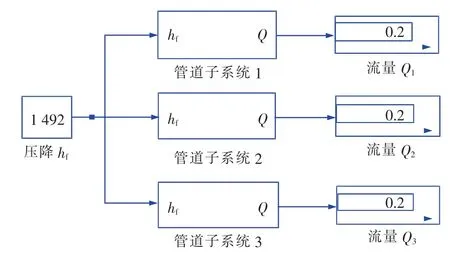
图8 并联管路仿真模型示意

2.3 混联管路模型

图9为三管路混联示意，已知管路进口总流量Q，求管路总压降hf和管路2、3的流量Q2、Q3。

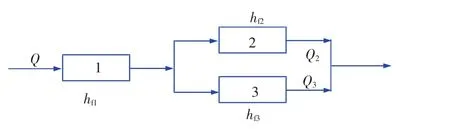
图9 混联管路示意

图9中，管路2、3并联后与管路1串联。因此，对于管路1，选择第一类单管路模型，输入流量Q，输出压降hf1；对于管路2、3，选择第二类单管路模型，根据并联管路流量守恒Q=Q2+Q3和压降守恒hf2=hf3可建立一代数环模型，模型输出为hf2，初始状态估计值设定为300，搭建系统仿真模型如图10所示。系统输入为流量Q，输出为Q2、 Q3和总压降 hf。

3 复杂管网系统性能仿真实例

为验证采用本文思路对复杂管网系统进行性能仿真的可行性，本文选取了两个管网系统水力分析实例，对其进行建模与求解。

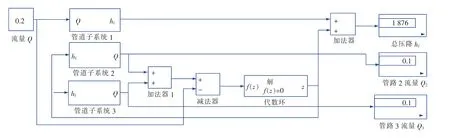
图10 混联管路仿真模型示意

3.1 管网系统仿真实例一

以文献 [6]中的管网系统为例 （图11），对其进行稳态仿真。已知该管网系统的进口流量Qin=8.50×10-2m3/s， 出口流量Qout1=2.83×10-2m3/s、Qout2=5.67×10-2m3/s，求各管路流量Q1～Q7。

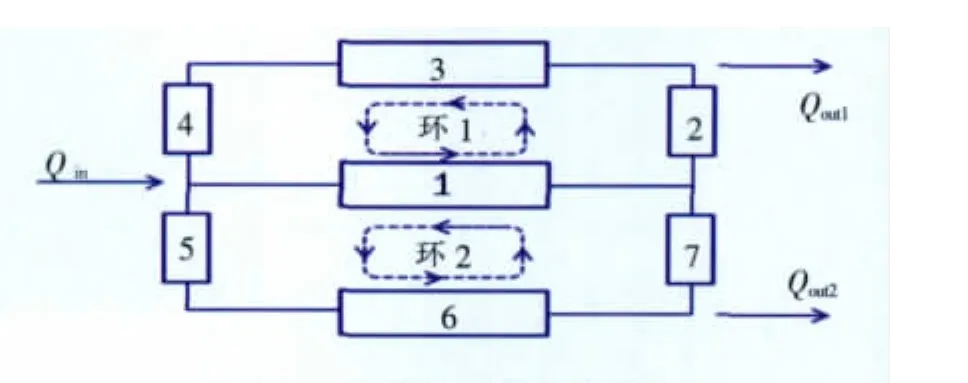
图11 实例一管路示意[6]

文献 [6]中实例的压头损失方程采用修正后的Darcy-Weisbach公式，即Hazen-Williams公式hf=KQn（其中）进行计算。为方便起见，现将原文该实例已知条件列于表1。

表1 实例一已知参数值[6]

由图11可得到各管路实际串并联关系如图12所示。

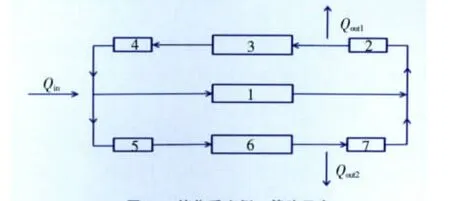
图12 简化后实例一管路示意

图13 实例一仿真模型示意

从图12可以看出，管路2、3、4和5、6、7分别串联后与管路1并联。根据流量守恒，流经管路2的流体一部分流向管路3、4，一部分流出管网，因此有Q3=Q4=Q2-Qout1；流经管路5和6的流体一部分流向管路7，一部分流出管网，因此有Q5=Q6=Q7+Qout2；而由进口节点处流量守恒可以得到Q4与Q5之间的关系为Q5=Qin+Q4-Q1，因此，管路2、3、4、5、6、7均选用第一类单管路模型，分别由流量求压降。根据并联管路压降守恒得到 hf1=hf2+hf3+hf4， hf2+hf3+hf4=hf5+hf6+hf7，因此，管路1选择第二类单管路模型，由压降hf1求流量 Q1； 由 hf2+hf3+hf4-（hf5+hf6+hf7） =0 可建立一代数环模型，模型输出为流量Q2。依据上述思路搭建系统仿真模型，如图13所示。

借助Algebraic Constraint（代数约束）模块，设定代数状态Q2的初始估计值为0，系统采用Newton法进行循环迭代，最终得到各管路流量，如表2所示。

表2 实例一稳态仿真结果

计算结果中负值表示管路流体实际流向与假设相反。对比发现，本文计算结果与文献 [6]基本一致，误差仅在1%以内。该误差主要来源于计算方法的不同：文献 [6]采用Hardy Cross法 （平差法）求解环方程，其基本思路是先给各管路分配一初始流量，求出各管路压降，若每环各管路压降之和不为零，则再对各管路引入校正流量，重复计算直到各环闭合差接近零为止；而本文则是以Matlab/Simulink工具为平台，直接根据实际管网串并联关系搭建仿真模型，借助代数环采用Newton法迭代求解。

3.2 管网系统仿真实例二

实例二以文献 [7]中管网系统为例 （图14），对其进行建模与求解。已知该管网系统进口压力Pi=550 kPa、Pl=900 kPa， 出口压力 Pj=250 kPa、Pk=200 kPa，求各管路流量Q1～Q8。

图14 实例二管路示意[7]

文献 [7]中该实例的压头损失方程采用下式：

式中G——管路通流能力，只与管路尺寸和流体物性有关；

ΔP——流体通过管路的压降/kPa；

F——管路流体的摩尔流量/（mol/h）。

为方便起见，现将原文各管路通流能力G列于表3。

表3 实例二各管路通流能力[7]

分析图14，各管路实际串并联关系如图15所示。

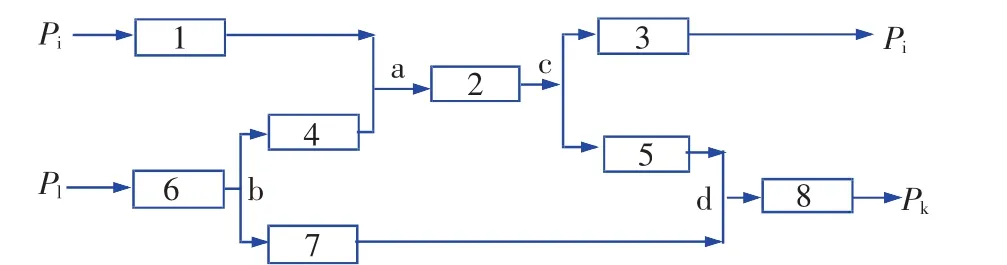
图15 简化后实例二管路示意

分析图15，管路1、2、3、6、7、8均选择第一类单管路模型，管路4、5选择第二类单管路模型。由各节点处流量守恒可以得到： （a）：Q2=Q1+Q4； （b）：Q7=Q6-Q4； （c）：Q3=Q2-Q5；（d）： Q8=Q5+Q7； 由压降守恒得到： （e）： Pi-Pj=P1+P2+P3； （f）： Pl-Pk=P6+P7+P8； （g）： Pi-Pk=P1+P2+P5+P8； （h）： Pl-Pj=P6+P4+P2+P3，将上述4个压降方程等号左右两侧相减即可建立4个代数环模型，模型输出分别设为Q1，P4，P5，Q6，据此搭建该系统稳态仿真模型，见图16。

借助Algebraic Constraint（代数约束）模块，设定代数状态Q1、P4、P5、Q6的初始估计值分别为10，400，400，10，系统经过循环迭代，最终得到各管路流量见表4。

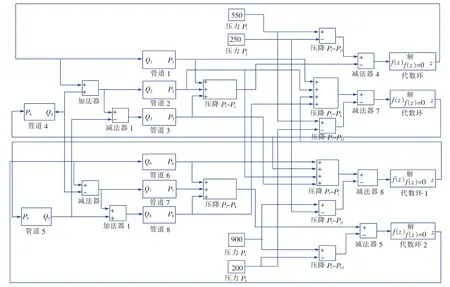
图16 实例二稳态仿真模型示意

表4 实例二稳态仿真结果

该计算结果与文献 [7]完全一致。由于该稳态仿真模型的建立本质上也是依据压头损失方程、流量守恒方程和压降守恒方程，因此，本文的仿真结果与文献 [7]完全一致并非偶然。

4 结论

（1）本文以Matlab/Simulink工具为平台，通过自定义专业元器件模型库为管网系统性能仿真研究所面临的通用性和专业性之间的矛盾提出了一种解决思路，并通过实例证明了这个思路的可行性与正确性。

（2）本文以Matlab/Simulink工具为平台，自定义了两类单管路模型，并介绍了串、并、混联管路模型的搭建方法，最后通过实例证明了采用该思路进行管网系统性能仿真研究的可行性。

（3）本文研究思路的实现为今后建立具有通用性和灵活性，并同时能适应各种专业特殊需求的自定义功能的仿真平台打下基础。

[1]丁军平.复杂给水管网的流量计算与分析[D].西安科技大学，2006.

[2]宋海华，余国琮，王秀英.精馏过程的动态模拟[J].化工学报，1994，45（4）∶413-421.

[3]李鸣.管网基本定理及其数学模型[J].节水灌溉，2001，（1）∶1-2.

[4]吕谋，李红卫.给水管网平差计算中各种流量法的分析和比较[J].青岛建筑工程学院学报，1993，15（4）∶1-2.

[5]李颖.Simulink动态系统建模与仿真[M].西安：西安电子科技大学出版社，2009.

[6]HODGE B K，ROBERT P TAYLOR.ANALYSIS AND DESIGN OF ENERGY SYSTEMS[M].USA∶Rhodora Penaranda，1998.

[7]马继勇.管网系统通用动态模拟算法及应用[D].北京化工大学，2008.

Study on Pipenet System Performance Simulation Platform with Custom Function

LI Lin-lei（Institute of Engineering Thermophysics， Chinese Academy of Sciences， Beijing 100190，China）,LIN Feng

Pipenet system has a wide range of applications in energy， chemical， metallurgical and other industries,but its performance simulation study is facing with a dilemma about the versatility and professionality.Therefore,this paper presents a new idea to resolve this conflict by taking the Matlab/Simulink as a tool,and conducts a preliminary exploration.The professional component model library can be customized to meet the special needs by means of Matlab/Simulink,and different system models can be built and finally solved with loop solver.As a preliminary exploration of this idea,this paper designs two single-line simulation models and introduces the method to build series,parallel and series-parallel simulation models first.Then,two complex pipenet systems are selected from other papers to be modeled and simulated as the computation examples.Results show the feasibility and correctness of the idea,and lay the foundation for the future simulation platform,which should have the features of versatility and flexibility as well as the custom function being adapted to the special professional needs.

pipenet;custom;simulation platform

10.3969/j.issn.1001-2206.2012.05.001

李林磊 （1987-），女，湖北黄冈人，中国科学院工程热物理研究所硕士研究生，主要研究领域为管网系统模拟与仿真研究。

2011-12-25；

2012-05-30