灰色关联模型在投标前期决策中的应用*——基于层次-熵值组合赋权的研究

崔东红，尚思彤

（沈阳工业大学管理学院，沈阳 110870）

灰色关联模型在投标前期决策中的应用*
——基于层次-熵值组合赋权的研究

崔东红，尚思彤

（沈阳工业大学管理学院，沈阳 110870）

面对建设市场上的多个项目，承包商采用科学、合理、易于实施的投标决策方法是建设承包市场的现实要求。基于此，介绍改进的层次分析法、熵值法、灰色关联原理及其在建设工程项目投标决策中的运用。根据工程实际，建立投标前期决策指标体系，并用层次-熵值组合赋权法确定权重，在此基础上利用改进后的灰色关联分析模型对多个项目进行评价，并通过工程算例验证该方法，证明其能够很好地克服单一方法的局限性，选择出最优的项目，使投标决策更加公正、科学。

建设承包;投标决策;层次分析法;熵值法;层次-熵值组合赋权法;灰色关联模型

随着市场经济体制的不断深入和招投标制度的大力推行，我国建设市场逐步走向规范和完善。面对建设市场上的多个拟投标项目，承包商能够采用科学、合理、易于实施的投标决策方法进行决策是建设承包市场的现实要求。然而在实践中，承包商在面对多个项目时，决策者往往“拍脑袋定项目”，见标就投，希望达到“东边不亮西边亮”的效果，赢得中标机会。这种“全面撒网，重点捕鱼”的策略，不但分散了投标工作的人力、物力、财力，而且提高了投标成本，降低了中标率，而且即使中标也难以盈利，造成大量资金和机会的浪费，影响到企业的生存和发展。因此，投标前加强分析，恰当地选择投标项目是投标制胜的前提。本文根据工程项目的特点，提出采用将项目的客观信息和决策者的主观意向相结合的层次-熵值组合赋权法确定权重，并利用灰色关联分析模型选出最有利的项目，从而提高投标前期决策方法的科学性、合理性。

一、投标前期决策指标体系构建

1.影响因素分析

面对多个工程项目，为了有选择地进行投标，承包商在进行决策之前必须进行企业内部情况和外部环境的调查分析，以便知己知彼、科学决策。企业自身情况的决策分析主要是综合考虑技术方面的实力、经济方面的实力、管理方面的实力、信誉方面的实力等，主要包括企业技术设备条件、人员条件、类似经验、资金条件、信誉与合作能力、竞争水平、应变能力、相关业绩及自身特殊优势等方面。企业外部环境分析主要包括业主环境、项目环境、竞争对手环境分析等。业主环境主要包括业主信誉、业主资金落实程度、业主招标条件及业主技术管理水平;项目环境主要包括项目规模、施工难度、经济价值、市场潜力、合同条件、施工技术难度、工程复杂程度、工期要求、工程风险等;竞争对手环境主要包括每个有可能成为竞争对手的企业的投标经历、竞争对手的实力和能力等。

虽然影响投标决策的因素很多，但并不是每项都是主要的因素，决策者要考虑到自身所能投入的时间和精力，选择那些有主要影响和代表性的因素作为评价指标，剔除不必要的因素。指标的选择也不是固定的，不同的承包商针对不同的项目所选择的因素可以是不同的。为了使投标决策的结果更为准确、科学，承包商应根据具体情况确定出既能概括决策范围、又便于独立对比分析的因素。

2.投标前期决策指标确定

国内学者一般将投标前期决策的影响因素归纳为以下11条［1－6］:

（1）管理条件。指承包方和业主是否都能抽出足够的、水平相应的管理和工程人员参加该工程，优化管理，降低成本，保证工程高效高质地完成。

（2）技术设备条件。指是否具备工程所需的各种技术要求，施工机械设备的品种、数量能否满足要求。

（3）项目施工难度。考虑项目工程质量、施工工艺、工期等方面的要求是否超出了本企业所掌握的施工技术范围。

（4）工程条件。包括地下构筑物、征地拆迁、水陆交通等情况。

（5）施工单位对同类型项目的承建经验。

（6）业主资金和信誉。主要指业主能否及时支付工程款及资金的落实程度等。信誉直接影响资金支付、工程进度，信誉不佳则有可能引起施工过程中的纠纷。

（7）承包方与业主关系。双方关系友好融洽，有利于工作中矛盾的解决，提高项目实施的效率。

（8）招标条件。应仔细分析招标文件，鉴别合同条款是否苛刻，以免增加合同风险和施工风险，无法满足业主要求。

（9）经济价值。指项目可能给承包商带来的预期收益及收益率。

（10）市场潜力。指该项目今后在该地区带来的影响和机会，对施工方市场声誉的影响以及未来发展的有利程度。

（11）项目的外部环境因素。包括投标竞争的激烈程度，所处位置是否便利，自然环境是否恶劣，市场经济状况是否有利（材料价格否稳定、相关政策影响）等。

本文参考已有的研究成果，结合施工企业内外部环境因素分析，舍去对决策影响较小的因素，同时为了便于分析和计算，将投标前期决策的影响因素分为项目因素、自身因素、业主因素、环境因素4类，每个因素下又分若干子因素，据此建立了投标前期决策评价指标体系，如图1所示。

二、评价方法

（一）权重的确定

对于任何多指标的综合评价模型，确定指标权重是模型中重要的一步，有时也是最困难的一步，指标权重不同有可能导致评价结果不同［7］。因此，应该以科学的方法得到最符合实际的权重。确定权重的方法分为主观型和客观型两大类:主观型是根据决策者对各项指标的主观判断来赋权，如Delphi法、层次分析法等;客观型是依据客观信息进行赋权，如熵值法、CRITIC法等。无论主观型还是客观型方法都存在一定的片面性，实际中往往主客观结合使用。

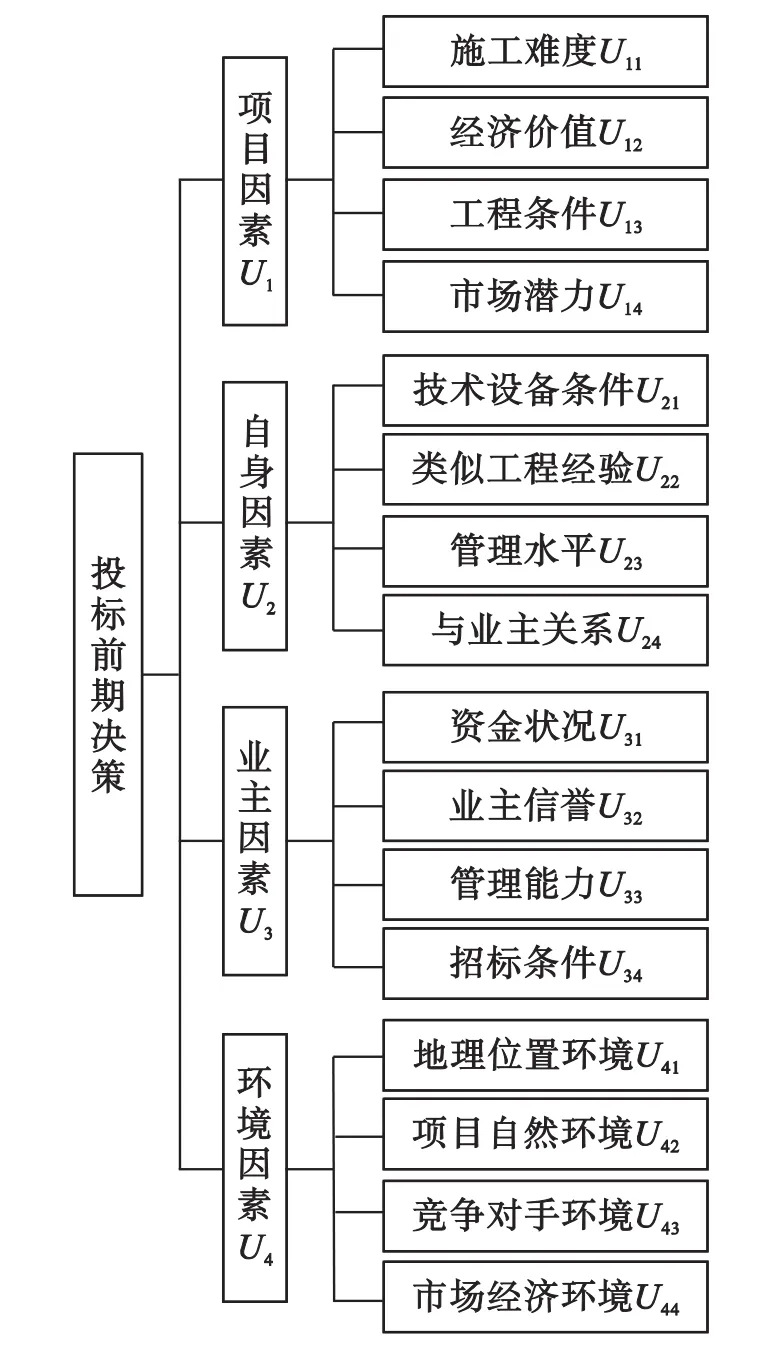
图1 投标前期决策评价指标体系

权重的构成是否合理，直接影响到评价体系的科学性。为克服评价过程中主观片面性和信息不对称的缺陷，本文结合主观赋权与客观赋权的优点，采用熵值法与层次分析法组合赋权来改进灰色关联分析模型，以此来评价投标项目的优劣。

1.改进的层次分析法（IAHP）

层次分析法的难点是建立正确的判断矩阵，而IAHP采用自动调节的方式建立比较矩阵，可自然满足一致性要求，直接求解可得各权重值［8］28。该方法克服了AHP法（1/9，9）标度重要性排序过程的不确定性以及权值计算和一致性检验的复杂性，具有直观、简捷的特点。IAHP法的应用步骤如下［9－11］:

（1）建立层次结构模型。把影响投标前期决策的指标按属性分组，形成不同层次，建立递阶层次结构，见图1。

（2）建立比较矩阵Aij。通过专家评分，对每组指标采用三标度法，两两比较其相对重要性，得出比较矩阵

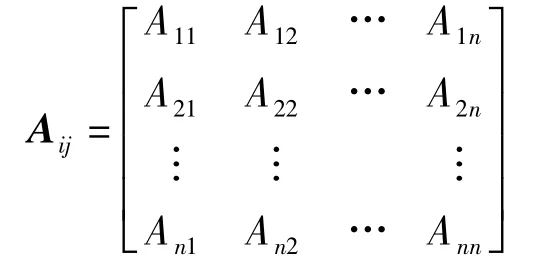
其中，Aij为第i指标和第j指标的相对重要性比值，且有Aii=1。

（3）计算重要性排序指数

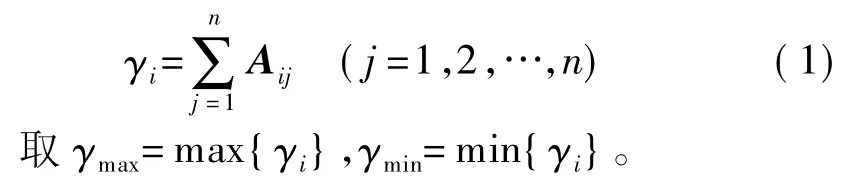
（4）构造判断矩阵

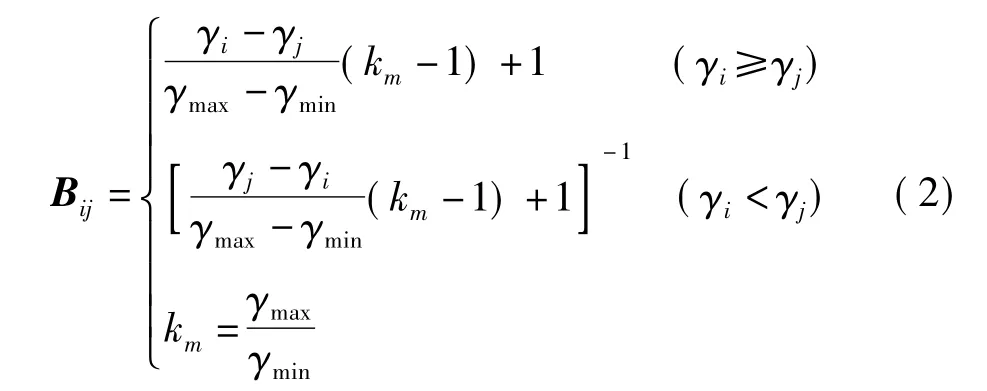
（5）求Bij的传递矩阵

（6）求Cij的最优传递矩阵

（7）求Bij的拟优一致矩阵

（9）利用单层次排序结果进行总层次排序，得到权重ωi。如果某一指标权重为a，其下因素的权重为，则在总排序中这些因素的权重为ωi=aWi，i=1，2，…，n。

2.熵值法

熵值是根据各指标所携带信息的多少来确定各指标权重的。当各评价对象的某项指标值相差较大时，熵值较小，说明该指标提供的有效信息量较大，其权重也较大;反之，若某项指标值相差较小，则其权重也较小。当某项指标值完全相同时，熵值达到最大，则该指标在评价中不起作用。利用这一原理计算各指标的权重，可以为多指标评价提供依据。

熵值法主要有以下3个步骤［4，12］:

（1）原始数据矩阵的标准化。设有n个拟投标项目，要考虑的评价指标有m个。对于第j个项目第i个因素的指标值用表示，设原始数据矩阵为，对其标准化后得Xij=（xij）mn。

对于极大值指标（越大越好）利用公式

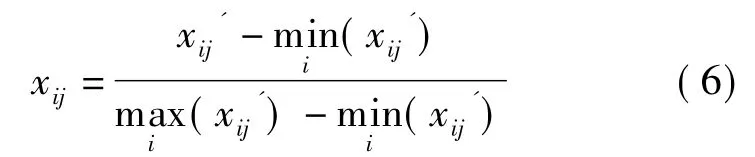
对于极小值指标（越小越好）利用公式

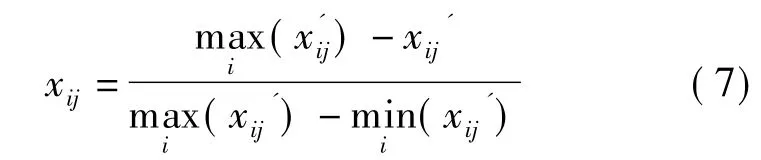
（2）定义熵值。第i个评价指标的熵定义为

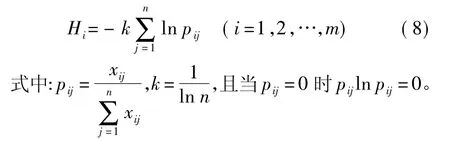
（3）定义熵权。第i个评价指标的熵权定义为

3.层次-熵值组合赋权法

改进的层次分析法可以在样本数据不多的情况下根据决策者的偏好和经验确定权重，具有可靠性高、灵活、简便等优点，但无法克服主观随意性较大的缺陷，当专家的判断与实际相差较大时，将导致错误的评价结果。而熵值法充分挖掘了原始数据蕴涵的信息，结果较为客观，但由于不能反映专家的知识和经验，有时得到的权重可能与实际重要程度不符，而且当样本数据较少时很难找到数据间的内在规律，此时熵值法所得权重不如主观赋权法。因此，在实际应用中结合层次分析法和熵值法是不错的选择［13］。

根据上述AHP计算求得的主观权重ωi和熵权理论求得的客观权重νi，将两者相结合得到综合权重

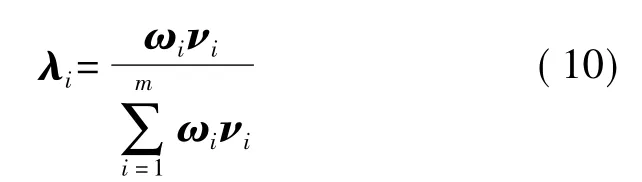
（二）改进的灰色关联模型

灰色关联分析是灰色系统理论中的重要组成部分，它是对运行机制与物理原型不清晰或者根本缺乏物理原型的灰关系序列化、模式化，进而建立灰关联分析模型，使灰关系量化、序化、显化，能为复杂系统的建模提供重要的技术分析手段［14］。其基本原理是通过对序列几何关系的比较来分清系统中多因素间的关联程度，序列曲线的几何形状越接近，则它们之间的关联度越大。基于以上理论及投标项目选择的特征，本文拟采用一种基于灰色关联分析的投标项目选择新方法。

改进的灰色关联模型在考虑主客观权重的基础上，根据评价对象建立比较序列，通过计算参考序列与各比较序列的关联度大小，判断该参考序列与比较序列的接近程度，从而评定各比较序列的等级。具体步骤是［15－16］:

（1）确定比较序列（评价对象）和参考序列（评价标准）。设评价指标为m个，拟评价项目为n个，采用专家评分法，构成序列，其中i=1，2，…，m;j=1，2，…，n。指标无量纲化处理可以直接利用熵值法中原始矩阵规范化后的结果。无量纲化后的序列构成比较序列Xj= （x1j，x2j，…，xij），i=1，2，…，m;j=1，2，…，n。

评价标准是各指标中的最优值，经过标准化处理的比较序列中各方案的最大值即是最佳方案参考序列，记为X0i=（x01，x02，…，x0i）T，i=1，2，…，m。

（2）计算灰色关联系数。根据灰色关联决策的理论，指标的关联系数为

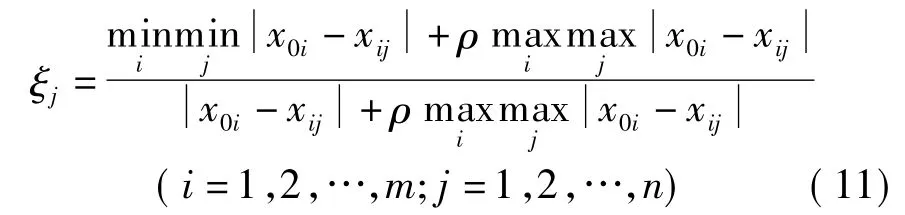
式中，ρ为分辨系数，ρ∈（0～1），通常取ρ=0.5。

（3）计算灰色关联度

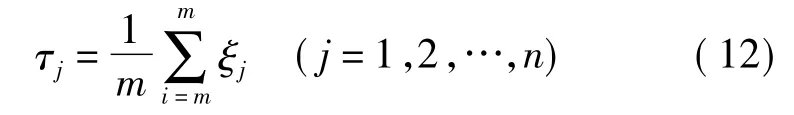
（4）计算灰色加权关联度。灰色关联分析法至少存在两点不足:权重的确定由于没有统一的方法而具有很大的主观性;“均一化”加权，没有体现因素间区别［17］。鉴于此，本文应用IAHP与熵值法相结合来改进灰色关联分析法，得到灰色加权关联度

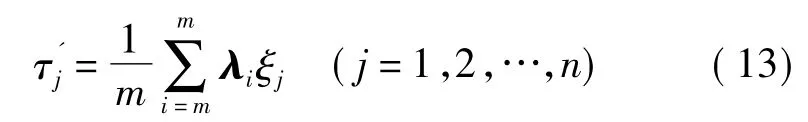
根据灰色加权关联度的大小，对各评价对象进行排序，关联度越大则评价结果越好、项目效益越好。

三、例证分析

某建筑工程企业获得了7个工程项目招标信息。经过内审，确定自身满足4个项目的要求，并准备参加2～3个项目进行投标。于是，该企业请来专家，对这4个项目进行综合评定，排出优劣，以确定投标项目。

（1）利用IAHP的三标度排序法构建评价指标的比较矩阵，进而得到指标的权重向量。以投标前期决策的4个指标项目因素、自身因素、业主因素和环境因素为例，比较矩阵为

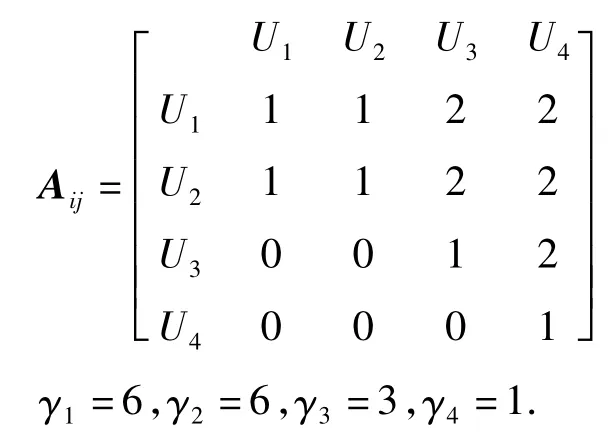
判断矩阵为

传递矩阵为

最优传递矩阵为

拟优一致矩阵为

同理，下层指标权重计算采用同样方法得出，即

由IAHP得出各指标的权重为

（2）利用熵值法进行客观赋权。由于投标影响因素的模糊性，专家不可能对各个因素精确评判，对于定性因素，根据优劣等级将其模糊定量化后相应评分。这里把每个因素分为5级，“好”为5分，“较好”为4分，“一般”为3分，“较差”为2分，“差”为1分。如果有定量因素，可直接计算或估算出具体值，从而得到原始指标数据矩阵，如表1所示。

表1 原始指标数据矩阵

在这些影响因素中，只有施工难度是极小值目标，其他为极大值目标，根据式（6）、（7）得到标准化矩阵，再根据式（8）得到熵值，即

根据式（9）得到熵权，即

（3）组合赋权。根据式（10）得到综合权重，即

（4）改进的灰色关联分析法排序。直接利用熵值法的标准化数据矩阵，可以得到参考序列为

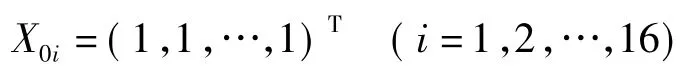
根据式（11）计算灰色关联系数矩阵为

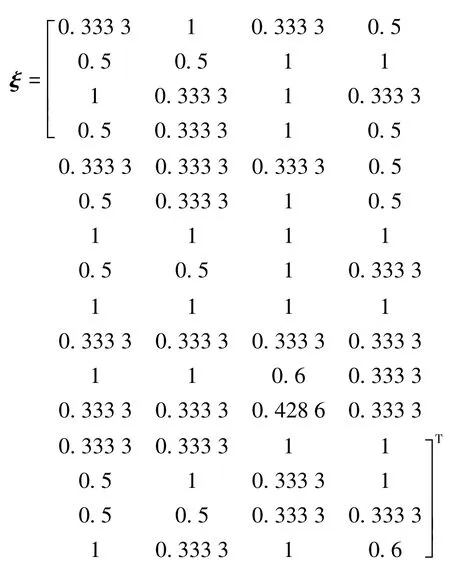
根据式（12）计算灰色关联度，得τ1=0.645 8，τ2=0.5937，τ3=0.704 2，τ4=0.564 3。即项目3＞项目1＞项目2＞项目4（“＞”表示“优于”）。在不考虑权重的情况下，可以选择项目1、2、3。根据式（13）计算灰色加权关联度，得=0.037 0，=0.029 9=0.049 2，=0.031 6。即项目3＞项目1＞项目4＞项目2。在考虑权重情况下，可以考虑选择项目1、3、4。

由此可以看出，承包商要把重点放在项目3的投标上，其次考虑项目1和项目4。项目2与参考项目相差较大，可以放弃。该方法考虑了客观权重和主观权重各自携带的不同信息，得到的综合权重既结合了专家的经验和偏好，又减少了主观随意性，因而更为合理;灰色关联分析的运用把不可确定的灰关系量化，能够快速、直观地得出每个项目与最优项目关联的大小，从而得出最适合承包商选择的项目。该方法克服了一般评价方法计算量大、流程复杂、难以理解的缺陷以及在权重确定上随意性大的不足，能够帮助改善长期以来依靠经验决策的局面，为投标方案评审提供一种量化分析的可行方法。

四、结束语

投标项目的选择需要综合考虑项目、技术、竞争对手等众多因素，这些因素既有已经被了解的白色信息，也有尚未被发现的黑色信息，而更多的是只能定性了解的灰色信息。灰色关联分析理论将复杂的指标评价经数学分析和计算转化为清晰直观的数值比较，使决策变得轻而易举，评价结果客观可信。本文以工程投标的影响因素为灰色关联决策的目标，并利用层次-熵值组合赋权法确定各评价指标的权重，建立了基于层次-熵值组合赋权的灰色关联多项目投标择优决策模型，结合了专家的经验判断和因素的客观信息，减少了人为的主观判断，具有较高的实用性，为承包商作出正确的决策提供了科学的依据。

［1］杨俊琴．投标决策支持系统研究［D］．重庆:重庆交通学院，2002:3－10．

［2］刘宏．基于人工神经元网络技术的投标前期决策研究［D］．重庆:重庆大学，2004:10－15．

［3］孟明星．建设工程投标决策模型研究与应用［D］．天津:天津大学，2006:8－12．

［4］徐靓，张九根，梁雪春．基于熵权决策法的建筑工程项目投标［J］．建筑经济，2006（3）:165－167．

［5］严薇，刘宏，刘亮晴．基于人工神经网络技术的投标前期决策［J］．重庆大学学报:自然科学版，2007，30（5）: 73－77．

［6］王守俊．建筑工程项目投标前期决策分析研究［D］．西安:西安建筑科技大学，2009:3－15．

［7］肖明，赵宏伟，王晓峰．用熵确定权重的方法研究［J］．商场现代化，2007（5）:21－22．

［8］张新玉．水利投资效益评价理论与方法［M］．北京:水利水电出版社，2005．

［9］杨传栋．层次分析中的三标度排序法［J］．曲阜师范大学学报，1994，24（2）:101－104．

［10］古小平，唐愉，张瑞，等．改进层次分析法在管道腐蚀评价中的应用［J］．石油化工腐蚀与防护，2007，24（2）: 52－53．

［11］陈杰，石超，方来华．基于灰色关联分析和IAHP的CNG加气站安全评价方法研究［J］．中国安全科学学报，2009，19（6）:159－165．

［12］陆添超，康凯．熵值法和层次分析法在权重确定中的应用［J］．软件开发与设计，2009（2）:19－20．

［13］周霖仪，刘志成，何佳洲．层次-熵值组合赋权法在雷达辐射源识别中的应用［J］．指挥控制与仿真，2009，31（1）:27－29．

［14］魏道江．灰色关联分析在施工企业投标项目选择中的应用［J］．襄樊学院学报，2009，30（5）:41－44．

［15］张传友．灰色关联决策理论在工程投标项目选择中的应用［J］．基建优化，2006，27（1）:11－13．

［16］杨海玲．基于灰色关联分析的图书馆中文图书采购招标评价［J］．现代情报，2010，30（4）:148－150．

［17］郑玉彬，韩峰，马艳华．改进灰色关联度模型在设备选择中的应用［J］．机床与液压，2009，37（9）:41－43．

Application of grey relational model in pre-bid decision-making: based on hierarchy-entropy combined weight-assigning

CUI Dong-hong，SHANG Si-tong
（School of Management，Shenyang University of Technology，Shenyang 110870，China）

In the face of multiple projects in construction market，it is the practical requirement of the construction contracting market that scientific，rational and easily-implementing bidding decision-making methods are applied by the contractors．Based on it，the improved analytic hierarchy process（IAHP），entropy method and gray relational theory and their application are introduced in bidding decision-making of construction engineering project．According to the actual situation of engineering，the pre-bid decision-making indicator system is established，the weights are determined by hierarchy-entropy combined assigning method，and multiple projects are evaluated by improved grey relational model based on it．This method is validated by engineering examples，which proves that it can better overcome the limitation of single method，choose the best project，and make the bidding decision-making more fair and scientific．

construction contracting;bidding decision-making;analytic hierarchy process（AHP）;entropy method;hierarchy-entropy combined weight-assigning;gray relational model

C 934;F 284

A

1674－0823（2012）02－0149－06

2010－12－13

沈阳市政府科学基金项目（1091199－5－00）。

崔东红（1956－），女，辽宁沈阳人，教授，主要从事项目管理与评价等方面的研究。

* 本文已于2011－06－21在中国知网优先数字出版，DOI为CNKI:21－1558/C．20110621．1212．012，http://www．cnki．net/kcms/detail/21．1558．C．20110621．1212．012．html．

（责任编辑:吉海涛）