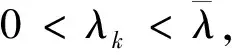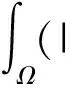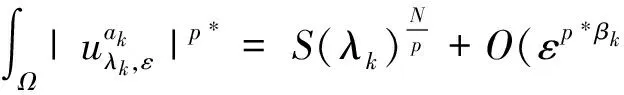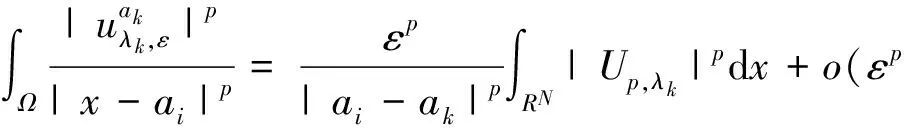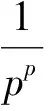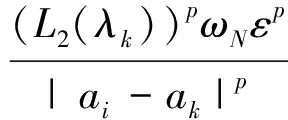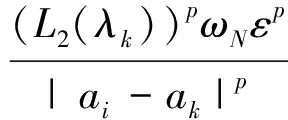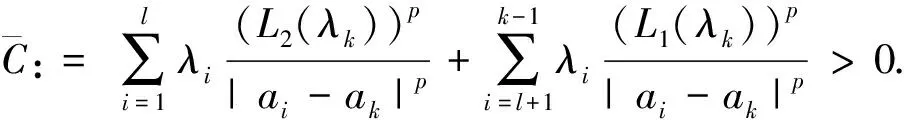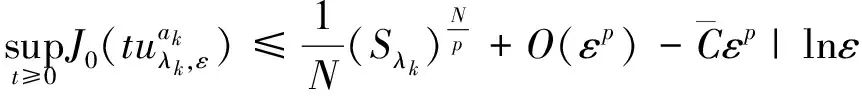带有临界Sobolev指数和位势的拟线性方程的正解
2012-01-03康东升李智萍
康东升,李智萍,方 达
(中南民族大学 数学与统计学学院,武汉 430074)
1 问题的引入
本文研究下列椭圆方程:
(1)


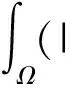

则称u为方程(1)的解. 求方程(1)的解等价于求

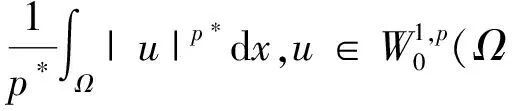
的临界点.
研究方程(1)涉及到Hardy不等式[1,2]

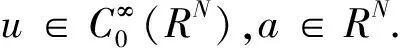
近些年来,有作者研究含有Hardy项的椭圆极限问题:
(2)
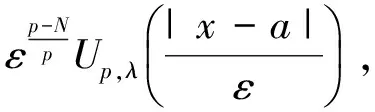
满足:
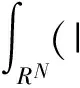
(3)
其中S(λ)是与方程(2)对应的最佳Sobolev常数,Up,λ(x)是方程(2)的径向解, 满足:

其中C1,C2是关于λ,p和N的正常数,a(λ)和b(λ)是函数f(t)=(p-1)tp-(N-p)tp-1+λ(t≥0)的零点,满足:
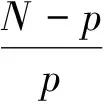
并且存在正常数L1(λ)和L2(λ),使得:
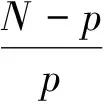
(4)
以上结果对于研究问题(1)非常重要.
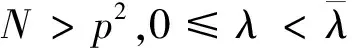
β:=b(λ)-δ,βi:=b(λi)-δ(i=1,2,…,k).
(5)
在本文中,我们假设:
(H1)λ1≤λ2≤…≤λk,k≥2 且存在l∈{i=0,1,2,…,k-1}, 使得:
λl≤0<λl+1≤λl+2≤…≤λk,(l0=0),
本文的主要结果如下.
定理1 假设(H1),当1
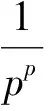
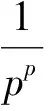
则方程(1)至少存在一个正解.

2 正解的存在性
下列引理给出了泛函J0的Palais-Smale条件.
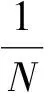
证明应用集中紧性原理[4,5]和文[6]中的思路,可以得到需要的结论,过程略.
下面我们研究(3)式的极值函数.令:
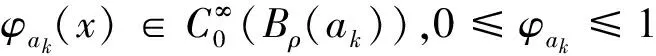
0<ρ 则存在正常数C1和C2使得∀x∈Bρ(ak),1≤i≤k-1,有C1≤|x-ai|≤C2成立. (6) (7) (8) (9) (10) 其中L1(λk)和L2(λk)是(4)式中定义的常数,ωN是RN中单位球的体积. 证明文献[6]已经证明了(6)和(7)式,我们现在证明(8)和(10)式. (9)式的证明和(10)式的证明类似. 先研究b(λ)的性质. 容易验证: f(t)=(p-1)tp-(N-p)tp-1+λ,t∈[0,+∞). 有唯一的最小值点δ=(N-p)/p,且f(t)在(0,δ)上单调递减,在(δ,+∞)上单调递增. A1(ε)+A2(ε)+A3(ε). (11) 下面我们估计A1(ε),A2(ε)和A3(ε)的值. (12) (13) 其中 另一方面, O(εp+pb(λk)-N)=o(εp). (14) (15) 注意到(15)式中最后一个积分存在.又由 (16) 可知(15)式中倒数第2个积分收敛.由(15)和(16)式得: (17) 另一方面,由(15)和(16)式得: A2(ε)=O(εp),A3(ε)=O(εp). (18) 引理3 在定理1的假设条件下, 有: (19) 证明注意到: 且 因此, (i)首先考虑下面情形: 则pb(λk)-N+p>p.由引理2可得: 当ε充分小时可得(19)式. 则pb(λk)-N+p=p. 由引理2得: 当ε充分小时可得(19)式. 引理3证毕. 定理1的证明根据引理1~引理3,应用山路引理[7,8]和极大值原理[9], 可以得到定理1的结论,详细过程也可参见文[10]中定理1.3 的证明,这里略去. [1]Azorero J, Peral I. Hardy inequalities and some critical elliptic and parabolic problems[J]. J Differential Equations, 1998,144(2):441-476. [2]Hardy G, Littlewood J, Polya G. Inequalities[M]. Cambridge: Cambridge University Press, 1988:239-243. [3]Abdellaoui B, Felli V, Peral I. Existence and non- existence for quasilinear equations involving thep-Laplacian[J]. Boll Unione Mat Ital Sez B, 2006, 9(2):445-484. [4]Lions P L .The concentration compactness principle in the calculus of variations, the limit case (I)[J]. Rev Mat Iberoamericana,1985,1(1):145-201. [5]Lions P L. The concentration compactness principle in the calculus of variations, the limit case (II)[J]. Rev Mat Iberoamericana,1985,1(2):45-121. [6]Han P.Quasilinear elliptic problems with critical expon- ents and Hardy terms[J]. Nonlinear Anal,2005,61(5):735-758. [7]Ambrosetti A, Rabinowitz H. Dual variational methods in critical point theory and applications[J]. J Funct Anal, 1973,14(2):349-381. [8]Brezis H, Nirenberg L. Positive solutions of nonlinear elliptic equations involving critical Sobolev exponents[J]. Comm Pure Appl Math, 1983,36(4):437-477. [9]Vazquez J L. A strong maximum principle for some quasilinear elliptic equations[J]. Appl Math Optim, 1984,12(1):191-202. [10]Cao D, Han P. Solutions to critical elliptic equations with multi-singular inverse square potentials[J].J Differential Equations, 2006,224(2):332-372.