一种新的正弦波频率估计算法

张刚兵，钱显毅

（常州工学院 电子信息与电气工程学院，江苏 常州 231002）

一种新的正弦波频率估计算法

张刚兵＊，钱显毅

（常州工学院 电子信息与电气工程学院，江苏 常州 231002）

研究了高斯白噪声条件下大样本点单一正弦波信号的频率估计方法.首先利用离散傅里叶变换确定频率粗估计，然后以该值为参考频率构造本地信号，将原信号下变频至基带，对基带信号分段求和，能得到一个新的正弦波信号，该信号的频率为真实频率与参考频率之差，最后利用最小二乘法估计新信号的载频，修正粗估计值就能得到原信号频率的最优估计.推导了算法的渐近方差与克拉美－罗限之间的关系.仿真结果表明，本算法能适用于整个频段范围，频率估计的精度接近正弦波频率估计的克拉美－罗限.

大样本；离散傅里叶变换；相关积累；频率估计

正弦波频率估计算法广泛应用于雷达、通信以及电子对抗等信号处理领域.Rife［1］最先提出了被加性复高斯白噪声污染的正弦波信号频率估计算法——最大似然（Maximum Likelihood，ML）估计，虽然其性能接近正弦波频率估计的克拉美－罗限（Cramer－Rao Lower Bound，CRLB），但需要进行一维频率搜索，计算量太大，不利于工程采纳.多位学者对正弦波信号频率估计问题作了进一步研究，相继提出了多种频率估计算法.这些算法大致可分为两类，一类是基于谱线插值，另一类是基于相位信息.

文献［2］利用信号的最大两根谱线插值进行频率估计，即Rife算法.当信号频率位于量化频率附近时，由于插值方向错误，会导致频率估计性能下降.针对这一问题，文献［3］先对信号进行频移，使新信号的频率位于两个相邻量化频率点的中心区域，提出了修正Rife算法，再以该算法的估计值为初始值进行一次牛顿迭代（Sinusoid Frequency Estimation Based on Newton's Method，SFENM）.当初始值位于收敛区域时，迭代收敛，其性能稳定，否则会导致频率估计精度下降.文献［4］提出了基于DFT相位的正弦波频率和初相估计方法（Based on Phase of DFT，BPDFT），利用分段DFT频谱的相位差消除了初相对频率估计的影响且避免了相位测量模糊问题.文献［5］指出，当信号真实频率与DFT量化频率差为某一范围时Rife算法精度不高，并研究了噪声背景中插值FFT估计正弦信号频率估计的问题.文献［6］利用与最大谱线对应的量化频率点相差半个量化频率的两根谱线进行插值，提出了一种迭代插值（（Iterative Frequency Estimation by Interpolation on Fourier Coefficients，IFEIFC））频率估计算法，性能接近克拉美－罗限.

Tretter［7］将加性复测量噪声等效为加性实相位噪声，利用最小二乘法对展开的相位估计信号的频率.高斯噪声条件下的最小二乘估计等价于最大似然估计，因此，文献［7］的算法在高斯噪声条件下的性能接近正弦信号频率估计的克拉美－罗限，但该算法模型成立的信噪比门限约为10dB，降低了其在低信噪比条件下的性能.为了避免相位展开，文献［8］利用相位平均和相位加权平均提出了基于相位差分的频率估计算法，在高信噪比条件下的性能与最小二乘法相当，也接近克拉美－罗限，但该算法也不适用于信噪比低于10dB的场合.文献［9－11］相继提出了3种基于信号自相关函数的频率估计算法，虽然改善了信噪比门限附近的性能，使之不会急剧恶化，但高信噪比条件下的性能却无法接近克拉美－罗限，甚至还会缩小频率估计范围［11］.文献［12］反复利用低通滤波、抽取，线性预测以及数字差拍变频进行频率估计（Iterative Lin－ear prediction，ILP），大大降低了算法的信噪比门限，信噪比门限以上的性能最多超过克拉美－罗限0.7dB.文献［13］多次利用自相关函数进行频率估计（Autocorrelation－based algorithm，AA），当信号样本长度为1 024时，其频率估计的均方根误差比克拉美－罗限大0.14dB.

当信号样本点数较大时，受硬件条件的限制，难以一次性对全部接收信号进行处理.如果先将信号分成等长的L段，再对每段信号分别进行频率估计，最后对各频率估计值取算术平均，那么只能得到非相干频率估计值，其估计方差仅为各段方差的L分之一，与整段信号频率估计的克拉美－罗限（为各段频率估计方差的L3分之一）相差甚远，此时的估计精度可能难以满足系统的性能指标.为了能估计大样本点信号的频率参数，同时保证参数估计的精度满足系统设计要求，必须研究新的频率估计方法.

受文献［3－6］的启发，本文利用离散傅里叶变换（Discrete Fourier Transform，DFT）的信噪比增益作用降低信噪比门限，结合高斯噪声条件下最小二乘等价最大似然的特性，提出了一种正弦波频率估计算法.首先利用离散傅里叶变换得到频率粗估计值，然后以该值作为参考频率将原信号下变频至基带，分段求和后能得到一个新的正弦波信号.以该正弦波的频率修正参考频率就能得到原信号的频率估计值.与基于相位信息的算法相比，本算法的信噪比门限更低、均方误差更接近克拉美－罗限，与基于谱线插值的算法相比，计算效率更高.

1 算法介绍

设信号模型为

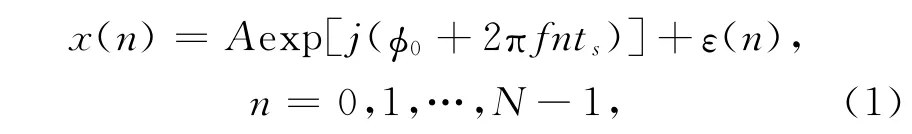
式中，A为信号的幅度，φ0为初始相位，f为信号的频率，ts为采样间隔，N为信号样本点数.ε是均值为0、方差为σ2的复高斯白噪声，定义信号的信噪比（signal－to－noise ratio，SNR）为SNR＝A2／σ2.

对式（1）定义的正弦波采样序列x（n），假定已得到信号频率f的粗估计值＾f0，现构造序列

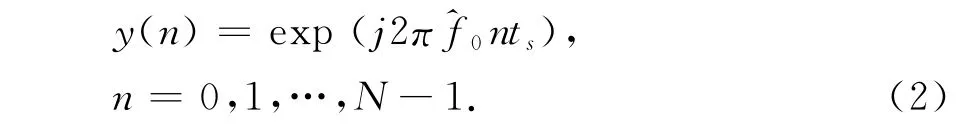
将（1）式和（2）式共轭相乘

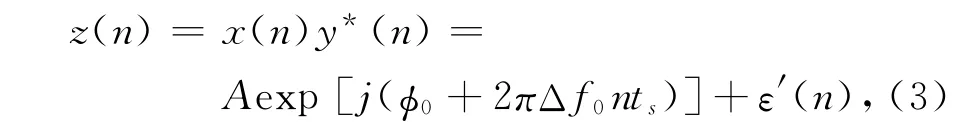
式中，ε′是均值为0、方差为σ2的复高斯白噪声，Δf0＝f－为粗估计的误差.

将式（3）表示的信号z（n）按M点分为一组并求和，能得到一个点数为L＝N／M的新序列，假设N／M为整数，有

式（4）中的S（m）是一个频率为Δf0、采样间隔为Mts、样本点数为L点的正弦波序列，对S（m）进行频率估计可得到频偏Δf0的估计值Δ＾f0，修正粗估计能得到信号频率f的精确估计.无模糊估计频率要求频偏Δf0满足奈奎斯特采样定理，即

序列S（m）的信噪比SNRout≃MA2／σ2＝M×SNR，与正弦波采样序列x（n）相比，此时的信噪比增益提高了10lg MdB.累加点数M越多，信噪比增益越大，频偏Δf0估计的信噪比门限越低.Tretter在文献［7］中指出，当复正弦序列的输入信噪比远远大于1时，加性复测量噪声可近似为等效的加性实相位噪声，且相位噪声的方差为正弦波输入信噪比倒数的一半.当原测量信号信噪比不太小、信号样本点数较大时，经过求和积累后，式（4）的信噪比SNRout有可能远远大于1.因此，式（4）可近似为

式中，ζm是均值为0、方差为1／（2SNRout）的实高斯白噪声.

高斯白噪声条件下的最小二乘估计等价于最大似然估计，如果能得到序列S（m）无模糊的相位值φm，就能用最小二乘估计得到频偏Δf0的最优估计.设

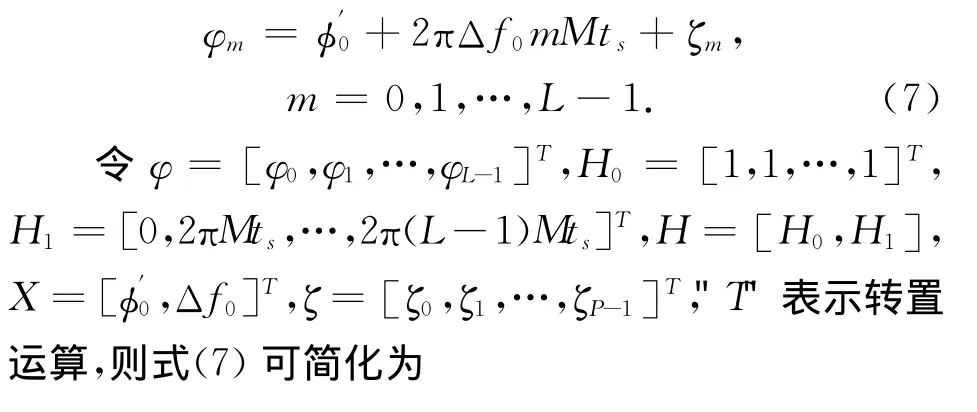
式（8）中X的最小二乘估计为

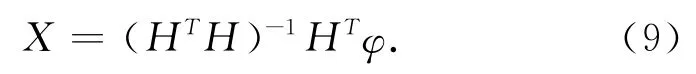
利用频偏的估计值修正频率粗估计就能得到信号频率的精确估计，综合以上分析，本算法的实现步骤为

2）按照公式（2）、（3）、（4）得到序列S（m），m＝0，1，…，L－1；

3）利用文献［7］的算法对S（m）进行载频估计，得到频偏Δf0的估计值Δ

4）利用频偏Δf0的估计值得到频率估计值

2 性能分析

现从渐近方差（Asymptotic Error Variance，AEV）以及计算量对本算法进行定量分析.

2.1 渐近方差（AEV）

利用最大谱线对应的量化频率点作为频率粗估计，在不出现频率模糊的条件下，粗估计误差满足

对式（3）表示的信号z（n）进行M 点累加以后，新序列的信噪比增加了10lg（M）dB，M 越大，信噪比增益越大，影响频偏估计的信噪比门限就越低.累加之后要求信号S（m）有两个以上的样本点，M 的取值必须满足M ≤N／2，利用式（10），有

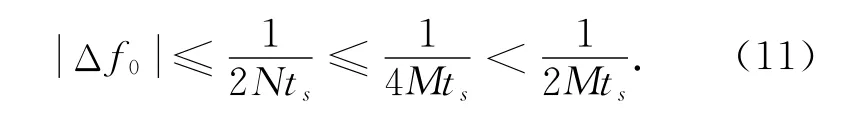
因此，累加之后能满足式（5）对无模糊频率估计的要求.

频率估计的精度由频偏Δf0的估计精度决定，而频偏估计是无偏估计，估计的均方误差为［7］

式中，E（·）表示取数学期望.

正弦波信号频率估计＾f的克拉美 －罗限（CRLB）为［1］

由式（12）和式（13）有

从式可以看出，累加点数M越大，性能损失越大，当M＝N／2时，性能下降最严重，此时的性能与克拉美－罗限相差1.25dB.但当M分别为N／4和N／8时，累加求和后的信号样本分别为4点和8点，性能相对克拉美－罗限分别下降0.28dB和0.07dB.在M≪N的条件下，本算法的均方误差与克拉美－罗限相等.

2.2 计算量分析

现分析本算法需要的计算量，假设N是2的整数次幂.在频率粗估计时利用快速傅里叶变换（Fast Fourier Transform，FFT）确定信号的频谱，需要N／2·log2N次复数乘法、Nlog2N次复数加法，确定最大谱线的位置需要N次复数乘法，式（4）需要N次复数乘法，式需要N（M－1）／M复数加法，获得相位需要N／M次反正切运算、N／M次相位展开，估计频偏则需要N／M次实数乘法和N／M－1次实数加法，作一次迭代需要N次复数乘法、N（M－1）／M复数加法、N／M 次反正切运算、N／M 次相位展开、N／M次实数乘法和N／M－1次实数加法.

3 仿真结果分析

为了验证本算法的测频性能，对其进行计算机仿真，信号样本点数为1 024，采样频率为100MHz，信噪比为0dB，累加点数M为128，信号频率从25MHz开始，到25MHz＋1／（2 NΔt）结束，将频率变化范围等分20份，每个离散频率点上各仿真2 000次.其均方根误差与克拉美 －罗限之比随频率变化的性能曲线如图1所示.

图1的仿真结果表明，基于自相关函数相位信息的频率估计算法的均方根误差最大，基于谱线迭代插值和以修正Rife算法估计值为初值进行一次牛顿迭代的频率估计算法性能相当，都能在整个频段范围内进行频率估计.

下面验证本算法在不同信噪比条件下的性能.采样频率为100MHz，信号的频率为f＝21.123 42MHz，信号样本点数N为1 024，累加点数M为128.对本算法的性能进行仿真，给出了各算法在相同条件下的性能对比，每种条件下各进行2 000次独立的仿真.均方根误差（RMSE）与信噪比（SNR）之间的关系如图2所示.图中给出了各算法的均方根误差及克拉美－罗限，图中横轴为线性坐标，纵轴为对数坐标.

图1 测频范围性能对比Fig.1 Comparison of frequency range

图2 正弦波频率估计的性能曲线Fig.2 Performance comparison of frequency estimation

图2的仿真结果表明，本算法与文献［6］算法一样，具有相同的信噪比门限，且都低于文献［3－4－12－13］算法.因此，本算法对信噪比要求更低，能估计较低信噪比条件下信号的频率.在较低信噪比条件下，牛顿迭代的初始值位于收敛区域之外，迭代不收敛，此时的估计性能不如本算法.随着信噪比的增加，初始值进入收敛区域，迭代后的性能接近克拉美－罗限.文献［12－13］都是基于迭代自相关函数估计信号的频率，其信噪比门限均高于基于DFT的频率估计算法.在整个信噪比变化区间内，本算法的均方根误差都接近克拉美－罗限，表明本算法性能稳定，对信噪比变化不敏感.

4 结束语

本文提出了一种适用于单一信号的频率估计算法，本算法具有较低的信噪比门限，其性能均匀分布在整个测频范围内.当累加求和后的信号样本点数为8时，频率估计的均方误差相对克拉美－罗限下降0.07dB.当累加后的信号样本点数远小于原测量信号样本点数时，本算法的均方误差与克拉美－罗限相同.考虑信噪比门限、测频范围以及估计性能，本算法都优于基于相位和自相关函数的频率估计器，因此，本算法具有一定的工程应用价值.

［1］Rife D C，Boorstyn R R.Single－tone parameter estimation from discrete－time observations［J］.IEEE Trans on Information Theory，1974，20（5）：591－598.

［2］Rife D C，Bowstyn R R.Multiple tone parameter estimation from discrete rime observation［J］.Bell Syst Tech J，1976，55（9）：1389－1410.

［3］邓振淼，刘 渝.正弦波频率估计的牛顿迭代方法初始值研究［J］.电子学报，2007，35（1）：104－107.

［4］齐国清，贾欣乐.基于DFT相位的正弦波频率和初相的高精度估计方法［J］.电子学报，2001，29（9）：1164－1167.

［5］齐国清，贾欣乐.插值FFF估计正弦信号频率的精度分析［J］.电子学报，2004，32（4）：625－629.

［6］Aboutanios E，Mulgrew B.Iterative frequency estimation by interpolation on Fourier coefficients［J］.IEEE Trans on Signal Processing，2005，53（4）：1237－1242.

［7］Tretter S.Estimating the frequency of a noisy sinusoid by linear regression［J］.IEEE Trans on Information Theory，1985，31（6）：832－835.

［8］Kay S M.A fast and accurate single frequency estimator［J］.IEEE Trans on Acoustics，Speech，and Signal Processing，1989，37（12）：1987－1990.

［9］Fitz M P.Further results in the fast estimation of a single frequency［J］.IEEE Trans Communications，1994，42：862－864.

［10］Luise M，Reggiannini R.Carrier frequency recovery in alldigital modems for burst－mode transmissions［J］.IEEE Trans Communications，1995，43：1169－1178.

［11］Fowler M L，Johnson J A.Extending the threshold and frequency range for phase－based frequency estimation［J］.IEEE Trans on Signal Processing，1999，47（10）：2857－2863.

［12］Brown T，Wang M M.An iterative algorithm for singlefrequency estimation［J］.IEEE Trans on Signal Processing，2002，50（11）：2671－2682.

［13］Xiao Yang－Can，Wei Ping，Tai Heng－Ming.Autocorrelation－based algorithm for single－frequency estimation［J］.Signal Processing，2007：1224－1233.

Novel frequency estimation method for sinusoidal signal

ZHANG Gangbing，QIAN Xianyi
（Changzhou Institute of Technology，School of Electronic Information and Electric Engineering，Changzhou，Jiangsu 231002）

A novel algorithm for frequency estimation of sinusoid with many samples in the complex white Gaussian noise was proposed.A coarse frequency estimate was obtained through discrete Fourier transform and a sequence was constructed with the coarse frequency estimate being a reference frequency.Then the original sequence was converted into baseband by down－conversion.A new sinusoid was acquired after correlation accumulation，of which the frequency was the difference between the original frequency and reference one.Linear regression made it possible to get the optimal frequency difference estimate.The relationship between the asymptotic error variance（AEV）and the Cramer－Rao lower bound（CRLB）was derived.Simulation results show that the performance of the proposed algorithm approaches the CRLB of the sinusoidal signal when the signal－to－noise ratio（SNR）is higher than the SNR threshold.

large sample；DFT；correlation accumulation；frequency estimation

TN911

A

1000－1190（2012）01－0040－05

2011－07－10.

江苏省高校自然科学基金项目（10KJD480003）；常州工学院校级基金项目（YN1101）.

＊E－mail：caeppub＠sohu.com.