基于轮廓检测的自然图像分割

杨得国，万红娟，杨 勐

（西北师范大学 数学与信息科学学院，兰州 730070）

基于轮廓检测的自然图像分割

杨得国＊，万红娟，杨 勐

（西北师范大学 数学与信息科学学院，兰州 730070）

提出一种基于轮廓检测的自然图像分割方法，该方法结合了MDL（最小描述长度）统计技术和用变分水平集函数求解活动轮廓模型的图像分割方法.该方法可有效的分割出图像中最突出的感兴趣目标，实验表明本方法与当前技术相比分割效果更好.

活动轮廓；水平集；图像分割；最小描述长度

轮廓检测和图像分割是计算机视觉领域两个最基本的关键问题.给定一幅图像，希望找到一条封闭轮廓从背景中分割出最突出的对象.界定轮廓有两个标准：自然轮廓有光滑的形状，轮廓将图像分成各具特性的区域.由此产生两种轮廓检测的方法［1］：基于边缘和基于区域的方法.基于边缘的方法，使用边缘检测算子［2-3］，先检测图像中的边缘点，然后按一定的策略连接成轮廓，从而构成分割区域.基于区域的方法［4］，统计了轮廓分割出的图像区域的特征的相似性与均匀性.全局轮廓检测方法是基于能量函数［5］或者Bayesion／MDL（最小描述长度）标准［6-8］，该方法首先给出一个模型，如活动轮廓模型，一条能量递减曲线，由轮廓自身特征决定的内部能量和图像特征决定的外部能量共同支配，在能量最小的原则下移动并最终停止于感兴趣区域轮廓附近.近年来，活动轮廓技术得到了不断的改进和发展，并在图形图像、模式识别、计算机视觉等领域得到了广泛的应用.

本文结合基于MDL的全局图像统计信息，修正变分水平集函数进而实现轮廓检测，完成对自然图像的分割.实验表明本文方法能较好的分割出自然图像中最凸出的感兴趣区域.

1 水平集方法

基于几何活动轮廓模型的变分水平集分割技术是目前广泛研究的一种图像分割方法［5，9-10］，通过一个高维函数曲面来表达低维的轮廓线，即将轮廓线表达为高维曲面的零水平集，并将轮廓曲线的运动方程转化为高维水平集函数的偏微分方程.该方法用轮廓曲线的几何性质，建立轮廓运动的能量函数，用水平集函数表达轮廓运动.定义轮廓为C，用水平集函数φ（t，x，y）的零水平集表示为C（t）＝｛（x，y）｜φ（t，x，y）＝0｝.函数φ的演化公式为

其中，F是速度函数，与图像数据信息和水平集函数φ有关.传统的水平集方法需要将水平集函数φ初始化为符号距离函数φ0，每次迭代之后都需要重新初始化符号距离函数，计算量很大，当初始水平集函数离符号距离函数较远，则不能将φ0函数重新初始化为符号距离函数.Li等人提出一种无需重新初始化的模型［9］，该模型采用变分方法将水平集函数强制转换为一符号距离函数，有效消除了重新初始化这一步骤，本文采用该方法求解水平集函数的演化.

Li方法的变分方程为

公式右边第一项为符号距离函数约束项，其中μ＞0，该参数控制φ的导数到符号距离函数的罚约束，P（φ）是满足｜▽φ｜＝1的函数，表示函数φ到符号距离函数的距离.右边第二项Ein（φ）是内部能量项，使得零水平集函数φ向感兴趣区域轮廓边界移动.类似与参数活动轮廓模型定义

其中，λ，υ为常数，υ控制演过过程中轮廓线的收缩或扩张，Lg（C）为梯度信息加权的轮廓长度，Ag（C）为区域面积.上述能量项用水平集函数表示为

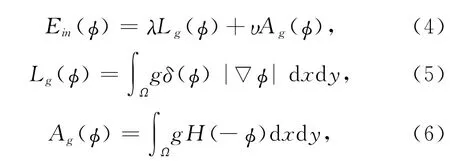
其中，g为边缘停止函数，H（x）是Dirac函数，λ为常数，一般取1到4之间的值.综上所述，Li方法提出的能量函数为

求解上述能量函数的极小化，用变分法求解得其关于E的一阶变分方程为

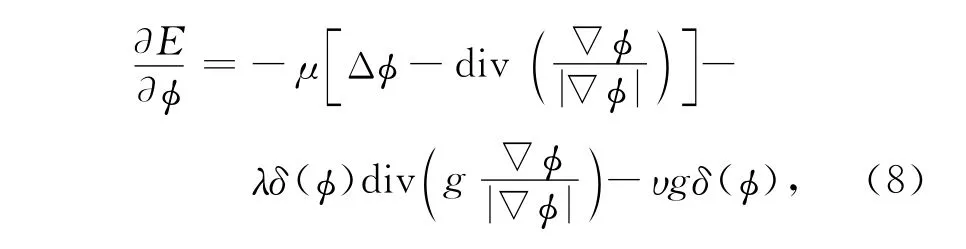
Li方法利用图像梯度信息构造边缘停止函数，容易将背景梯度变化较大位置误判为感兴趣区域轮廓边界，本文修正变分水平集函数进而实现轮廓检测完成对自然图像的分割.

2 基于MDL的轮廓检测

leclerc等人介绍了一种基于最小描述长度（MDL，minimum description length）的算法，用一个描述长度函数来描述图像的区域和边界信息，以此作为目标函数，通过极小化描述长度从而得到分割结果.Wang基于MDL统计模型提出一种新的轮廓能量函数［1］，介绍了一个感知能量项说明轮廓在分割处的变化剧烈，该能量项使图像分割效果更好，根据轮廓内外前景与背景的亮度熵和轮廓线的曲率熵定义分割区域间的“相关度”，使用熵编码长度O（C）表示轮廓C的组织力（信息量）.本文方法没有采用曲率熵.O（C）公式如下：

其中，hf和hb分别是前景与背景直方图高斯平滑后的统计特征，Nf和Nb分别是两区域像素个数的统计.

由于图像在边界轮廓处的剧烈变化，类似于边缘检测，Wang用能量函数O（C）的一阶偏导数

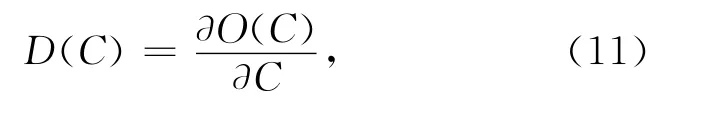
图1 花瓶的O（C）与D（C）（a）原图；（b）红色轮廓与O（C）相关，蓝色轮廓与D（C）相关；（c）O（C）和D（C）的函数曲线图Fig.1 A case of O（C）and D（C）of the vase

捕捉轮廓形状或位置的微小改变，反映O（C）随轮廓C移动时的变化.当目标前景与背景的差异最大时，D（C）达到最大值.Wang方法的优势在于：结合了图像的全局和局部信息，避免了模型估计，克服了非匀质区域的过分割问题.（11）式可离散化为

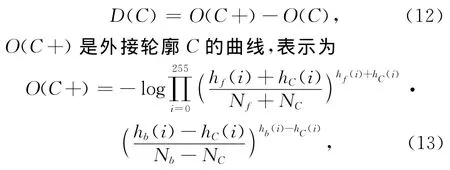
其中，hC是基于轮廓C 的直方图经高斯模型化统计特征，NC是轮廓C上所有像素点的数目.

O（C）和D（C）在轮廓检测中的重要作用可以通过图1直观反映出来，其对图像分割的感知意义是本文算法提出的原因，算法没有直接使用D（C），而是使用其变分优化后的值对轮廓予以修正.

图1花瓶与背景的亮度直方图相似，编码标准公式（10）不能表示任何边界，D（C）在轮廓边界位置成功的给出了局部最大值.红色和蓝色的轮廓线是人工绘制的视觉感知较好的轮廓边界曲线.

3 修正的变分水平集方法

综上所述，本文结合基于MDL的全局图像统计信息，亮度熵编码长度，修正变分水平集函数实现图像分割.方法如下.

1）初始化

定义Ω0为图像Ω的子集，∂Ω0为Ω0的轮廓线上所有像素点的集合.初始化水平集函数φ0定义为

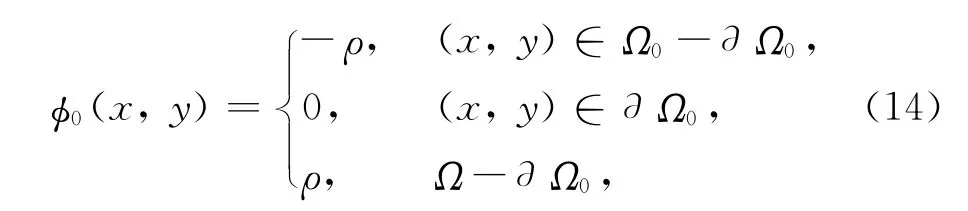
其中，ρ为常数，且ρ＞2ε，ε为规则化Dirac函数δε的宽度.

令（10）式中轮廓C＝∂Ω0，以C为边界，ΩΩ0为背景，Ω0为前景；（12）式中以轮廓C＋为边界，Ω－Ω0－∂Ω0为背景，Ω0＋∂Ω0为前景.

2）计算修正量

定义特征函数为

其中，υ是轮廓C上的像素点.其所得出的结果为水平集函数∂Ω0演化后轮廓的修正量.使得轮廓跃过图像背景梯度变化较大、独立的小区域继续向感兴趣目标演化.

3）差分求解水平集函数

规则化Dirac函数δ（φ）通常定义如下.

求解方程（17）所得的水平集函数的零水平集即为感兴趣区域轮廓.数值计算中，使用差分方法

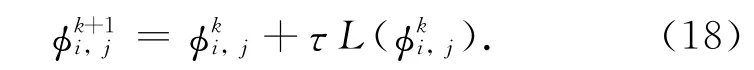
4）判断熵编码长度能量函数是否足够小，否则修正水平集函数.

本文算法由于需要计算图像的统计信息，计算量有所增加，但是分割结果明显好于Li方法.在下面的实验中取参数ρ＝4，ε＝1.5能满足多数自然图像的分割，适当改变参数可以获得好的分割结果.

4 实验结果与分析

应用上述方法，在 Windows XP系统Matlab环境下进行自然图像的轮廓检测及其分割.图像可以是灰度图像也可以是彩色图像.

图2 两个感兴趣区域的图像分割结果（a）初始轮廓；（b）本文方法迭代100次分割结果；（c）Li方法迭代100次分割结果；（d）Wang方法分割结果Fig.2 Segmentation results of an image with two regions of interest

图2为说明本文算法与Li方法、Wang方法的异同，用一幅包含两个感兴趣区域的灰度图像进行实验.本文方法迭代100次已经很好的检测出轮廓，分割出两个目标区域.Li方法迭代100次两个目标仍为一体，Wang方法运行时间长、迭代次数多，却只保留了面积较大的目标.

图3 一些自然图像的分割结果（a）本文方法；（b）本文方法分割结果；（c）Li方法；（d）Wang方法Fig.3 Segmentation results of some natural images

图3初始轮廓线由公式（14）得出，将轮廓线初始位置设在感兴趣区域附近，演化速度会更快，分割效果会更好.本实验中彩色图像使用Lab空间L分量，灰度图像使用其亮度信息.本文算法能很好的检测出目标轮廓、分割出目标区域，如士兵、女士、冲浪者、坦克，对花瓶产生了过分割.Li方法只对花瓶的分割很好，其它分割效果不如本文.Wang方法运算量非常大，耗时长达数分钟，分割效果也不尽人意，且其需要人为改变参数才能得到较好的效果.

5 结论

本文方法能较好的检测出自然图像中最突出的感兴趣区域的轮廓，完成图像的分割.但是由于采用水平集方法求解活动轮廓，且统计了图像的全局信息，计算量很大，存在分割不准确问题.今后将对本文算法效率、性能进行进一步改进以更好地控制轮廓形状以得到较为理想的分割结果.

［1］Wang H，Oliensis J.Generalizing edge detection to contour detection for image segmentation［J］.Computer Vision and Image Understanding，2010，114（7）：731－744.

［2］Canny J.A Computational approach to edge detection［J］.Readings in Computer Vision：Issues Problems Principles and Paradigms，1987，184：87－116.

［3］Martin D R，Fowlkes C C，Malik J.Learning to detect natural image boundaries using local brightness，color，and texture cues［J］.Pattern Analysis and Machine Intelligence IEEE Transactions，2004，26（5）：530－549.

［4］张建伟，陈允杰，夏德深.基于直方图的快速 Mumford－Shah模型 MRI分割［J］.中国图象图形学报，2005，7（10）：838－843.

［5］Chan T F，Vese L A.Active contours without edges［J］.Image Processing IEEE Transactions，2001，10（2）：266－277.

［6］Zhu S C，Yuille A.Region competition：Unifying snakes，region growing，and Bayes／MDL for multiband image segmentation［J］.Pattern Analysis and MachineIntelligence IEEE Transactions，1996，18（9）：884－900.

［7］Paragios N，Deriche R.Geodesic active regions and level set methods forsupervised texture segmentation［J］.International Journal of Computer Vision，2002，46（3）：223－247.

［8］Leclerc Y G.Constructing simple stable descriptions for image partitioning［J］.International Journal of Computer Vision，1989，3（1）：73－102.

［9］Li C M，Xu C Y，Gui C F，et al.Level set evolution without re－initialization：A new variational formulation［J］.Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition San Diego，2005：430－436.

［10］肖春霞，初 雨，张 青.高斯混合函数区域匹配引导的Level Set纹理图象分割［J］.计算机学报，2010，7（33）：1295－1304.

Natural image segmentation based on contour detection

YANG Deguo，WAN Hongjuan，YANG Meng
（College of Mathematics and Information Science，Northwest Normal University，Lanzhou 730070）

In this paper，we propose a new method of natural image segmentation based on contour detection.The algorithms combine the statistical techniques of minimizing MDL（Minimum Description Length）criterion which involves the whole image and the active contour model in a variational level set formulation.This method is effective to segment the most salient objects in the scene.Comparisons with other state－of－the－art approaches validate our method’s advantages.

active contour；level set；image segmentation；MDL

TP391.41

A

1000－1190（2012）01－0018－05

2011－06－13.

国家自然科学基金项目（61165002）.

＊E－mail：yangdeguo＠nwnu.edu.cn.