基于GRNN 的坡面径流输沙能力模型的试验研究

焦鹏，姚文艺，严军，肖培青，申震洲，杨春霞

(1.华北水利水电学院，450011，郑州;2.黄河水利科学研究院，450003，郑州)

土壤侵蚀预报模型对于定量评价水土保持效果，合理制订水土保持措施等具有重要意义。坡面径流输沙能力是建立土壤侵蚀过程模型的重要水力学参数，对模型的模拟预报精度有着重要影响。20世纪40 年代以来，众多学者通过试验研究、野外观测等手段对坡面径流输沙能力进行了大量研究，并采用力学机制研究、统计分析等方法，建立了一系列半理论、半经验和经验公式，如Govers 公式［1］、Everaert 公式［2］、Brahams 公式［3］等。由于研究对象的差异和率定资料的不同，坡面径流输沙能力公式在形式和适用范围上存在较大差异，同时一些参数难以准确获取和率定，使得公式不便于推广应用。

由于坡面水蚀的多种侵蚀形式和复杂侵蚀过程，坡面径流输沙能力的定量计算较为困难。研究［4－5］表明，神经网络可以逼近任意的非线性函数，能够模拟复杂的非线性系统。近年来，国内外一些学者［6－9］将神经网络理论用于河流的输沙能力研究，取得了较好的模拟预测结果;但该理论在坡面径流输沙能力方面的研究较少。笔者将神经网络理论用于坡面径流输沙能力研究，根据坡面径流输沙能力试验资料，使用平均影响值(mean impact value，MIV)方法分析、评价各因素对神经网络模型的影响，据此建立广义回归神经网络(Generalized Regression Neural Network，GRNN)模型，使用交叉验证优选模型参数，并结合Adaboost(Adaptive Boosting)算法对模型进行优化。

1 试验设计

1.1 试验装置

试验在黄河水利科学研究院“模型黄河”试验基地进行。试验土槽为长5 m、宽3 m、深0.6 m 的可调角度钢制土槽，使用PVC 板材将其分隔为3 个长5 m、宽1 m 的试验小区。土槽底部钢板上钻有直径5 mm 左右的透水孔，PVC 板材边壁粘有不同粒径的沙粒以消除不同介质间的边界影响。土槽上端连接水平稳流池，为整个坡面均匀地提供平稳水流;在土槽末端连接集流槽，用来集中和收集坡面径流。试验土槽见图1。

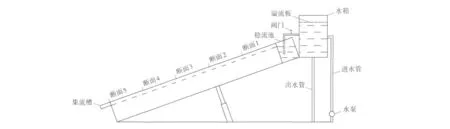
图1 试验土槽Fig.1 Experimental earth trough

1.2 试验方案

试验用土采用郑州邙山坡面表层黄土，颗粒组成见表1。将黄土过10 mm 筛后，采用分层填冲、压实的方法填土至50 cm 厚，控制土壤含水率在15%左右，土壤干密度在1.23 g/cm3左右。填土完成后，在坡段的上中下部分别使用环刀取样，计算土壤的平均密度，烘干后测定土壤干密度。试验前在坡面上洒水至表层土壤饱和，以保证每次试验的土壤前期含水量基本一致。本次试验采用坡度和流量2 个可控因素，坡度分别为10°、20°和30°，流量分别为1.0、2.0、3.0、4.0、5.0、7.5 和10.0 L/min，共有不同坡度和流量组合的21 个组次，每组进行2 次重复试验。试验开始前先对水平稳流池的来水流量按照试验所需进行率定，在坡面上标记5 个固定的观测断面后，开始进行坡面冲刷试验。在坡面产流以后开始计时，以2 min 为时间间隔使用水桶在集流槽处收集坡面径流，其间在观测断面使用染色剂法测量坡面径流流速，并取径流样以观察坡面径流含沙量的沿程变化，同时观测、记录坡面侵蚀形态的变化过程，每次试验进行30 min。

表1 供试土样粒径组成Tab.1 Particle distribution of the experimental soil

2 数据处理

2.1 影响因子选取

水流输沙能力的概念是针对河道中的泥沙输移趋于平衡时的不冲不淤状态而言，其表达形式与泥沙运动状况有关。根据河流动力学理论，径流输沙能力主要由水力条件和泥沙条件共同决定，可表示为如下函数形式［8－9］:

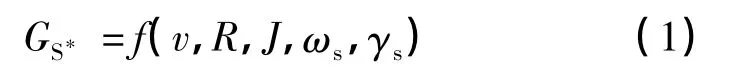
式中:GS*为径流输沙能力;v 为断面平均流速;R 为水力半径;J 为能坡;ωs为泥沙沉速;γs为泥沙密度。

在试验条件下，泥沙沉速ωs、密度γs为定值，故选择流速v、水力半径R 和能坡J 作为坡面径流输沙能力的影响因子。坡面径流输沙能力是由坡段的进出口边界条件和坡段内周界条件共同决定的。试验研究表明，流量是影响坡面径流输沙能力的重要参数［12］，针对坡面径流侵蚀和泥沙输移特征，考虑土壤干密度C、进口流量Qu、出口流量Qd对坡面径流输沙能力的影响。最终选择土壤干密度C、能坡J、进口流量Qu、出口流量Qd、水力半径R、流速v 等6 个影响因子作为模型的输入参量。

2.2 试验数据处理

研究［13］表明，神经网络模型的模拟预测精度与训练样本数目和分布有关，大量分布均匀的训练样本能够有效降低模型的预测误差。本研究以试验场次是否最终达到输沙平衡为判别标准，在不同坡度和流量的21 组试验中，选取每组试验达到输沙平衡的场次作为训练样本，将所有剩余场次中达到输沙平衡的6 场试验作为测试样本。使用试验后段坡面径流含沙量达到基本稳定时的实测平均值计算各影响因子和坡面径流输沙能力。

2.3 数据归一化

为消除模型输入输出中各参量数据量级差别对神经网络的影响，需要对输入输出矩阵进行归一化处理，使用极差归一化公式将所有数据变换至区间［0，1］。

3 建模理论与方法

3.1 MIV 因子分析

G.W.Dombi 等［12］提出用神经网络的平均影响值(MIV)来反映神经网络中权重矩阵的变化情况。MIV 是神经网络中分析变量相关性最好的指标之一，能够评价各自变量对因变量的影响大小，对输入网络的各影响因子进行分析、筛选，提高神经网络的模拟精度和收敛速度。

MIV 方法是将输入矩阵X 和输出矩阵Y 作为标准矩阵代入神经网络进行训练，分别对矩阵X 中的每一输入参量按比例增减形成比较矩阵X1和X2，将X1和X2代入训练好的神经网络计算得到相应的输出矩阵Y1和Y2，Y1与Y2差值的平均数即为平均影响值。MIV 值的符号表示该因子对神经网络输出的相关方向，绝对值大小表示其影响的相对重要性。使用包含6 个影响因子的训练样本数据，对每一输入参量进行基于GRNN 的MIV 分析，结果见表2。

表2 影响因子的MIV 值Tab.2 Mean Impact Value of the impact factors

结果表明，对于以上述各影响因子为输入参量、坡面径流输沙能力为输出参量建立的GRNN 模型，能坡、进口流量、出口流量、水力半径与模型输出呈正相关关系，干密度、流速与模型输出呈负相关关系，各因子对输出结果的影响大小依次为J ＞v ＞C ＞Qd＞Qu＞R。所选影响因子对模型输出的影响基本属于同一量级，因此，可以作为GRNN 坡面径流输沙能力模型的输入参量。

3.2 GRNN 建模

广义回归神经网络(GRNN)是美国学者D.F.Specht［13］提出的一种径向基神经网络，具有柔性网络结构和很强的非线性映射能力，适于解决非线性问题。GRNN 由输入层、模式层、求和层、输出层构成。

输入层由m 个神经元组成，其数目为输入向量X=［x1，x2，…，xm］T的维数，作用是直接传递变量至模式层。

模式层由n 个神经元组成，对应n 个训练样本X1，X2，…，Xn，神经元转移函数为

式中:X 为输入向量，Xi为第i 个神经元对应的训练样本，i=1，2，…，n;σ 为高斯函数的宽度系数。

求和层由2 类神经元构成，SD对所有模式层神经元的输出进行算术求和，其与模式层各神经元的连接权值为1;S1，S2…，Sk对所有模式层神经元的输出进行加权求和，模式层第i 个神经元与求和层第j个神经元的连接权值yij为第i 个输出样本Yi的第j个元素。SD与Sj的计算公式分别为

式中yij为模式层第i 个神经元与求和层第j 个神经元的连接权值，i=1，2，…，n，j=1，2，…，k。

输出层由k 个神经元组成，其数目为样本输出向量Y=［y1，y2，…，yk］T的维数，输出层神经元j 的输出即为预测结果的第j 个元素yj，其计算公式为

将包含6 个影响因子的向量X 作为输入，坡面径流输沙能力Y 作为输出，构建GRNN 模型。

3.3 GRNN 平滑参数优选

设随机变量x 和y 的联合概率密度函数为f(x，y)，已知x 的观测值为X，则y 相对于X 的回归，即条件均值为

应用Parzen 非参数估计，由样本x 和y 的观测值估算概率密度函数

式中:Xi和Yi分别为随机变量x 和y 的样本观测值，作为第i 个训练样本的输入和输出向量，i=1，2，…，n;n 为样本容量;m 为随机变量x 的维数;σ为高斯函数的宽度系数，即平滑参数。

将式(7)代入式(6)，化简得

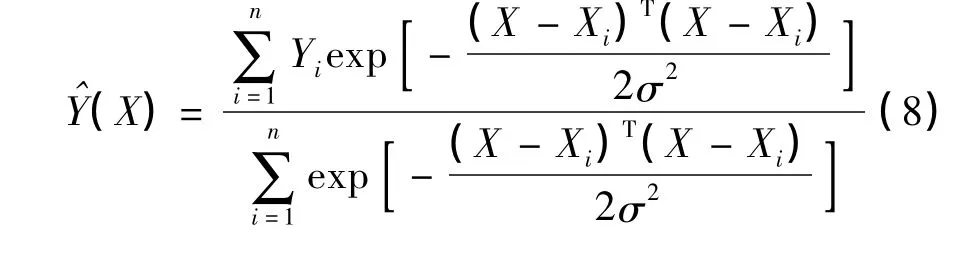
平滑参数σ 对GRNN 的预测性能影响较大，σ较大时估计值^Y(X)逼近所有训练样本因变量的均值，网络的泛化能力较强;σ 较小时估计值^Y(X)逼近与输入变量Euclid 距离最近的训练样本因变量，网络对训练数据的逼近效果较好。适中的平滑参数σ能够使GRNN 将所有训练样本因变量计算在内，且给予与输入变量Euclid 距离较近的样本因变量较大权重，综合考虑训练样本逼近与网络泛化能力的要求。

本文使用K 折交叉验证(K-fold cross－validation)对网络的平滑参数σ 进行优选，使GRNN 获得较好的逼近效果和泛化能力。研究［16］表明，K 取10是获得最好误差估计的恰当选择，故使用10 折交叉验证(10－fold cross－validation)测试所建GRNN，将10次测试中最小预测误差所对应的GRNN 作为该次交叉验证条件下的最优GRNN 模型，其平滑参数作为最佳平滑参数。

3.4 Adaboost 算法优化

Adaboost 是Y.Freund 等［17］提出的一种集成学习算法，可以有效提高单一学习器的泛化能力和模拟预测精度。本文采用连续型Adaboost 算法［18］，将10 折交叉验证中最佳平滑参数所对应的GRNN 模型作为该样本分类条件下的最佳弱预测器，并按照一定的权值集成10 个最佳弱预测器作为强预测器，即GRNN_Adaboost。对于n 个训练样本T 次训练过程的Adaboost 算法优化，其流程见表3。

表3 Adaboost 算法流程Tab.3 Algorithmic process of Adaboost

4 结果与分析

4.1 模型拟合与分析

以土壤干密度C、能坡J、进口流量Qu、出口流量Qd、水力半径R、流速v 作为输入参量，实测坡面径流输沙能力GS*作为输出结果，将训练样本数据代入GRNN_Adaboost 模型进行训练，模型拟合结果见表4。

表4 GRNN_Adaboost 模型训练结果Tab.4 Training results of GRNN_Adaboost model

由训练结果知，模型对所有训练样本的拟合误差平均值为13.88%。其中:坡度为10°的1 ～7 组训练样本的平均拟合误差为25.21%，最大拟合误差为第3 组的69.33%;坡度为20°的8 ～14 组样本的平均拟合误差为8.81%，最大拟合误差为第8 组的21.94%;坡度为30°的15 ～21 组样本的平均拟合误差为7.60%，最大拟合误差为第19 组的16.95%。研究［19］表明，坡面侵蚀方式对坡面径流输沙能力影响较大。坡度为10°时，坡面径流能坡较小，坡面未形成细沟或细沟未贯通试验观测断面，使得训练样本包含了面蚀和沟蚀等不同侵蚀形式的信息，从而导致坡面径流输沙特性发生异变，模型对训练样本的拟合误差较大。坡度为20°、30°时，坡面径流能坡较大，各观测断面的侵蚀形式主要为细沟侵蚀，模型对训练样本拟合较好。

4.2 模型验证与比较

使用训练所得GRNN_Adaboost 模型对测试样本的坡面径流输沙能力进行预测，结果见表5。

将GRNN_Adaboost 模型计算所得预测值与实测值进行对比分析，由图2 知:相关系数为0.983，表明预测值与实测值有较好的相关关系;决定系数R2为0.729，表明预测值与实测值之间存在很好的一一对应关系。

为检验GRNN 模型对坡面径流输沙能力的预测效果，使用广泛运用的BP(Back Propagation)神经网络进行对比验证，建立以6 个影响因子为输入、以坡面径流输沙能力为输出的3 层BP 神经网络模型，其隐含层神经元转移函数为

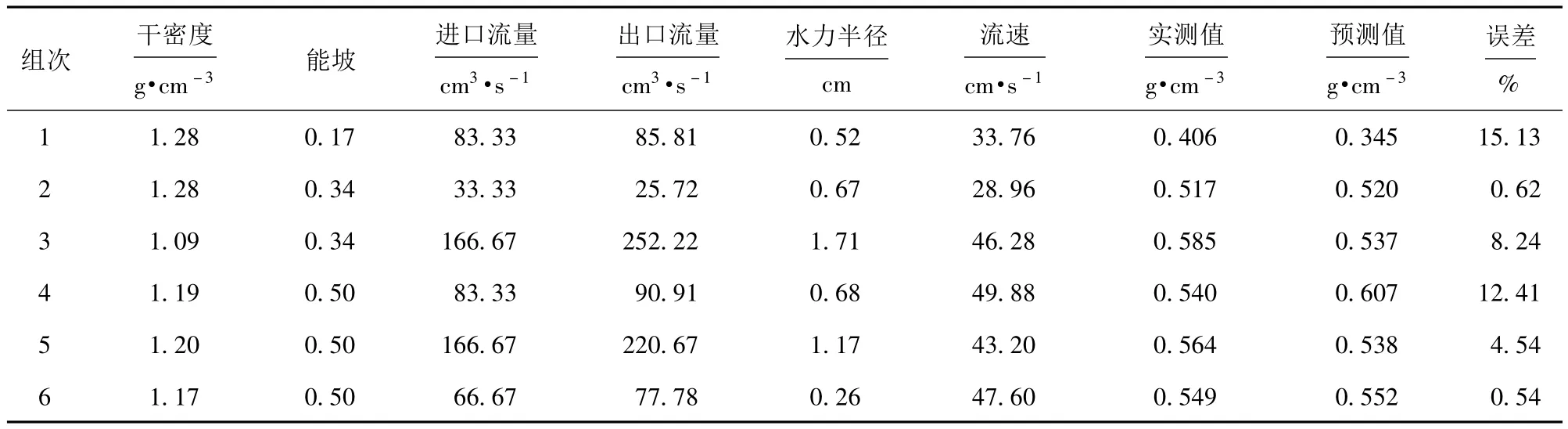
表5 GRNN_Adaboost 模型预测结果Tab.5 Predicted results of GRNN_Adaboost model

图2 坡面径流输沙能力预测值与实测值拟合关系图Fig.2 Fitting of measured values to predicted values of sediment transport capacity

将训练样本代入BP 神经网络模型进行训练，使用训练后的模型对测试样本的坡面径流输沙能力进行预测，并计算10 次预测结果与实测值的误差平均值。BP 神经网络、弱预测器GRNN、强预测器GRNN_Adaboost 在测试样本处的预测误差见图3。

图3 模型预测误差Fig.3 Prediction error of the models

由测试样本的模拟预测结果知:BP 神经网络模型的平均预测误差为18.40%。在坡度为10°的测试样本1 处取得最大预测误差30.05%，10 个GRNN 弱预测器的平均预测误差为13.20%;在坡度为10°的测试样本1 处取得最大预测误差22.49%，强预测器GRNN_Adaboost 的平均预测误差为6.91%;在坡度为10°的测试样本1 处取得最大预测误差15.13%。BP 神经网络、GRNN、GRNN_Adaboost 模型的测试样本平均预测误差依次较少，且均在坡度为10°的测试样本1 处取得最大预测误差，与模型的拟合情况一致。

由于网络拓扑结构、转移函数、学习速率和迭代次数等限制，BP 神经网络模型往往需要经大量训练样本多次迭代训练后才能较好地逼近测试样本。GRNN 的理论基础是非线性核回归分析，以样本数据为后验条件，执行Parzen 非参数估计，并依据概率最大原则计算网络输出。GRNN 最后收敛于样本量积聚较多的优化回归面，在训练样本较少时也能具有很好的网络泛化能力，取得较好的模拟预测结果。由于试验场次所限，可用训练样本数量较少，故选择GRNN 建立坡面径流输沙能力模型能够提高模拟预测的精度。Adaboost 算法根据训练所得弱预测器的预测误差不断调整样本权值，并将所有弱预测器按一定权重集成为强预测器，以提高模型的模拟预测精度。相对于弱预测器GRNN，强预测器GRNN_Adaboost 对测试样本的坡面径流输沙能力预测精度显著提高。

5 结论与讨论

1)根据试验资料的验证，GRNN 能够用于坡面径流输沙能力的预测。

2)使用MIV 方法分析了坡面径流输沙能力影响因子对GRNN 的影响，初步确定了建立GRNN 坡面径流输沙能力模型所需输入参量，即坡面土壤干密度、能坡，坡面流水力半径、流速，以及坡段的进口流量和出口流量。

3)Adaboost 算法能够有效提高GRNN 的预测精度，经该算法优化的GRNN_Adaboost 坡面径流输沙能力模型对测试样本的平均预测误差为6.91%，比GRNN 模型的平均预测误差减少了47.65%。

4)在试验训练样本条件下，BP 神经网络模型、GRNN 模型、GRNN_Adaboost 模型的模拟预测误差依次降低。

由于试验条件限制，本文未考虑不同粒径组成和坡长对坡面径流输沙能力的影响，不同试验条件下神经网络模型的类型选择问题也有待进一步研究。坡面径流输沙规律复杂，其预测难度较大，神经网络方法适用于此类复杂非线性问题的模拟预测，且无须对特定参数进行率定，具有使用简便、易于推广等特点。本文仅利用实体模型的试验资料对GRNN 预测方法进行了初步探讨。

［1］ Govers G，Rauws G.Transporting capacity of overland flow on plane and on irregular beds［J］.Earth Surface Processes and Landforms，1986，11:515－524

［2］ Everaert W.Empirical relations for the sediment transport capacity of interrill flow［J］.Earth Surface Processes and Landforms，1991，16:513－532

［3］ Abrahams A D，Li G，Krishnan C，et al.A sediment transpo rt equation for interrill overland flow on rough surfaces［J］.Earth Surface Processes and Landforms，2001，26:1443－1459

［4］ Cybenko G.Approximation by superpositions of sigmoidal function［J］.Mathematics of Control，Signals and Systems，1989，2(4):303－314

［5］ Hornik K，Stinchombe M，White H.Multilayer feedforward networks are universal approximators［J］.Neural Networks，1989，2(2):359－366

［6］ 陈雄波，唐洪武.用BP 神经网络原理对水流挟沙力的研究［J］.泥沙研究，2004(1):29－34

［7］ 熊建秋，李祚泳.基于支持向量机的水流挟沙力预测研究［J］.水利学报，2005，36(10):1171－1175

［8］ Chih T Y，Reza M，Mohammad T A.Evaluation of total load sediment transport formulas using ANN［J］.International Journal of Sediment Research，2009，24(3):274－286

［9］ Melesse A M，Ahmad S，McClain M E，et al.Suspended sediment load prediction of river systems: An artficial neural network approach［J］.Agricultural Water Management，2011，98(5):855－866

［10］张瑞瑾，谢鉴衡，王明甫，等.河流泥沙动力学［M］.北京:水利电力出版社，1989:204－230

［11］窦国仁，王国兵.黄河小浪底枢纽泥沙研究:报告汇编［R］.南京:南京水利科学研究院，1993:91－133

［12］张晴雯，雷廷武，高佩玲，等.黄土区细沟侵蚀过程中输沙能力确定的解析法［J］.中国农业科学，2004，37(5):699－703

［13］王少波，柴艳丽，梁醒培.神经网络学习样本点的选取方法比较［J］.郑州大学学报:工学版，2003，24(1):63－65

［14］Dombi G W，Nandi P，Saxe J M，et al.Prediction of rib fracture injury outcome by an artificial neural network［J］.The Journal of Trauma，1995，39(5):915－921

［15］Specht D F.A general regression neural network［J］.IEEE Transactions on Neural Network，1991，2(6):568－576

［16］Borra S，Ciaccio A D.Measuring the prediction error.A comparison of cross－validation，bootstrap and covariance penalty methods［J］.Computational Statistics＆Data Analysis，2010，54(12):2976－2989

［17］Freund Y，Schapire R E.A decision－theoretic generalization of on－Line Learning and an Application to Boosting［J］.Journal of Computer and System Sciences，1997，55(1):119－139

［18］Schapire R E，Singer Y.Improved boosting algorithms using confidence－rated predictions［J］.Machine Learning，1999，37(3):297－336

［19］肖培青，郑粉莉，汪晓勇，等.黄土坡面侵蚀方式演变与侵蚀产沙过程试验研究［J］.水土保持学报，2008，22(1):24－27