黄土丘陵沟壑区坡沟系统切沟侵蚀数值模拟

2012-01-02李斌兵肖培青余叔同

中国水土保持科学 2012年1期

李斌兵，肖培青，余叔同

(1.武警工程大学信息技术教研室，710086，西安;2.黄河水利科学研究院水利部黄河泥沙重点实验室，450003，郑州;3.西北农林科技大学黄土高原土壤侵蚀与旱地农业国家重点实验室，712100，陕西杨凌)

切沟侵蚀包括沟底下切、沟壁扩展、沟头溯源侵蚀及其相伴的输沙沉积等过程，侵蚀过程既受水力作用又受重力作用，既有必然性又有随机性，行为非常复杂，研究难度较大，相关的研究成果较少，切沟重力侵蚀试验和野外观测资料缺乏，对认识切沟侵蚀力学机制并对其侵蚀量进行预报非常困难。沟蚀侵蚀过程及预报的问题严重影响了流域侵蚀产沙预报的结果，成为制约其发展的“瓶颈”。在切沟侵蚀演变过程与侵蚀产沙研究中，由于自然裸露坡面或陡坡农地细沟侵蚀向浅沟和切沟演变是一个相对漫长的过程;因此很难观测到切沟形成和演化过程中某位置和某时刻的瞬时水力学参数和土壤剥离及沉积量，目前只能通过概化模型进行模拟。在切沟侵蚀水动力学机制研究中，国内外学者［1-8］对坡面侵蚀的动力学规律进行了大量的研究，目前国外几个代表性的模型在径流水力学基础方面还存在较大的差异。例如，WEPP 模型采用了径流剪切力，EUROSEM和LISEM 模型采用了单位水流功率，而GUEST 模型则采用了水流功率。剪切力、水流功率和单位水流功率间存在明显的差异，哪一个参数更能准确描述土壤侵蚀过程，仍需要进一步深入研究。国内坡面流水力特性试验研究多集中于细沟流研究，对于坡沟系统径流水力学特性的研究较少。王文龙等［4，7］采用室内人工模拟降雨试验的方法，初步探讨了坡沟系统各种侵蚀方式的水力特性及其开始发生侵蚀的动力临界条件。肖培青等［9］采用变坡度坡沟系统概化模型和人工模拟降雨试验相结合的方法，研究了坡沟系统水流水力学参数变化特征。但是目前切沟流水动力学过程研究的深度和广度还远不能满足黄土高原水土流失规律研究和数学模型建设的需要，大大制约了具有物理成因的水动力学模型的进展。在切沟形态研究中，许多学者［10-14］提出了包含野外动态监测、高精度GPS 测量、三维激光扫描和GIS 技术相结合的沟蚀演变过程研究方法，估算了切沟侵蚀的体积和侵蚀量，但没有给出基于物理过程的切沟侵蚀模型。

综上所述，国内外切沟侵蚀模型研究还处于起步阶段，面临着很多挑战，现有的模型还不能模拟局部土壤剥离和泥沙沉积量变化，因而不能反映切沟瞬时形态的特征与时空变化。笔者通过对切沟侵蚀过程和机制的实验与数值模拟研究，揭示在水力和重力复合作用下，切沟侵蚀下切和输沙沉积过程机制，建立切沟下切方程，进行数值模拟，在坡沟系统上进行了验证，以揭示切沟侵蚀过程机制，建立切沟侵蚀模型，推动侵蚀预报模型发展。

1 坡沟系统切沟侵蚀模拟

1.1 坡沟系统切沟侵蚀模型

在切沟由起初发育到进入稳定状态过程中，起始阶段发展变化最快，切沟的长度、深度、宽度、表面积和体积变化剧烈，远离稳定，随着切沟侵蚀过程的进行，切沟发育演变趋缓，直至稳定。其发展过程为:如果水流剪切力大于土壤临界剪切力，在表土层或沟的底部形成一个矩形沟道，随着降雨过程的持续进行，切沟沟头不断溯源侵蚀使其加长、沟槽不断下切使其沟槽加深、沟壁崩塌使其加宽，切沟逐步由切沟发育的早期向中期、后期演变，最终进入切沟发展的稳定期。切沟是具有地理空间的微地貌，在切沟发育演变过程中，切沟的各种特征不仅随时间变化，而且在其上、中、下游等不同的部位也有空间上的差异;因此，切沟发育过程是一个时空动态的演化过程，切沟下切和沟壁坍塌等发育的速度与水流速度、水流剪切力、水深、流量、水流含沙量、泥沙沉速、土壤质地与土壤可蚀性等诸多水沙及土壤参数相关。

质量守恒原理是水沙运动遵循的普遍规律。在相距为dx 的坡段，在dt 时距内输入和输出该坡段的沙量之差与该坡段内水流中携带的沙量变化量之和，必然等于dt 时距dx 距离内水流下伏土壤表面的净侵蚀或沉积量;因而，可基于质量平衡原理，建立切沟侵蚀输沙微分方程，描述不同时间点沿程侵蚀输沙量的时空动态变化，方程见式(1)。式(1)的左边定义了dx 坡段dt 时距内输入输出沙量变化量与水流携带沙量变化量之和，方程的右边则定义了该坡段该时距内的净侵蚀或沉积。

侵蚀输沙过程的推移，会影响沿沟长剥离量与沉积量的变化，因此，在侵蚀过程中，坡面局部的土壤剥离和泥沙沉积会引起局部坡度的瞬态改变。其原因是沟床随时间是非均匀侵蚀，在时段dt 内地表剥离或沉积的净泥沙量可用式(2)表示，即为切沟侵蚀下切方程，定义了沟底高程随着分离的土壤颗粒和沉积的泥沙量变化而变化的过程。

坡沟实验结果［9］表明，切沟底部土壤分离速率主要与水流有效剪切力成正比，见式(3)。

式(1)和(2)的初始条件是:

式中:A 为径流横截面面积，m2;Q 为清水流量，m3/s;x 为沿坡距离，m;t 为降雨时间，s;C 为平均的体积比含沙量，m3/m3;Sd为切沟底部土壤颗粒分离率，m/s;Z 为沟底的高度，m;w 为径流宽度，m;vf为泥沙颗粒在湍流下的沉降速度，m/s;ε 为土壤孔隙度，m3/m3;K 为土壤可蚀性系数，s/m;τ 为沟底剪切力，m2/s2;τcr为临界剪切力，m2/s2;h 为径流的水深，m;ρ 为水的密度，kg/m3;g 为重力加速度，m/s2;S 为水力坡度，m/m。

对于湍流中的泥沙沉降速度，一般小于在静止水中的速度，选择张瑞瑾［15］提出的泥沙沉降速度计算公式

式中:vf为泥沙沉降速度，m/s;ν 为黏滞系数，cm2/s;ds为泥沙粒径，mm;ρs为泥沙密度，kg/m3，通常(ρs－ρ)/ρ=1.65。

1.2 模型求解

根据产汇流方程［16-17］和切沟侵蚀模型，利用坡沟系统的DEM，按照时空变化进行推演计算，时间推演以次降雨开始时间为起点，降雨结束为终点，将时间划分为若干时刻，空间从坡沟径流源点开始沿每条径流线一直演算到坡沟出口，在每一时刻上遍历每一条径流的全部网格，求解出每一网格的流量Q(i，j)和泥沙含量C(i，j)。

式(1)中，C 为待求的，C 随时间t 和沿坡距离x 而变化，下式中用C(x，t) 表示C 的动态变化，用差分方法对其进行求解，首先用Δx 与Δt 分割(0，0)－(x，t)平面，见图1，x 为沿沟长的距离(m)，t 为降雨结束时间(s)，采用下列近似公式:

式中θ 为Pressmann 隐式差分格式中的权重系数。

将偏微分方程(1)离散为下列差分方程(6)，进而求解。

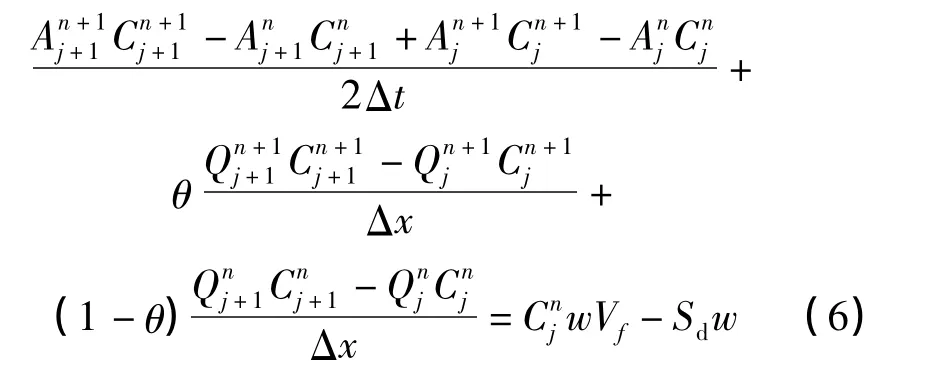
图1 径流-时间离散图Fig.1 Runoff-time discrete graph

式(2)求解过程为:

把方程(3)代入方程(2)得:

设a=Kgρh

因S 为坡度，即高程随位置的变化率，所以

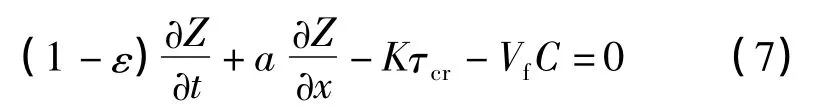
式(7)可以用Lax-Wendroff 显式方程求解，即用有限差分代替方程中的微分，再利用迭代算法求解。其推导过程为:

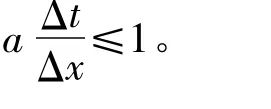
2 模拟结果与检验

文献［9］中给出了在安塞水土保持综合试验站实体模型上进行的模拟降雨实验结果，实体模型是根据黄土丘陵沟壑区坡沟空间分异特征和野外调查量化的典型坡沟系统的参数特征制作的，模型土槽高6.01 m、宽3.05 m、投影长12 m，投影面积40 m2，见图2。待降雨结束后，快速用LIDAR 三维激光扫描仪获取地面地形信息，将测量数据导入ArcGIS 平台进行处理，经过插值生成模拟降雨试验后的DEM，将切沟初始形成时刻(沟底开始出现下切)生成的DEM 作为切沟模型的起算DEM 数据，网格大小为20 cm，采用径向基插值方法生成DEM。降雨强度分别为0.83、1.66 和3.60 mm/min，土壤吸力参数sf取572.52 mm，土壤初始饱和含水率为0.155，饱和含水率为0.465，曼宁糙率系数n=0.108(s/m1/3)，饱和导水率Ks=0.010 07 mm/s，切沟出口处的径流量和侵蚀量观测计算方法见文献［16-17］。

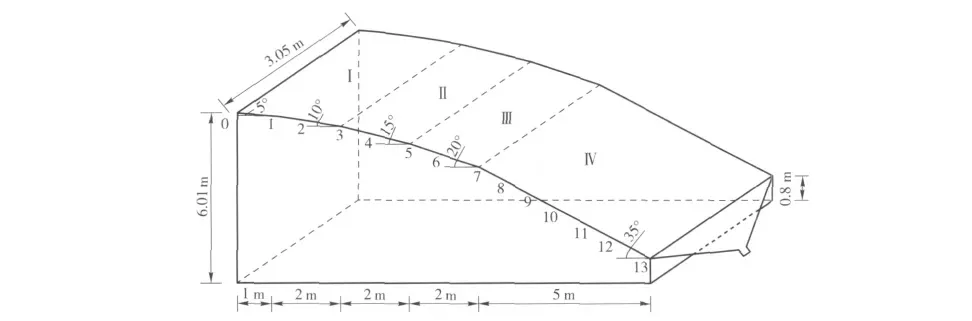
图2 坡沟系统实体模型示意图Fig.2 Schematic diagram of solid model of hillslope-gully system

不同降雨强度降雨试验中经测量得到的沟深度值与本文模型计算得到的模拟值见表1、2、3。0.83 mm/min 降雨强度降雨试验中沟深模拟值与实测值的相对误差基本上在±25%以内，1.66 mm/min 降雨强度降雨试验中，沟深模拟值与实测值相对误差基本上在±15%以内，3.60 mm/min 降雨强度降雨试验中，沟深模拟值与实测值相对误差基本上在±16%以内。大、中、小3 种降雨强度下的检验结果说明在不同降降雨强度度下采用本文模型计算出的沟深模拟值与实测值较接近。进一步分析沟深相对误差的分布可知坡面上部沟深模拟值相对误差较大，而在坡面下部相对误差较小，这是因为坡面上部沟蚀发育没有坡面下部剧烈，坡面上部雏形侵蚀沟的沟深较小，给测量精度带来影响，测量数据可能与实际值有所偏差。总的来说，采用本文切沟模型模拟能够反映沟蚀沟深的发育情况。

表1 0.83 mm/min 降雨强度沟深模拟相对误差Tab.1 Relative errors of simulated gully depth at 0.83 mm/min rainfall intensity

续表1

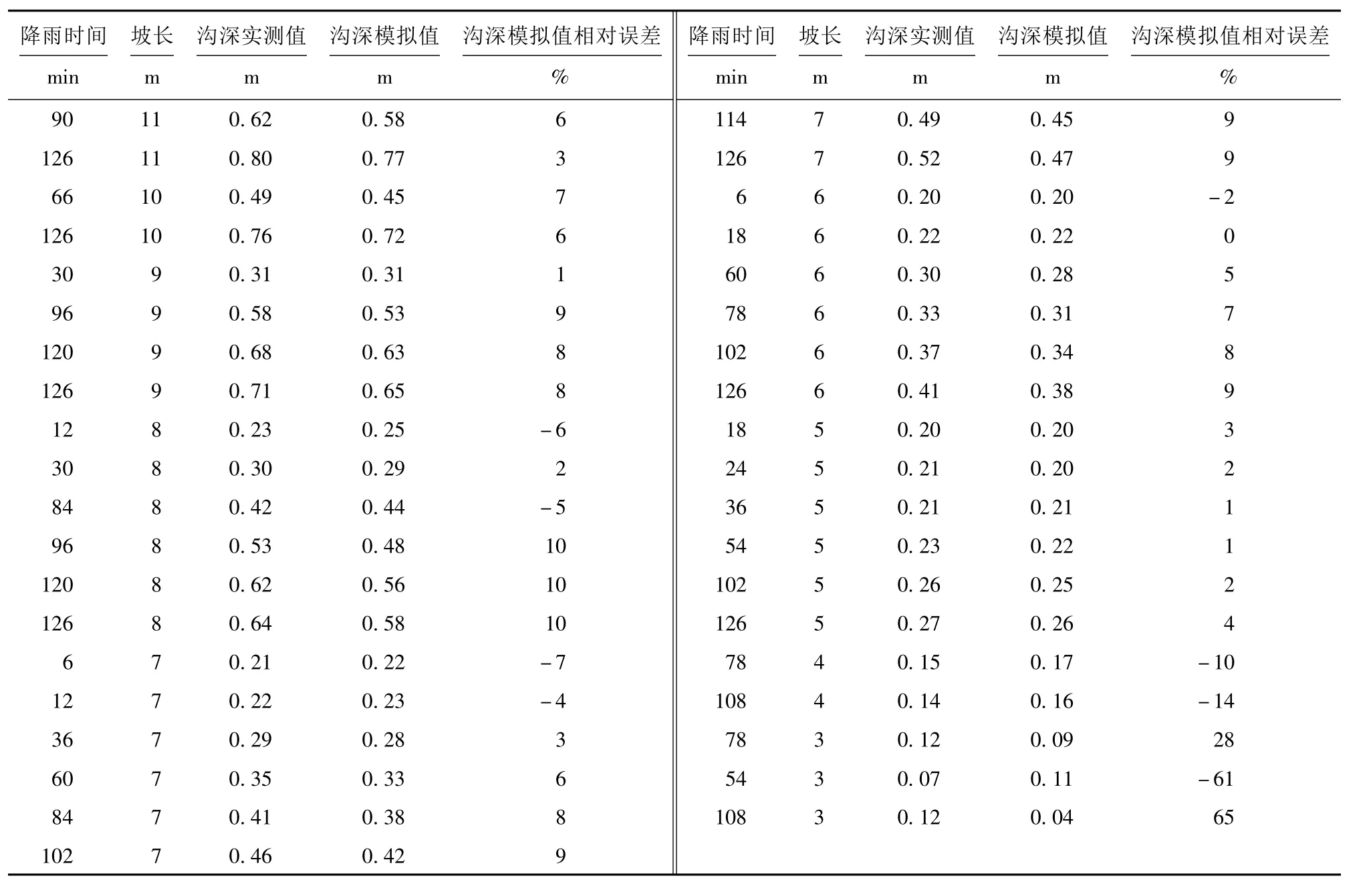
表2 1.66 mm/min 降雨强度下沟深模拟的相对误差Tab.2 Relative errors of simulated gully depth at 1.66 mm/min rainfall intensity

表3 3.60 mm/min 降雨强度下沟深模拟的相对误差Tab.3 Relative errors of simulated gully depth at 3.60 mm/min rainfall intensity

3 结论与讨论

1) 依据质量守恒原理，考虑了影响切沟水沙运动的各物理要素，建立了坡沟系统切沟侵蚀模型，给出了有限差分法的推导过程。将建立的切沟侵蚀模型与降雨入渗、产汇流模型进行耦合计算，利用迭代算法编写程序求解了不同时刻和不同坡长下的切沟深度数据。经过与试验观测结果比较检验，平均相对误差在15%以内，取得了较高的模拟精度。

2) 从模型计算与试验观测的比较结果看，坡面上部沟深模拟值相对误差较大，而在坡面下部相对误差较小。这是因为坡面下部相比上部，切沟侵蚀剧烈。总的来说，本文模型模拟能够反映切沟沟深的发育情况。

3) 尽管在坡沟系统下，动态切沟模型取得了较好的模拟效果，下一步拟开展在流域尺度下的验证和测试。其难度在于:切沟的空间尺度大，分布位置上地形多险峻，在我国黄土丘陵沟壑区地形则更是破碎，切沟侵蚀过程很复杂;因此，时至今日，国内外还没有布设过野外切沟侵蚀过程的水沙观测。因此，难以为模型验证提供必需的水流水力学参数和切沟形态演化数据。实体模型仍是目前有效的手段之一，研究具有严格比尺意义的实体模型，满足几何相似、降雨相似、水力相似等条件是建立小流域侵蚀模型的基础和重要工作。

［1］ Nearing M A，Norton L D，Bulgakav G A，et al.Hydraulics and erosion in eroding rills［J］.Water Resources Research，1997，33(4):865-876

［2］ Foster G R，Huggins L F，Meyer L D.A laboratory study of rill hydraulics:I.velocity relationship［J］.Trans of ASAE，1984，27(3):790-796

［3］张科利，唐克丽.黄土坡面细沟侵蚀能力的水动力学试验研究［J］.土壤学报，2000，37(1):9-15

［4］王文龙，雷阿林，李占斌.土壤侵蚀链内细沟浅沟切沟动力机制研究［J］.水科学进展，2003，14(4):471-475

［5］丁文峰，李占斌，鲁克新，等.坡面细沟发生临界水动力条件初探［J］.土壤学报，2003，40(6):822-828

［6］张光辉，刘宝元，何小武.黄土区原状土壤分离过程的水动力学机理研究［J］.水土保持学报，2005，19(4):48-52

［7］王文龙，王兆印，雷阿林，等.黄土丘陵沟壑区坡沟系统不同侵蚀方式的水力特性初步研究［J］.中国水土保持科学，2007，5(2):11-17

［8］李占斌，秦百顺，亢伟，等.陡坡面发育的细沟水动力学特性室内试验研究［J］.农业工程学报，2008，24(6):64-68

［9］肖培青，郑粉莉，姚文艺.坡沟系统坡面径流流态及水力学参数特征研究［J］.水科学进展，2009，20(2):236-240

［10］伍永秋，刘宝元.切沟、切沟侵蚀与预报［J］.应用基础与工程科学学报，2000，8(2):134-142.

［11］胡刚，伍永秋，刘宝元，等.GPS 和GIS 进行短期沟蚀研究初探:以东北漫川漫岗黑土区为例［J］.水土保持学报，2004，18(4):16-19.

［12］游智敏，伍永秋，刘宝元.利用GPS 进行切沟侵蚀监测研究［J］.水土保持学报，2004，18(5):91-94