单脉冲测角在BM突防干扰机上的应用*

陈方予，崔晓东，吴建军，郝昀

(1．北京机电工程总体设计部，北京 100854;2．江苏省教育考试院，江苏南京 210024)

0 引言

弹道导弹(ballistic missile，BM)弹头突防时，常使用伴随式突防干扰机产生多假目标信号，干扰反导雷达对进攻弹头的探测。

随着雷达探测能力的提高，宽带高分辨雷达(high-resolution radar，HRR)检测接收信号的HRRP(high-resolution radar range profile)特性［1］，利用回波信号的HRRP特征鉴别回波信号性质。

先进的反弹道导弹(anti-ballistic missile，ABM)系统常使用宽带HRR，用以识别在HRRP上与真弹头回波信号不一致的末修舱回波信号、发动机碎片回波信号、电子点假目标信号和球形诱饵回波信号等非弹头回波信号［2］。由此要求BM突防干扰机能够针对HRR反导雷达产生具有与BM弹头回波信号一致的HRRP特征的多假目标信号。

BM突防干扰机生成包含BM弹头HRRP特征的假目标信号时，需要知道探测雷达观测BM弹头的观测角，进而确定BM弹头HRRP的长度、前点徙动范围和多普勒调制等 HRRP参数［3－4］。

雷达观测角的测量可使用电子无源测向系统进行测量［5－8］，其中包括使用无源单脉冲测角系统［9］。

当BM突防干扰机与BM弹头有相同的攻角，即相对探测雷达有相同姿态角时，此时如果BM突防干扰机能够使用无源单脉冲测向系统测出探测雷达的照射角，则测得的雷达照射角与雷达探测BM弹头的观测角有对应关系，干扰机可据此得到BM弹头HRRP的长度。

BM突防干扰机使用时由突防干扰装置在空中释放。释放时，释放装置将对干扰机进行授姿和运动参数加载(包括释放方向、释放姿态、分离速度、旋转速度等)。

用于稳定空间飞行器姿态的三维姿态稳控系统通常有较大的体积和质量(如BM使用的三维惯组和姿态修正系统)，难以在BM突防干扰机上应用。BM突防干扰机通常自身没有姿态测量、姿态调整和姿态稳控装置。释放时，为防止因释放力不均和后续可能受到扰动而引起的干扰机整体侧滚，干扰机采用慢速自旋方式与释放装置分离，将因释放力不均和后续可能受到的扰动产生的测向转动能量转化为章动能量，维持自身姿态角的基本稳定。

无源测向系统测得的雷达到达角(angle of arrival，AOA)是相对测量平台的。自旋转动下的BM突防干扰机若使用二维无源单脉冲测向系统测量雷达AOA，因测量平台随干扰机自旋转动，此时虽能实时测量雷达AOA，但因干扰机不能实时确定自身测量坐标系与雷达观测平面之间的关系，测得的雷达AOA难以与雷达观测角对应起来，因此在缺少姿态测量装置情况下，自旋转动的BM突防干扰机使用二维无源单脉冲测向系统测量雷达观测角将受到干扰机自旋转动的限制。

注意到BM突防干扰机自旋转动的特点，若使用一维无源单脉冲测角系统测量雷达AOA，测得的雷达AOA将随干扰机自旋呈周期性变化，如果在BM突防干扰机一个自旋周期内测得的雷达AOA数据变化是单调的且有稳定的最大值和最小值，同时最大值或者最小值能够与雷达观测角对应起来，那么这样干扰机就能够实现对雷达观测角的测量，下面探讨这种方法的可行性。

1 旋转一维无源单脉冲测角系统测量雷达观测角

1．1 旋转一维无源比相单脉冲测角系统测量雷达观测角

假定BM突防干扰机与进攻的BM弹头有相同的攻角，即两者相对探测雷达有相同的姿态角，这是BM突防干扰机能够测量雷达观测角的前提。如果不能保证BM突防干扰机与BM弹头相对探测雷达有相同的姿态角，那么干扰机测得的雷达AOA与雷达观测BM弹头的观测角之间将可能没有相对明确或者稳定的关系，测得的雷达AOA对模拟BM弹头HRRP也就可能难以提供准确的雷达观测角参数。

实际中，BM弹头具有调姿和稳控装置(包括自旋)，可通过调姿和稳控装置调整和稳定自身姿态。BM突防干扰机目前虽然较难具备空间二次自定姿能力，但通过释放装置释放时的授姿和自旋转动也可以取得和稳定自身的飞行姿态，工程上，通过合理的设计可以实现两者相对探测雷达有基本一致的姿态角。

BM突防干扰机可采用一维无源比相单脉冲测角系统(干涉仪)测量雷达 AOA［10－11］。图 1示意了干扰机测角基准轴AB，BM弹头和观测雷达三者间的相对位置关系。

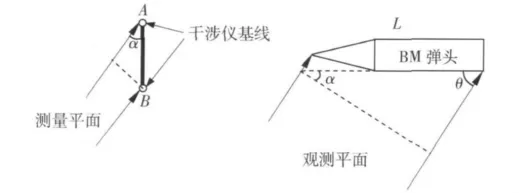
图1 干扰机测角基准轴AB，BM弹头和观测雷达间相对位置关系Fig．1 Relation among jammer’s angle measure benchmark axis，BM warhead and detecting radar

雷达观测BM弹头时，左右两端视线与弹轴构成观测平面，设观测视线与弹轴夹角为θ，BM弹头长度为L，则BM弹头在雷达观测方向上的投影长度为Lcos θ，这个长度是BM突防干扰机生成BM弹头回波信号中HRRP特征时需要的参数。

雷达观测角θ只与BM弹轴(或干扰机轴)与雷达观测视线间的夹角有关，与两者具体相对位置无关，只要求出θ值，可不必关心θ角的具体方向。

图1中，测角基准轴AB随干扰机自旋在与纸面垂直的平面内以AB轴中点为中心旋转。AB轴和雷达照射线构成测量平面，测得相对AB轴的雷达AOA为α。由于AB轴随干扰机自旋转动，测得的雷达AOA数值将随干扰机自旋呈周期性变化。

如图1所示，当干扰机测量雷达AOA的测量平面与雷达观测BM弹头的观测平面共面时，α与θ互余，即α+θ=π/2。据此:若能根据一维干涉仪测角基准轴转动的特点提取出干扰机测量雷达AOA的测量平面与雷达观测BM弹头的观测平面共面时的雷达AOA，就可得到雷达观测BM弹头的观测角θ，下面探讨其可行性。

旋转的一维干涉仪测角系统与探测雷达之间的几何关系如图2所示。

设:探测雷达位于P点位置;干涉仪测角基准轴AB以O点为圆心逆时针转动;PQ为P点到AB旋转面的垂线，干扰机轴线为 OO'，PA=x，PO=d，AO=r。

△ABP构成干扰机测量雷达AOA的测量平面。

△POO'构成雷达观测BM干扰机(BM弹头)的观测平面。

图2 旋转一维干涉仪测量雷达AOAFig．2 Revolving one-dimension interferometer measure radar AOA

因为 PQ∥OO'，所以 P，Q，O，O'4 点共面，即PQ在观测平面内。

在△AOP中，根据余弦定理有

注意到实际上 x≫r，因此 cos α'x＞0，即cos α↗。对应0～π间的α，α↘，即α随x单调递增而递减。

AB转向A'B'期间，QA'单调递减，PQ不变，x单调递减，cos α单调递减，α单调递增，转至A'B'时，α递增至接近π/2。AB转过A'B'继续转向BA期间，x仍然单调递减，α仍然单调递增，α递增至接近πα，取得最大值。当AB转过BA位置，继续向AB转动时，x单调递增，α单调递减，α向最小值靠近。

设测角基准轴AB与OQ共线时测角系统测得的雷达AOA为α0，当AB轴转至A'B'位置时，设转角为β。经计算，得到测角基线在A'B'位置时测得的雷达 AOA(α)满足关系式:cos α =cos α0cos β。图3给出了α0=π/3，β在0～π之间变化时对应的α仿真计算值。

图3 α0=π/3，β=0～π，α仿真计算值Fig．3 α simulation value while α0=π/3，β =0～π

由此可见，当测角基准轴AB与OQ共线时，即AB的延长线过Q点时，干涉仪测得的雷达AOA(α0)最小。

△ABP为测量平面，△POQ为观测平面，AB与OQ共线时，测量平面与观测平面重合，此时测得的雷达AOA值最小，这个最小值α与雷达观测BM干扰机(BM弹头)的观测角θ互余。

由上讨论可以看到，当一维干涉仪测角基准轴随干扰机转动一圈后，测得的雷达AOA最小值的余角就是雷达观测BM干扰机(BM弹头)的观测角θ。

一维干涉仪测角系统设计时，可使用双平衡混频器构成鉴相器，鉴相器可只鉴出PA，PB路径引入的到达波相位差，无需分清两路信号相位的相对前后关系，因此干涉仪测角基准轴只要转动半圈就可以得到雷达AOA的最小值。

为避免出现测角模糊，BM突防干扰机应采用短基线干涉仪测角系统，即A，B两天线间的距离需小于探测雷达信号波长的1/2。当BM突防干扰机前端结构允许时，可适当考虑增加一个相距较远一点的第3个天线，以提高测角精度。

1．2 旋转一维无源比幅单脉冲测角系统测量雷达观测角

BM突防干扰机可采用一维无源比幅单脉冲测角系统测量雷达AOA［10－11］。图4示意了干扰机测角差波束、BM弹头和探测雷达三者间相对位置关系。

图4 干扰机测角差波束、BM弹头和探测雷达间相对位置关系Fig．4 Relation among jammer’s angle measure difference beam，BM warhead and detecting radar

一维比幅单脉冲测角系统中测角天线两个差波束电轴构成测量雷达AOA的测量平面，测量平面随干扰机自旋而旋转。

根据比幅单脉冲测角原理和立体几何关系，采用如上分析方法，可以得到:当测量平面旋转到与雷达观测平面共面位置时，比幅单脉冲测角系统给出雷达AOA最大值，这个最大值等于雷达观测BM干扰机(BM弹头)的观测角θ。

由上可见，BM突防干扰机使用一维无源单脉冲测角系统(包括比相单脉冲和比幅单脉冲测角系统)，根据测角系统旋转的特点，在干扰机自旋半周时间内能够得到雷达AOA的最大值和最小值，同时得到的雷达AOA最大值或者最小值与雷达观测BM弹头(BM干扰机)的观测角有直接对应关系，据此可得到雷达观测BM弹头的观测角。

BM突防干扰机使用一维无源单脉冲测角系统，通过测量雷达AOA，可得到雷达观测BM弹头的观测角，然后根据事先已知的弹头长度L即可算出弹头HRRP的长度，再根据弹头几何和材料不连续点位置、弹头质心位置、章动角、锥旋速度等参数，计算出需要模拟的弹头HRRP中强散射点个数、位置，前点徙动速度和范围、多普勒调制等HRRP特征，生成多个包含BM弹头HRRP特征的回波信号，干扰制导雷达对进攻弹头的检测。

2 工程意义

BM突防干扰机使用一维无源单脉冲测角系统测量雷达AOA时，由于干扰机自旋，测得的雷达AOA数值呈周期性变化，其中最大值和最小值是需要的参数，但最大值和最小值得到的时间呈间断的周期性。

实际中，BM弹头和BM突防干扰机相对探测雷达是运动的，干扰机需要实时生成包含BM弹头HRRP特征的信号发送给探测雷达。注意到BM突防干扰机得到的雷达观测角是不连续的，具有步进离散性，因此干扰机发送给探测雷达的假目标信号HRRP长度是步进离散的，但如果这种具有步进离散长度的HRRP信号对模拟BM弹头HRRP特征影响不大，能够基本满足要求，那么这种做法还是有一定工程意义的。

BM突防干扰机使用一维无源比相单脉冲测角系统时，由于BM突防干扰机体积受限，不易使用长基线测角系统，易使用短基线测角系统。短基线测角系统的测角精度比长基线测角系统低，与比幅单脉冲测角系统相近，设其为6°。

假设BM突防干扰机自旋速度为2 rad/s，雷达探测脉冲周期为1 ms。

干扰机自旋转动1/2 rad需时间0．25 s。0.25 s时间内干扰机测得的雷达AOA信号数量为250个。在1/2 rad(对应最大180°)角域内，测角系统可达到的角分辨力为 180°/250=0．72°，小于测角系统精度6°，BM突防干扰机自旋对测量雷达观测角影响较小。

假设BM突防干扰机和BM弹头飞行速度马赫数为5，0．25 s时间内干扰机和弹头飞行直线距离为412 m，若BM弹头和BM突防干扰机距反导雷达距离为100 km，如图5所示。则412 m横向移动距离引起的观测角变化量Δα=(412 m/100 km)×(180/π)=0．23°，对模拟 BM 弹头 HHRP 长度影响较小。

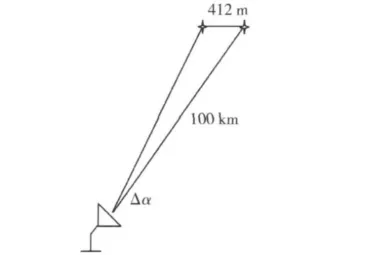
图5 干扰机移动对模拟BM弹头HRRP影响Fig．5 Effect jammer moving on simulating BM warhead HRRP

设BM突防干扰机的章动角为15°左右，单脉冲测角系统的测量精度和干扰机自旋产生的测角误差均比章动角小，对干扰机测量雷达观测角影响不大。影响测量雷达观测角精度的主要因素是干扰机的章动，因为干扰机的章动将引起测角天线旋转平面的倾斜，干扰机天线旋转平面倾斜将使得干扰机测得的雷达观测角与雷达实际观测BM弹头的观测角之间存在误差，对一些不采用自旋稳控的BM弹头，如果BM弹头章动角小，而BM突防干扰机章动角过大，则干扰机测得的雷达观测角可能呈现较大起伏，进而需要对测量数据作平滑处理，干扰机章动周期大于自旋周期，数据平滑处理需要时间，这样可能会影响干扰信号的实时性，应尽可能地减小干扰机的章动角。

实际中，在BM弹道中段，BM弹头和BM突防干扰机距反导雷达较远(如100 km)，在一个雷达观测角提取时间内(如0．25 s)，因BM弹头和BM突防干扰运动产生的雷达观测角变化较小，对BM突防干扰机生成BM弹头HRRP长度影响较小。

由上可见，BM突防干扰机根据自身自旋特点，使用一维无源单脉冲测角系统测量反导雷达观测角，进而确定BM弹头HRRP长度，这种做法目前理论上是可行的，且有一定的实际工程意义。

3 结束语

BM突防干扰机根据自身自旋的特点可使用一维单脉冲测角系统测量反导雷达观测角。这种方法有效的前提是BM突防干扰机和BM弹头相对探测雷达有基本一致的姿态角，而若使两者相对探测雷达有基本一致的姿态角，则需要干扰机释放时释放装置对干扰机有正确的授姿(包括释放角度、释放速度和起旋速度等)，同时干扰机通过自旋稳定姿态角时应有比较小的章动角。小的干扰机章动角可提高干扰机测量雷达观测角的准确度。减小干扰机章动角的方法除释放干扰机时尽量减小释放力的不均匀性，尽量做到平稳释放外，还可适当提高干扰机的自旋速度。干扰机自旋速度增加，在相同侧滚能量下，干扰机的章动角会相对小些［12］，另外，提高干扰机自旋速度还可缩短提取雷达观测角时间，增强干扰信号的实时性。

综上所述，虽然目前BM突防干扰机使用一维无源单脉冲测角系统测量反导雷达观测角有要求BM弹头与BM突防干扰机有基本一致的姿态角以及干扰机章动影响雷达观测角测量结果的缺点，但从工程上来看，这种方法目前还是具有一定实际意义的。

［1］ Donald R Wehner．High-Resolution Radar［M］．Second Edition．London:Artech House Boston，1995．

［2］ 李宝柱，袁起，何佩锟，等．一种利用宽带信号对弹道目标成像和跟踪的方法［J］．系统工程与电子技术，2009，31，(7):1588－1591．

［3］ 袁莉，陶巍．弹道导弹目标的距离像特征与特性分析［J］．制导与引信:目标特性专刊，2009，30(2):7－10．

［4］ 陈方予，崔晓东，李明，等．BM弹头雷达一维像干扰初探［J］．现代防御技术，2011，39(1):145－151．

［5］ 孙仲康，周一宇，何黎星．单多基地有源无源定位技术［M］．北京:国防工业出版社，1996．

［6］ 董志荣．单站单目标被动定位与跟踪的数学理论［J］．舰船科学技术，1996，(4):17－27．

［7］ 郭福成，孙仲康．方向角及其变化率的单站无源定位的可观测性［J］．系统工程与电子技术，2002，24(9):30－32．

［8］ 何友，关欣，衣晓．纯方位二维运动目标的不可观测性问题研究［J］．系统工程与电子技术，2003，25(1):11－14．

［9］ 司锡才，赵建民．宽频带反辐射导弹导引头技术基础［M］．哈尔滨:哈尔滨工程大学出版社，1996．

［10］ Merrill I Skolnik．雷达手册［M］．王军，林强，米慈中，等，译．北京:电子工业出版社，2003．

［11］ 丁鹭飞，耿富录．雷达原理［M］．3版．西安:西安电子科技大学出版社，2002．

［12］ 屠善澄．卫星姿态动力学与控制:第1卷［M］．北京:中国宇航出版社，1999．