基于CUBE算法的多波束测深数据自动处理研究

王海栋，柴洪洲

（1．信息工程大学 测绘学院，河南 郑州 450052；2．海军出版社，天津 300450；3．海军海洋测绘研究所，天津 300061）

基于CUBE算法的多波束测深数据自动处理研究

王海栋1,2，柴洪洲1,3

（1．信息工程大学 测绘学院，河南 郑州 450052；2．海军出版社，天津 300450；3．海军海洋测绘研究所，天津 300061）

对CUBE算法自动处理多波束测深数据的模型建立、格网节点的多重估计和最优估值选取准则进行了详细介绍，深入分析了多重估计的实用性，并通过实测数据对该算法进行实现。利用了抗差Kalman滤波改进CUBE算法。通过模拟数据对改进的CUBE算法进行实验，验证了算法改进的必要性。

多波束测深；CUBE算法；抗差估计；Kalman滤波；异常值检测；规则格网

近年来，多波束测深系统测得的数据密度明显提高，这对精确绘制海底地形具有十分重要的意义，但同时也给数据处理带来了许多问题[1]。针对多波束数据异常值检测和海底地形格网估计的复杂性，美国新罕布什尔大学的B.R.Calder和L.A.Mayer[2]提出了一种自动处理多波束数据的CUBE（Combined Uncertainty and Bathymetry Estimator）算法。该算法通过建立贝叶斯动态线性模型BDLM（Bayesian Dynamic Linear Model），利用Kalman滤波和多重估计，并结合测深数据的水平和垂向不确定度来计算格网节点，具有良好的数据处理效果。

实质上，结合异常值检测的海底地形网格化思想国外已应用于多波束测深数据的处理中，而且用地形格网代替测深值作为水深的存档数据[3]。CUBE算法正是针对该工序提出的，算法具有高效性、客观性、稳健性及高精度等特点，已集成于许多商业软件[4]中，被广泛应用，但国内研究较少。本文主要针对该算法的理论实现与改进方法进行了研究。

CUBE算法通过计算每个测深点的水平和垂向不确定度，利用信息传播模型，将测深信息进行传递。在所测区域，利用估计节点及其联合精度来表示该区域水深。当测深值可用时，节点就接收该点信息并估计水深，进一步通过收集更多的数据进行及时更新。

1 CUBE算法模型的建立

为反映各水深值在节点的估值，综合考虑节点和测深点间距、水平和垂向测量精度，建立测深点i对节点j的预报信息模型为：

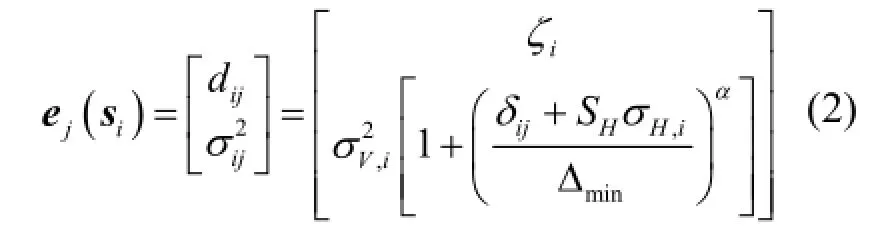
由于只预报格网节点的水深，而且格网间距设置较小，因此可将节点估值假定为一个常量，通过贝叶斯动态模型理论处理序列化的测深值，考虑最简单的常均值模型[7]：

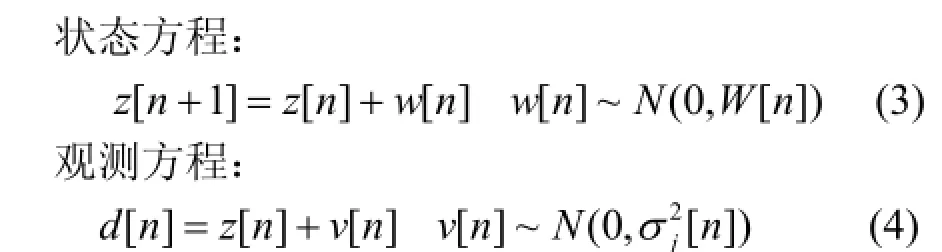
式中，z[n]为节点水深估值，d[n]为测深值，为服从方差为的零均值高斯白噪声，为系统状态噪声，表示模型的可信程度，并假定其方差W[n]为常值0[2]。该模型也是离散线性系统模型[8]的简化，作为CUBE算法的Kalman滤波模型。利用该模型计算，只保留当前的水深估值，待新数据进入后进行更新，减小了计算过程的存储。

2 CUBE算法的格网节点估计

为保证输入测深值的初始数据不为异常值，利用中值滤波对数据序列进行排序，按照靠近中位数的情况将输入数据序列的可信值前移，将异常值延后，再利用Kalman滤波对排序后的数据进行迭代，计算节点估值。

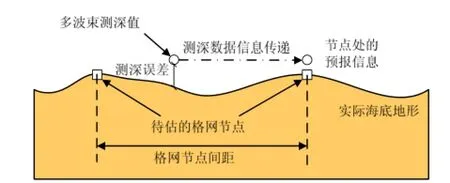
图 1 测深点在节点处的信息预报Fig.1 Prediction information from sounding to node

如图1为测深点对格网节点的信息预报示意图，运用Kalman滤波给出了状态参数的递推公式作为格网节点估值，将测深点的信息传递给格网节点，由于算法主要对格网节点进行估计，因此计算过程简化了滤波的状态方程。

3 多重估计及最优估值选取准则

在格网节点的估计过程中，输入数据常含有一定量的测深异常。若将其和正常值分别进行估计，得到节点的多个估值，利用最优估值选取准则对其作进一步判断，可提高结果的可信度。

3.1 算法的多重估计及其实现

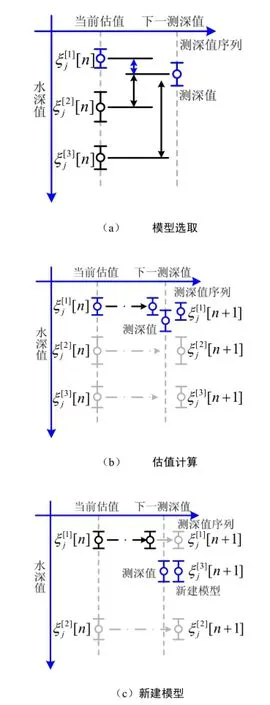
图 2 多重估计及最有效模型选取Fig.2 Multiple estimations and available model selection

利用存在跳变的测深数据序列进行多重估计的实现，结果如图3所示，该图同时比较了多重估值与单个估值的计算结果。从图中可见，当测深数据存在明显跳变时，节点的多重估值未被跳开的测深数据破坏，当380个测深点附近的连续异常数据消失时，估计又继续连接第一个估值，而单个估值的计算未正确估计节点水深。

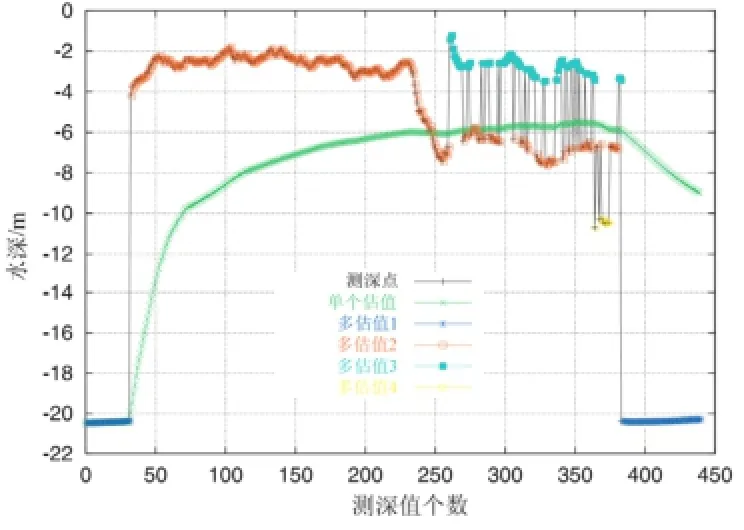
图 3 多重估值与单个估值的实验结果比较Fig.3 Comparison of multiple estimates with single one

由此可见，当存在连续异常的情况下，对节点做多重估计要明显好于单个估值的计算，多重估计是将不一致的测深数据得到各自内部一致的估值，这在一定程度上使算法具有稳健性。

3.2 最优估值选取准则

通过以上的步骤，每一个节点都能够得到相应的节点估计信息，其包括水深估值、验后方差以及估值的数量。当节点具有多重估值时，利用最优估值选取准则来确定最优估值的序号k，使同时将其他估值对应的测深点检测为异常值。

最简单的准则是通过用于估计的测深点数量来确定k值，公式如下：

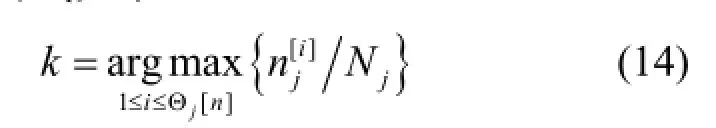
一般情况下，上式在选定估值时速度较快而且准确性较高，然而，在有连续脉冲状异常时，有可能使异常值的数量比正常数据高，这一准则可能不适用，顾及海底曲面的连续性，节点j的水深和其邻近节点应接近，因此，可利用局部区域水深信息的相关性来确定k值。

可依据处理时间的要求和数据的复杂程度选择以上3种方法之一进行判断。

格网节点多重估计使算法合理地处理了测深数据异常值的问题，但也说明具有多重估值的节点周围存在测深异常，因此，实际处理多波束数据时，需对这些区域的处理结果进行审核。

4 基于抗差估计的CUBE算法改进

由于每个多重估计模型内部，CUBE算法假设测深数据服从正态分布。但当测深数据所含的异常值偏离程度较小，不足以建立多重估计时，模型内部的数据分布受到污染，Kalman滤波估计节点的精度下降，虽然程度较小，但若要建立高精度的海底地形，还是不可忽视的。因此，提出利用抗差Kalman滤波对该情况下的CUBE算法进行改进。

抗差Kalman滤波常用于对动态系统含有异常的观测值进行估计[10]，来弥补Kalman滤波对污染分布数据处理的不足。假设测深值相互独立，并可能含有异常，且服从污染正态分布：

一步预测方差：

利用滤波获得测深值残差，并通过权函数确定其对应的等价权，再次对数据进行滤波，各测深值第m步抗差迭代组成的方差阵与等价权阵的关系为，等价权值可利用IGGⅢ方案确定[11]，计算中可将0等价权对应的测深值标定为异常。

5 CUBE算法及其改进方法的实现

实验的测深数据来自NOAA测量船在2001年测得的美国新罕布什尔州Portsmouth市入海口数据，使用SeaBat 8101多波束测深仪，已做声速剖面、潮汐等改正。

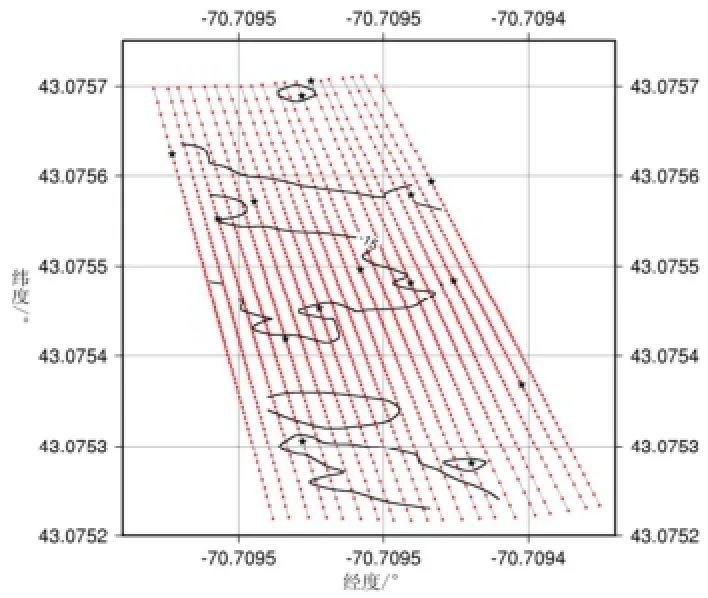
图 4 测深数据分布图Fig.4 Bathymetry data distribution

取20个无异常值的扇区，由于通常情况下边缘波束质量较差，所以舍弃条带两边各10个波束，并对数据加入15个异常值。波束点和异常值的分布如图4所示，星形点为测深异常位置，将数据进行CUBE算法编程实现。格网间距取0.7 m，共有节点949个，计算结果如图5所示。算法在得到海底地形规则格网图之前，会得到格网多重估值个数的情况，如图5(a)。比较图4和图5(a)可以发现，估值个数在2个以上的区域同时也存在测深异常。

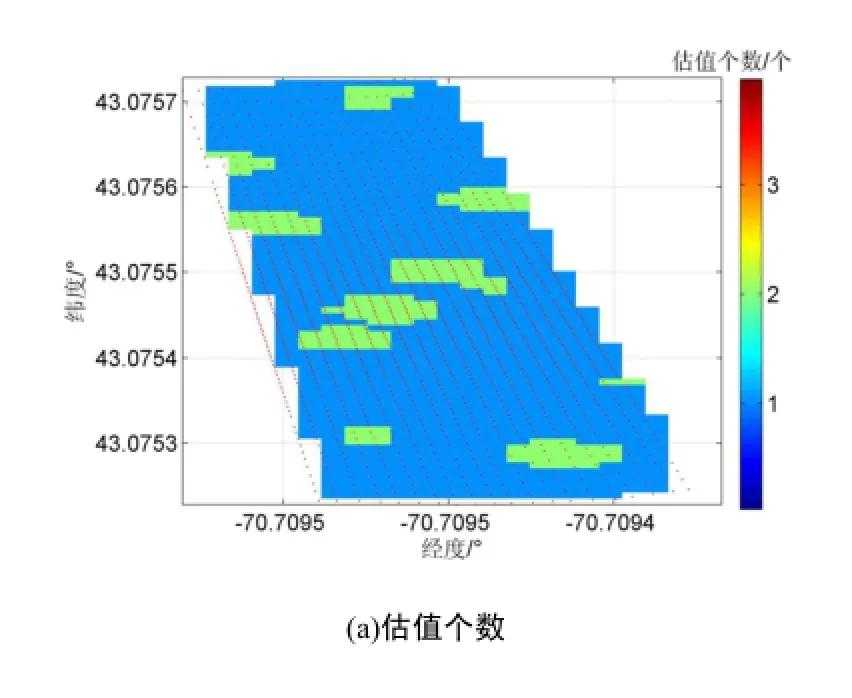
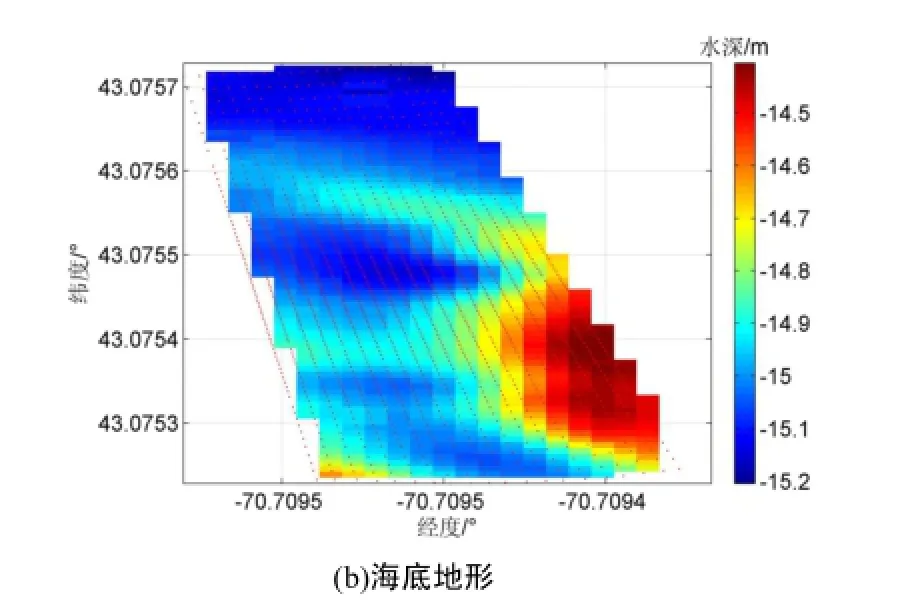
图 5 CUBE算法计算结果Fig.5 Results of CUBE algorithm

实验利用式(16)准则进行最优估值的选取，获得图5(b)所示的海底地形规则格网图，其准确反映了海底的地形情况。

对改进方法实验，模拟95个水深为20.5 m，精度为0.05 m的测深数据，并加入3个残差为0.2 m的异常值，用于估计一个节点（图6(a)）。为说明改进算法的优点，分别通过以下两种方案进行计算：

方案1：利用原CUBE算法进行多重估值计算；

方案2：基于抗差Kalman滤波的CUBE算法进行节点估计。

由于方案2用到IGGⅢ权函数，而滤波过程中，方差为等价权的倒数，因此在实际计算过程中，将权函数等于0的值用一小正数代替。

两方案的计算结果如图6(a)所示，从图中可见，所加入的异常值由于偏离程度较小，并未使CUBE算法建立多重估计。但计算过程中，方案1的滤波过程受到了异常值的影响，致使节点估值在异常值处有较大的变化，而方案2未受到影响，估计比较稳定，抗干扰能力较好。滤波过程中两种方案水深估值的差值如图6(b)所示，实际测量过程中，由于仪器的测量精度不同，该差值可能进一步放大。因此，CUBE算法的改进是有必要的。另外，CUBE算法具体可通过CARIS软件实现，操作过程可参见文献[4]和[12]，本文不再赘述。

6 结 论

本文研究了CUBE算法的模型建立、格网节点估计以及多重估计的思想。该算法有效解决了自动处理的可靠性、稳健性及海道测量的安全性等问题，利用其估计的规则格网容易生成海底三维地形图，人工处理时只需少量工作，提高了多波束处理的效率。

图 6 两种方案计算结果及比较Fig.6 Results and comparison of two schemes

在多个可信水深估值存在的区域，算法根据自定义的准则或人工方式选择最佳估值，是自动选择和人工判断最优水深的结合。

CUBE算法是个相对开放的算法，本文提出利用抗差Kalman滤波代替该算法中的Kalman滤波，减弱了较小异常对估值的影响，改进了该算法，进一步提高了格网节点估计的精度。也可以在其他方面改进，包括Kalman滤波模型的状态方程和观测方程，多重估值的选择准则等。

[1]李家彪, 王小波, 华祖根, 等.多波束勘测原理技术与方法 [M].北京: 海洋出版社, 1999.

[2]Calder B, Mayer L A.Automatic processing of high-rate, highdensity multibeam echosounder data [J].Geochem.Geophys.Geosyst , 2003, 4(6): 24-48.

[3]Armstrong A, Brennan R, Smith S.Implications of the Navigation Surface Approach for Archiving and Charting Shallow Survey Data [C].Shallow Survey 2003.Sydney Australia: 2003.

[4]CARIS.HIPS and SIPS 6.1.1 User’s Guide [M].Fredericton, NB: Universal System Ltdp, 2007.

[5]IHO Standards for Hydrographic Surveys, Special Publication No.44 [S].5th.International Hydrographic Bureau, 2008.

[6]Calder B, Mayer L A.Robust Automatic Multi-Beam Bathymetric Processing [C].U.S.Hydrographic Conference.Norfolk, VA, USA: 2001.

[7]张孝令, 刘福升.贝叶斯动态模型及其预测 [M].济南: 山东科学技术出版社, 1992.

[8]杨元喜.自适应动态导航定位 [M].北京: 测绘出版社, 2006.

[9]Vásquez M E.Tuning the CARIS implementation of CUBE for Patagonian Waters [D].New Brunswick, Canada: University of New Brunswick, 2007.

[10]柴洪洲, 崔岳.动态系统的抗差Kalman滤波及其影响函数 [J].中国惯性技术学报, 2002, 10(3): 26-30.

[11]王海栋, 柴洪洲, 翟天增, 等.多波束测深异常的两种趋势面检测算法比较 [J].海洋通报, 2010, 29(2): 182-186.

[12]Mallace D, Robertson P.Alternative Use of CUBE: How to Fita Square Pegin a Round Hole [C].U.S.Hydrographic Conference.Norfolk, Virginia: 2007.

Research on multibeam bathymetry data automatic processing based on CUBE algorithm

WANG Hai-dong1,2，CHAI Hong-zhou1,3

（1.Institute of Surveying and Mapping, Information Engineering University, Zhengzhou 450052, China; 2.Navy Press, Tianjin 300450, China; 3.Naval Institute of Hydrographic Surveying and Charting, Tianjin 300061, China）

The CUBE algorithm in automatic processing multibeam bathymetry data is introduced in detail by its model construction, multiple estimations of grid node and the rules of selecting best available estimation.The efficiency of multiple estimations is analyzed intensively, and the algorithm is implemented using multibeam real data.The Robust Kalman filter is presented to improve the CUBE algorithm.The improvement of the algorithm is compared by the experiment of synthetic data, and its necessity is showed.

multibeam bathymetry; CUBE algorithm; robust estimation; Kalman filter; outlier detection; regular square grid

P229

A

1001-6932(2011)03-0246-06

2010-09-27；收修改稿日期：2011-02-24

中国博士后科学基金项目 (20080431342)。

王海栋 ( 1983－ )，男，硕士，主要从事测量数据处理理论与方法研究。

柴洪洲，教授。电子邮箱：chaihz1969@yahoo.com.cn。